离散数学【集合论】备考小结

一、集合

1、集合的基本概念

2、子集

子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。
符号语言：若∀a∈A，均有a∈B，则A⊆B。

3、幂集

• 幂集是指一个集合的所有子集的集合
• 有n个元素形成的集合的幂集共有2的n次方个元素,而且每一个元素都是一个集合.

例如:
集合A={a，b，c} 空集是每个集合的子集，
所以A的幂集为{∅，{a}，{b}，{c}，{a，b}，{a，c}，{b，c}，{a，b，c}}，

二、二元关系

1、定义，条件，性质

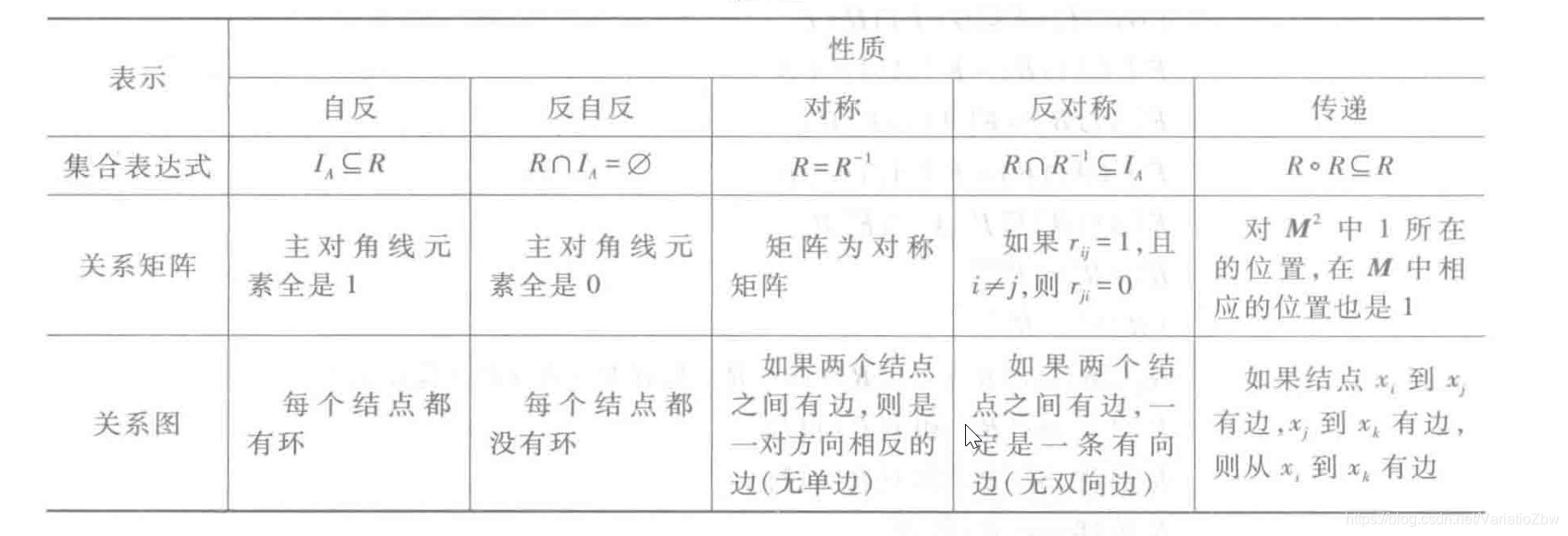
2、关系的基本运算

3、闭包问题

4、等价关系与划分

例题1【等价关系的划分】：

例题2【商集如何求？】：

A={a,b,c,d,e,f}={某大学宿舍的大学生}；R是A上的同乡关系（不难证明同乡关系是等价关系），若a,b是北京人，c是广东人，d,e,f南京人，则R={(a,a)(a,b)(b,a)(b,b)(c,c)(d,d)(d,e)(d,f)(e,d)(e,e)(e,f)(f,d)(f,e)(f,f)}.A中各元素关于R的等价类分别是：
[a]R=[b]R={a,b}；
[c]R={c}；
[d]R=[e]R=[f]R={d,e,f}；
A关于R的商集A/R={[a]R,[c]R,[d]R}={{a,b},{c},{d,e,f}}.

5、偏序关系与偏序集

例题：

三、函数

在数学定义中，单射、满射和双射是指根据其定义域和陪域的关联方式所区分的三类函数。

• 单射：指将不同的变量映射到不同的值的函数。
• 满射：指陪域等于值域的函数。即：对陪域中任意元素，都存在至少一个定义域中的元素与之对应。
• 双射（也称一一对应或一一映射）：既是单射又是满射的函数。直观地说，一个双射函数形成一个对应，并且每一个输入值都有正好一个输出值以及每一个输出值都有正好一个输入值。 （在一些参考书中，“一一”用来指双射，但是这里不用这个较老的用法。）

1、单射，满射，双射的区别