HDU3966【树链剖分】。

最新推荐文章于 2020-04-11 21:33:29 发布

VecSun

最新推荐文章于 2020-04-11 21:33:29 发布

阅读量945

点赞数

分类专栏：数据结构文章标签：树链剖分线段树

本文链接：https://blog.csdn.net/VecSun/article/details/48938777

版权

数据结构专栏收录该内容

5 篇文章 0 订阅

订阅专栏

* 关于树的拆分：*
看了很多资料终于明白一点了，稍微做一下总结。
首先我们应该知道树的拆分分是用来做什么的：
所谓拆分就是把一颗树状结构拆分成线性的结构，然后就可以用树状数组和线段树维护路径，把每次更新或者查询的复杂度做操控制在O（NlogN）左右。

树的拆分方式貌似有很多种，比如最简单的DFS序, 记录的是每个节点u以及u的所有子树的在内的线性标号，即区间【begin_order[u]， end_order[u]】。用于更新或者查询结点的所有子树的情况，即适用于树上的点查询和更新。

void DfsOrder(int u, int f)
{
    begin_order[u] = cnt ++; 
    for(int i = head[u]; i + 1; i = edges[i].next)
    {
        int v = edges[i].v;
        if(v != f)
            DfsOrder(v, u);
    }
    end_order[u] = cnt;
}

当然，如果是要用到更新或者查询树上的每条路径，DFS序显然就不适用了，这时候，要用到一种更为复杂的拆分方式：树链剖分。

首先，要理解这部分几个重要的量和定义：
1.size[u]：以u点为根的节点的数量，即子节点的数量。

2.重儿子和轻儿子。重儿子即与u直接相连的儿子中size最大的那个儿子。每个节点最多有一个重儿子，其余为轻儿子。

3.重链和轻链。一个节点u，与其重儿子相连的边为重链，其余为轻链。

4.其他需要用到的量：
dep[u] :节点的深度。根节点一般标为1。
top[u] :u所在重链中深度最浅的节点。
par[u] :u点的父节点。
pos[u]:树上节点u线段化后在线段上的位置
son[u]:u节点的重儿子。

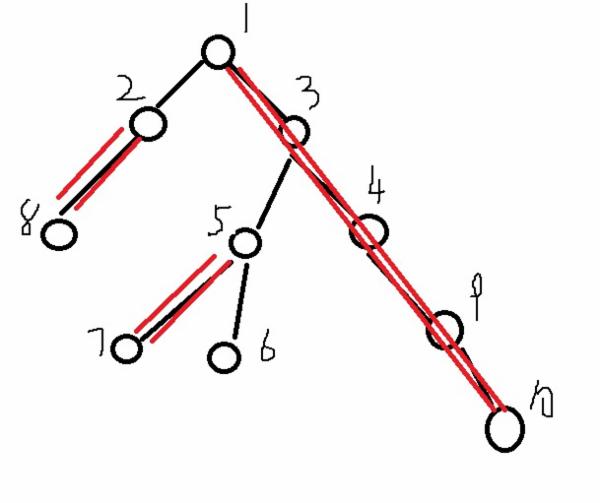
由以上可以知道，对于一个轻儿子，也可能连出他自己的一条重链，如下图中的2号结点。

这样剖分有这样两条性质：

(1)轻边(u,v)中，size[v] <= size[u] / 2；

(2)从根到某一点的路径上，不超过logn条轻边和不超过logn条重路径。

而重链上的路径可以直接更新，所以就这样把本来DFS遍历O(n)的复杂度降到了logN。

然后树链剖分的具体做法就是：
1. 一遍DFS或BFS先求出size、dep、par三个量。

void DfsInit(int u, int f, int d)//u为当前节点，f为u的父节点，d是当前节点的深度。
{
    par[u] = f;
    dep[u] = d;
    son[u] = 0;
    size[u] = 1;
    for(int i = head[u]; i + 1; i = edges[i].next)
    {
        int v = edges[i].v;
        if(v == f) continue;
        DfsInit(v, u, d + 1);
        size[u] += size[v];
        if(size[v] > size[son[u]]) // 如果当前子节点的size比之前算出来的son的size还要大，哪么son改为当前子节点。
             son[u] = v;
    }
}

2.第二遍DFS求出top和pos。

void DfsFinish(int u, int f, int r) // r是当前重链深度最小的节点，即重链的top节点
{
    top[u] = r;
    pos[u] = P_cnt ++; // P_cnt是节点拆分成线性结构中的位置
    if(son[u]) //如果有重链，则先标重链
        DfsFinish(son[u], u, r);
    for(int i = head[u]; i + 1; i = edges[i].next)
    {
        int v = edges[i].next;
        if(v == f || v == son[u])
            continue;
        DfsFinish(v, u, v); //标轻链
    }
}

到此为止剖分就结束了，剩下的就是如何使用你所剖分的链了。
下面我就结合下图来说一下。

转自BLADEVIL

1.比如要更新3 - 9这条路径上的节点。
分别找到3和9的top，记为t1 和 t2，如果t1 == t2,那么从dep[7]和 dep[9],中选择小的作为更新区间【L， R】的L，剩下一个作为R，这里更新可以写成: Update(pos[3], pos[9])。

2.如果更新的区间不在一条重链上，比如区间7 - 9。
首先，记 L = 7和R = 9。 L , R 的top分别为t1 和 t2。
(同样要依据dep来确定L 和 R，即选择深度较深的节点作为L，下面叙述中省略，详见代码)
接下来是个迭代的过程：
判断t1 == t2。这里不相等，哪么：
(1). 更新L - t1区间。
(2). 另L = par[t1], t1 = top[par[L]]。这里显然L变为3，t1变为1。
继续迭代，直到 t1 == t2. 然后说明现在就剩下l和r在一条重链上的子区间还没更新了，然后更新之。
完成。

void CompleteUpdate(int l, int r)
{
    int t1 = top[l], t2 = top[r];
    while(t1 != t2)
    {
        if(dep[l] < dep[r]) //选择较深的节点
        {
            swap(l, r);
            swap(t1, t2);
        }
        Update(pos[t1], pos[l]);
        l = par[t1];
        t1 = top[l];
    }
    if(dep[l] > dep[r])
        swap(l, r);
    Update(pos[l], pos[r]);
}

树链剖分的讲解就到此了，下面是这一题的代码， G++会MLE， C++
AC。 Orz

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int size_max = 50010;
int N, M, P, E_cnt, P_cnt, ans;
int top[size_max];
int dep[size_max];
int son[size_max];
int sve[size_max];
int wei[size_max];
int par[size_max];
int pos[size_max];
int head[size_max];
int size[size_max];
struct Edge
{
    int u, v;
    int next;
}edges[size_max];

struct SegTree
{
    int l, r;
    int lazy;
}seg[size_max << 3];

void init()
{
    E_cnt = 0;
    P_cnt = 0;
    memset(head,-1,sizeof(head));
    memset(size,0,sizeof(size));
    memset(pos,0,sizeof(pos));
}

void addEdge(int u, int v)
{
    edges[E_cnt].u = u, edges[E_cnt].v = v;
    edges[E_cnt].next = head[u];
    head[u] = E_cnt ++;

    edges[E_cnt].u = v, edges[E_cnt].v = u;
    edges[E_cnt].next = head[v];
    head[v] = E_cnt ++;
}

void dfs_init(int u, int f, int d)
{
    par[u] = f;
    dep[u] = d;
    son[u] = 0;
    size[u] = 1;
    for(int i = head[u]; i + 1; i = edges[i].next)
    {
        int v = edges[i].v;
        if(v == f) continue;
        dfs_init(v, u, d + 1);
        size[u] += size[v];
        if(size[v] > size[son[u]])
            son[u] = v;
    }
}

void dfs_pos(int u, int f)
{
    top[u] = f;
    pos[u] = ++P_cnt;
    if(son[u]) dfs_pos(son[u], f);
    for(int i = head[u]; i + 1; i = edges[i].next)
    {
        int v = edges[i].v;
        if(v == par[u] || v == son[u]) continue;
        dfs_pos(v, v);
    }
}

void build(int l, int r, int index)
{
    seg[index].l = l;
    seg[index].r = r;
    seg[index].lazy = 0;

    if(l == r)
    {
        seg[index].lazy = sve[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, index << 1);
    build(mid + 1, r, index << 1 | 1);
}

void update(int l, int r, int index, int c)
{
    if(l <= seg[index].l && seg[index].r <= r)
    {
        seg[index].lazy += c;
        return;
    }
    if(seg[index].lazy)
    {
        seg[index << 1].lazy += seg[index].lazy;
        seg[index << 1|1].lazy += seg[index].lazy;
        seg[index].lazy = 0;
    }
    int mid = (seg[index].l + seg[index].r ) >> 1;
    if(mid >= r)
    {
        update(l, r, index << 1, c);
    }
    else if(l > mid)
    {
        update(l, r, index << 1 | 1, c);
    }
    else
    {
        update(l, mid, index << 1, c);
        update(mid + 1, r, index << 1|1, c);
    }
}

void query(int pos, int index)
{
    if(seg[index].l == pos && seg[index].r == pos)
    {
        ans = seg[index].lazy;
        return;
    }
    if(seg[index].lazy)
    {
        seg[index << 1].lazy  += seg[index].lazy;
        seg[index << 1|1].lazy += seg[index].lazy;
        seg[index].lazy = 0;
    }
    int mid = (seg[index].l + seg[index].r) >> 1;
    if(mid >= pos)
        query(pos, index << 1);
    else
        query(pos, index << 1|1);
}

void get_update(int l, int r, int c)
{
    while(top[l] != top[r])
    {
        if(dep[top[l]] < dep[top[r]])
        {
            swap(l ,r);
        }
        update(pos[top[l]], pos[l], 1, c);
        l = par[top[l]];
    }
    if(dep[l] > dep[r])
        swap(l , r);
    update(pos[l], pos[r], 1, c);
}

void dfs()
{
    dfs_init(1, 0, 1);
    dfs_pos(1 , 1);
}
int main(int argc, char const *argv[])
{
    while(~scanf("%d %d %d",&N,&M,&P))
    {
        init(); int u, v, c;
        for(int i = 1; i <= N; i ++)
        {
            scanf("%d",&wei[i]);
        }
        for(int i = 1; i <= M; i ++)
        {
            scanf("%d %d",&u,&v);
            addEdge(u, v);
        }
        dfs();
        for(int i = 1; i <= N; i ++)
        {
            sve[pos[i]] = wei[i];
        }
        build(1, N, 1);
        char qus[5];
        for(int i = 0; i < P; i ++)
        {
            scanf("%s", qus);
            if(qus[0] == 'I')
            {
                scanf("%d %d %d",&u,&v,&c);
                get_update(u, v, c);
            }
            else if(qus[0] == 'D')
            {
                scanf("%d %d %d",&u,&v,&c);
                get_update(u, v, -c);
            }
            else
            {
                scanf("%d",&u);
                query(pos[u], 1);
                printf("%d\n",ans);
            }
        }
    }
    return 0;
}