题意:给n个点m条边,选定一个区域使边数与点数的比值最大。
证明见胡伯涛《最小割模型在信息学竞赛中的应用》。
不过证明中有错误(一个系数),着实被坑了一把...在P24页下面那段证明中,正确的证明在何亮的课件《图论杂项》中给出。传送门
好在这段只是证明解题思路, 后面的建边与求解又是单独的一块, 所以并不影响整篇论文的正确性...(这么多年怎么就没哪位大牛纠正一下..这不贻害后人么....)
在P25页中,给出了建图的方式,并在26页中给出了证明。
至于为什么这么建...额...木有讲...难道大牛们都是猛然间顿悟出怎么建的图然后才证明...?
解题方法:分数规划,还是论文上的东西,包括主算法和改进算法都在上面,我就只讲解题方法了。
先设定一个足够大的常数U (U=m 就足够了)
二分枚举猜测值,对于每个猜测值g重构图,
h(g)=(U*n-最小割) / 2.
建图:
对于每个点Vi,建c(S,Vi)=U, c(Vi,T)=U + 2*g - Di (Di为Vi的度)
对于原图的每条边(u,v),建c(u,v)=1,c(v,u)=1
在每次建图中,唯一发生变化的边是Vi到T的边,最小割也因为这些边的变化而变化
随着猜测值g的递增而递增,直到上限U*n (割掉所有从s到Vi的边)
所以最小割与g的图像时这样的
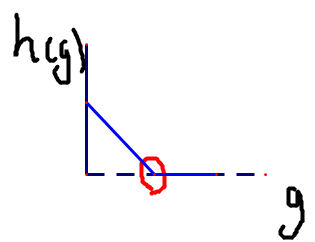
而h(g)与g之间的图像时这样的
红色圈起来的点即为我们要求的点,也就是h(g)为0时的值。
然后用这个g值求一次最小割,按残余流量进行遍历,能遍历到的点即为要输出的点。(至于为什么,我在2987中给出了类似的证明)
贴代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <cmath>
using namespace std;
#define FOR(i,l,r) for(int i=(l);i<=(r);++i)
#define REP(i,n) for(int i=0;i<(n);++i)
#define DSC(i,r,l) for(int i=(r);i>=(l);--i)
#define eps 1e-5 //精度
#define N 110
#define M 3000
#define INF 1e8
struct
{
int to,next;
double c;
}edge[M];
int head[N],level[N],ip;
int que[N],degree[N],ans[N];//degree记录度,ans记录最后能遍历到的点
bool makelevel(int s,int t)
{
memset(level,0,sizeof(level));
int iq=0;
que[iq++]=s;
level[s]=1;
int top;
for(int i=0;i<iq;i++)
{
top=que[i];
if(top==t) return 1;
for(int k=head[top];k!=-1;k=edge[k].next)
{
if(!level[edge[k].to]&&edge[k].c>eps)
{
que[iq++]=edge[k].to;
level[edge[k].to]=level[top]+1;
}
}
}
return 0;
}
double dfs(int now,double maxf,int t)
{
if(now==t) return maxf;
double ret=0,c;
for(int k=head[now];k!=-1;k=edge[k].next)
{
if(edge[k].c>eps&&level[edge[k].to]==(level[now]+1))
{
c=dfs(edge[k].to,min(maxf-ret,edge[k].c),t);
edge[k].c-=c;
edge[k^1].c+=c;
ret+=c;
if(fabs(ret-maxf)<eps) return ret;
}
}
if(!ret) level[now]-=2;
return ret;
}
double dinic(int s,int t)
{
double ans=0;
while(makelevel(s,t)) ans+=dfs(s,INF,t);
return ans;
}
void add(int u,int v,double c,double f) //有向边f为0 ,否则为 c
{
edge[ip].to=v;edge[ip].c=c;edge[ip].next=head[u];head[u]=ip++;
edge[ip].to=u;edge[ip].c=f;edge[ip].next=head[v];head[v]=ip++;
}
//前面为模板,不用看了
struct
{
int x,y;
}f[M];
void build(double mid,int n,int m)
{
memset(head,-1,sizeof(head)); ip=0;
REP(i,m) add(f[i].x,f[i].y,1,1);
FOR(i,1,n)
{
add(0,i,(double)m,0);
add(i,n+1,(double)m + 2.0*mid -(double)degree[i] ,0 );
}
}
void dfs1(int pos,int &num) //最后遍历求要选的点
{
level[pos]=1;
ans[num++]=pos;
for(int p=head[pos];p!=-1;p=edge[p].next)
{
if(edge[p].c>0 && !level[ edge[p].to ] )
dfs1(edge[p].to,num);
}
}
int main()
{
int n,m;
while(cin>>n>>m)
{
if(m==0)
{
cout<<1<<endl<<1<<endl;
continue;
}
memset(degree,0,sizeof(degree));
REP(i,m)
{
scanf("%d%d",&f[i].x,&f[i].y);
degree[ f[i].x ]++;
degree[ f[i].y ]++;
}
double l=1.0/n,r=(double)m,mid=(l+r)/2.0,temp;
while(r-l>1.0/n/n)//胡伯涛的论文给出了证明,不同解之间误差的精度不超过1/(n*n)
{
build(mid,n,m); //每次二分要重构图
temp=((double) n*m - dinic(0,n+1))/2.0;
if(temp>eps) l=mid;
else r=mid;
mid=(l+r)/2.0;
}
build(l,n,m); //用mid值建图容易wa,因为你此时的mid不一定满足h(mid)>eps,但是l一定是满足的
dinic(0,n+1);
int num=0;
memset(level,0,sizeof(level));//重新利用一下这个数组,记录点是否被遍历过
dfs1(0,num);
sort(ans,ans+num);
cout<<num-1<<endl;
FOR(i,1,num-1) printf("%d\n",ans[i]);
}
return 0;
}








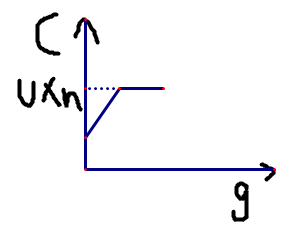














 1165
1165

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








