Java API 1.8源码--【集合类 collection】

集合：

     集合就是管理其他对象的一种对象。集合对象定义了一些特定的方法，来管理 访问它里面的包含的元素。（它包含的元素就是他管理的那些对象）

        stack   =  new   Stack  < Integer  >();   

        //为什么用非要麻烦的写 Integer转来转去  而不是 int 呢？ 因为集合类规定类是存对象的，不能存 int这些基本类型。所以涉及到集合类存数据都是包装类存进去的。

            

集合的使用者:

     是其他的对象，这些使用者只能通过这个集合类的这些方法才能跟给集合进行交互(访问、增删)。也就是说，集合类给使用集合的类提供了接口。

集合分为两大类，一种是线性的，一种是非线性的。

• 线性结构：是按照直线挨个排列的方式组织集合里的那些元素们。
• 非线性结构：按照层次结构或者网状结构甚至没有结构来存储管理集合里的元素们

---

---

【Stack类 】 

【栈——也叫堆栈】

• • 栈是一种线形集合，元素是线性排列
  • 栈里面元素的添加和删除都是在栈顶一端进行，
  • 先进后出FILO的方式——也就是说，放入栈的顺序和出来的顺序恰好是相反的。比如说字符串的反转 和 后缀表达式计算

【javaAPI 1.8 里成熟的stack类】：

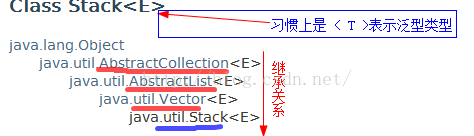
• 可被序列化  Serialized 
• last-in-first-out (LIFO) stack of object
• 构造器Constructors
  • Stack( )      //Creates an empty Stack.
  
  

  ---

  
  
  Stack常用的 方法：

  • 把一个元素添加到栈顶 
    •   public E push( E item ) {
              addElement (item );
             return item ;
          }
  • 把一个元素从栈顶移除—— synchronized 线程安全
    • public synchronized E pop() {
              E obj;
             int  len = size ();
             obj = peek ();
             removeElementAt (len - 1 );
              return obj ;
          }
  • 查看栈顶的元素—— synchronized 线程安全
    •    public synchronized E peek()  {
              int len = size ();
              if ( len == 0 )
                  throw new EmptyStackException();
              return elementAt( len - 1 );
          }
  • 判断栈是否为空
    •   public boolean empty() {
              return size() == 0 ;
          }
  • 计算栈里的元素个数int size()
  • 查找某个对象在栈里的位置 
    •     public synchronized int search( Object o ) {
              int i = lastIndexOf (o );
              if ( i >= 0 ) {
                  return size() - i;
              }
              return - 1 ;
          }
      

  
  

  ---

  
  

  ---

  Stack 异常：

  • 压入元素的时候栈已经满了。
    • 实际上逻辑理论来讲栈永远不可能满。但是实际的机器的内存是有限的。有可能堆空间分配光了。出现异常。
  • 弹出栈是为空
    • 弹完了还pop那就是emptystackException。
    • 多线程时候，不同线程造车都执行pop操作，线程冲突。

  
  

  • 你的业务逻辑本身的一些异常。

  
  

  
  

  
  

  
  

  
  

  
  
  【栈的使用----逆波兰表达式--简单】
  
  

  import java.util.Scanner;
  import java.util.Stack;
  
  
  /**
   * 
   * @author 杰
   * 逆波兰表达式(后缀表达式)
   * 
   */
  
  
  public class postfix {
  
  	private final static char ADD='+';   //私有  静态变量所以再加final
  	private final static char SUB='-'; 
  	private final static char MUL='*'; 
  	private final static char DIV='/'; 
  	
  	private Stack<Integer> stack;
  	
  	/**
  	 *构造器  初始化一个栈    存储Interger对象
  	 */
  	
  	postfix(){
  		stack = new Stack<Integer>();
  	}
  	
  	
  	/**
  	 * 把输入的表达式new 一个parser对象。然后利用hasNext()和 next()提取符号token
  	 * 当遇到一个operator 那么opt1和opt2存字符。 注意先弹出opt2 再弹出opt1。然后和表达式parser按字符一起给jisuan.然后把结果压入
  	 * 遇到是数值变成Integer压入栈。
  	 * 
  	 * @param expression  表达式
  	 * @return result 结果
  	 */
  	
  	public int evaluate(String expression) {
  		int opt1,opt2,result = 0;
  		String token;
  		
  		Scanner parser = new Scanner(expression);
  		
  		while(parser.hasNext()){
  			
  			token = parser.next();
  			
  			if(isopertor(token)){
  				opt2 = (stack.pop()).intValue();
  				opt1 = (stack.pop()).intValue();
  				result = jisuan(token.charAt(0),opt1,opt2);
  				
  				stack.push(new Integer(result));
  			}
  			else{
  				stack.push(new Integer(Integer.parseInt(token)));
  			}
  			
  		}
  		return result;
  	}
  
  /**
   * 
   * @param charAt
   * @param opt1
   * @param opt2
   * @return
   */
  	private int jisuan(char charAt, int opt1, int opt2) {
  		
  		int res = 0;
  		
  		switch(charAt){
  		
  		case ADD:
  			res = opt1+opt2;
  			break;
  		case SUB:
  			res = opt1-opt2;
  			break;
  		case MUL:
  			res = opt1*opt2;
  			break;
  		case DIV:
  			res = opt1/opt2;
  			break;	
  		
  		}
  		
  		return res;
  	
  	}
  
  /**
   * 做布尔判断。四个有一个即可判断数操作符。
   * @param token
   * @return
   */
  	private boolean isopertor(String token) {
  
  		return (token.equals("+")||token.equals("-")||token.equals("*")||token.equals("/"));
  		
  	}
  
  	
  }
  

  import java.util.Scanner;
  
  public class test {
  
  	/**
  	 * 读入一个逆波兰表达式postfix expression 然后求值
  	 * read and evaluates postfix expression
  	 */
  	public static void main(String[] args) {
  		
  		String expression = null;
  		
  		Scanner in = new Scanner(System.in);
  		postfix  demo = new postfix();
  		
  		//插入一个正确的逆波兰表达式：每个字符之间加个空格，和有效操作符(+-*/%)
  		System.out.println("enter a valid postfix expression:\n\t\t insert a space between each token and with valid operator (+ - * / )");
  		System.out.println("EG: 5 4 + 3 2 1 - + *) ");
  		
  		expression = in.nextLine();
  		
  		System.out.println("\n"+"expression result="+demo.evaluate(expression));
  		
  		
  		
  		
  		
  	}
  	
  }
  

  
  
  
  
• 可被序列化  Serialized 
• last-in-first-out (LIFO) stack of object
• 构造器Constructors
  • Stack( )      //Creates an empty Stack.