原码一位乘的数值运算

原码一位乘的数值运算

今天看原码的乘法，总感觉整个过程被讲复杂了。
刚好在这里总结一下。

因为我看的教材时唐朔飞版的计组，所以很多就引用书上的内容来写一下我自己的理解，感觉能比较容易理解，至少没那么抽象。

首先是笔算乘法。这个很简单，看一下就会发现，这其实和我们小学时学十进制乘法写竖式没什么太大区别，就是下面的数从最末尾开始依次与上面的数相乘然后相加。（见下图）

这里是引用

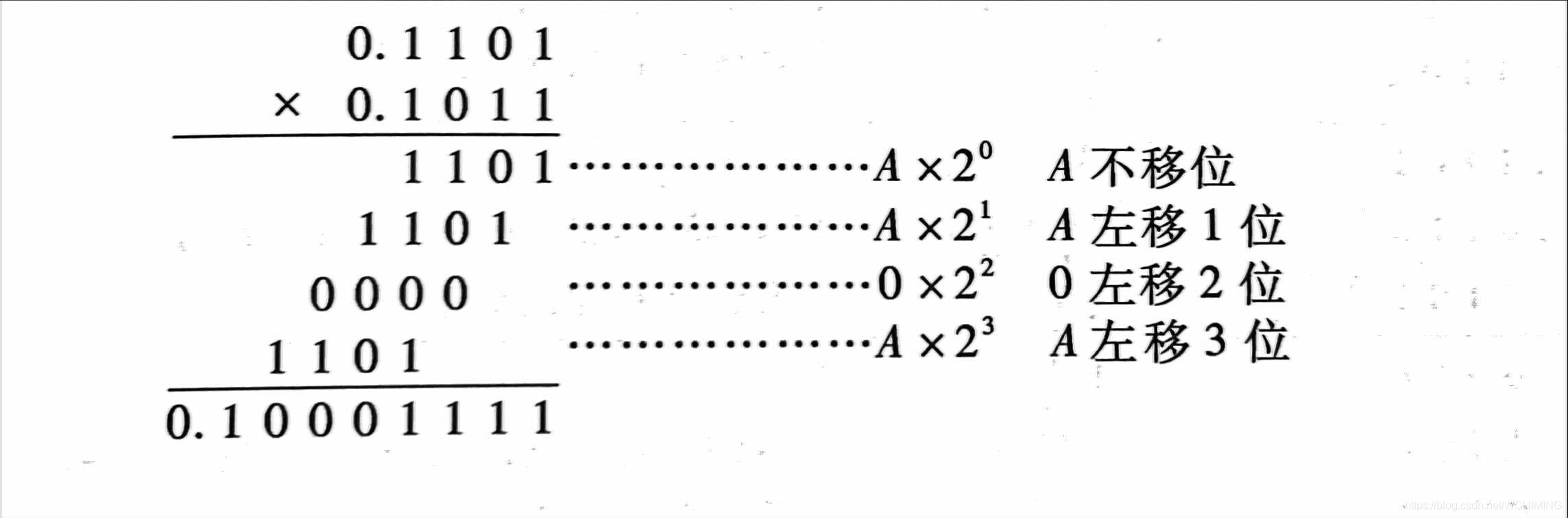
但是这种办法在计算机中是不合适的，无论是从算法还是硬件实现来说。因此需要对算法进行改进，让其符合计算机的工作流程。(改进后的算式如下图)

那么改进之后的算法其实算是利用了因式分解，将一个二进制的小数分为了0.1、0.01、0.001、0.0001……（当然因为有的位上是零，所以是0.000……）；然后从小到大提取两两之间的公因子，让他们重新组合在一起。这样就把乘法运算用加法和移位成功解决。

这部分还是书上的描述准确就是：

从初始值为0开始，对式做分步运算，则：

第一步：被乘数加零 A+0=0.1101+0.0000=0.1101
第二步：右移一位得新的部分积 2^-1(A+0)=0.01101
第三步：被乘数加部分积 A+2^-1(A+0)=0.1101+0.01101=1.00111
第四步：右移一位，得到新的部分积 2^-1 [A+2^-1(A+0)]=0.100111

在这个改进过后的算法中我们在看书上对分布运算的描述时请直接看着最后一步，就很明显就是从内向外一层层进行计算，图中的运算过程其可以看作是对这个算法的一个验证。

要注意的是，在第三步中的被乘数A其实是1A，相对应的，如果相对应的位上是0，那么就是0A（即使什么也没有也要写上，这时的你就是莫得感情的机器），加被乘数的步骤数与乘数位数是相同的，也就是乘数有多少位，你就要算多少次。书中后面的几步中其实有，可以自行翻阅书籍。

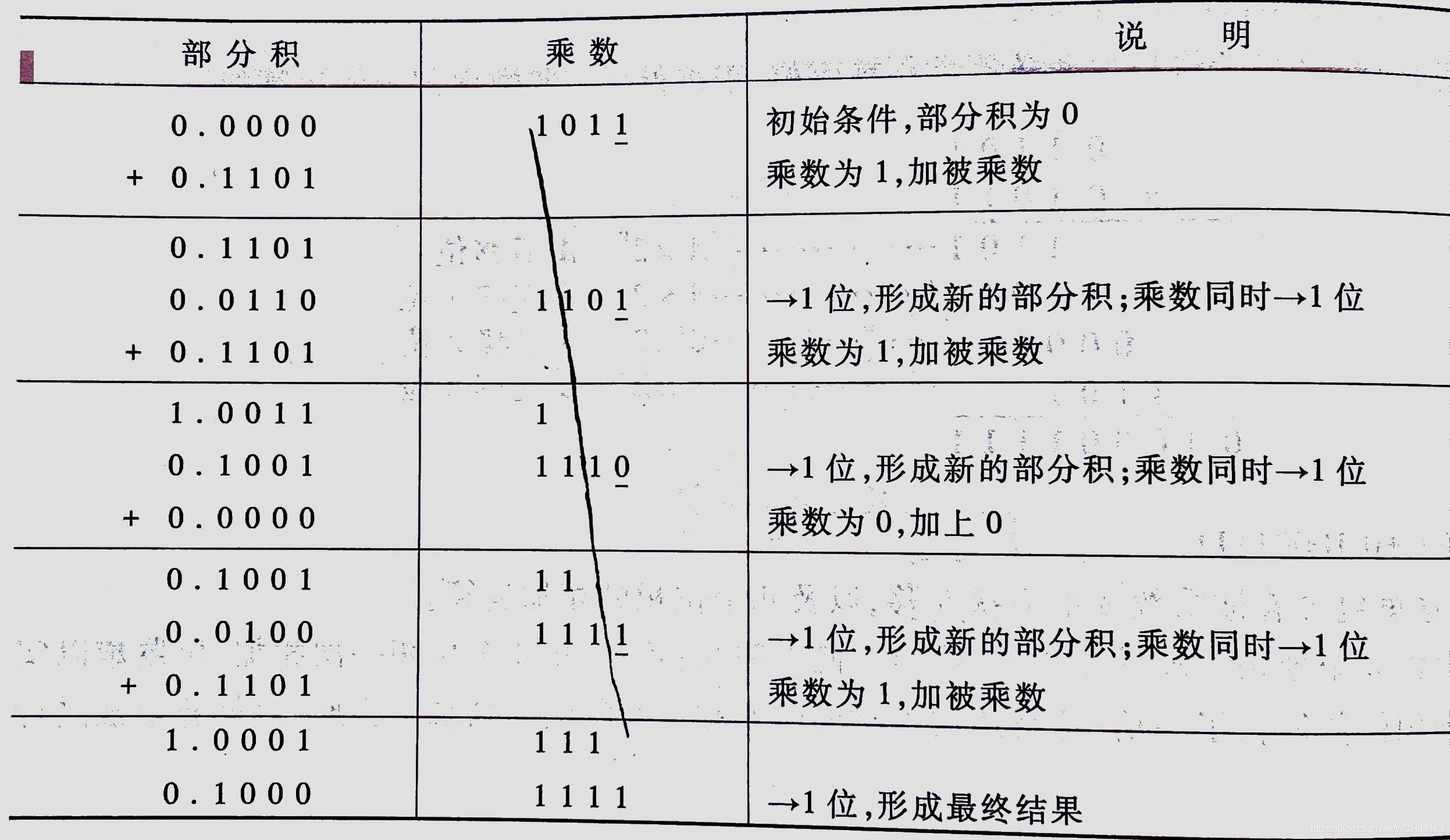
书中的这张表格列出了全部的运算过程，但。。。。。。我确实一下子没看懂这到底表示了什么。

上述运算过程可归纳如下：
1.乘法运算可用 加法来实现，两个4位数相乘，总共需要进行4次加法运算和4次移位。
2.由乘数的末位值确定被乘数是否与原部分积相加，然后右移一位，形成新的部分积；同时，乘数也右移一位，由次低位作新的末位，空出最高位放部分积的最低位
。
3.每次做加法时，被乘数仅仅与原部分积的高位相加，其低位被移至乘数所空出的高位位置。 计算机很容易实现这种运算规则 。 用一个寄存器存放被乘数，一个寄存器存放乘积的高位
，一个寄存器存放乘数及乘积的低位，再配上加法器及其他相应电路，就可组成乘法器。又因加去只在部分积的高位进行，故不但节省了器材，而且还缩短了运算时间。

其实到这里还是不够明白，我也是云里雾里，但直到看到了原码一位乘的硬件配置。
但在这之前还是要把前置条件简单说一下。

因为是原码一位乘，因此在运算时使用的是原码，简单来说就是符号位和数值位各算各的，算完了再合到一起。
符号位采用异或运算，和十进制差不多。

而数值部分：
数值部分因为去掉了符号位，因此是对他们的绝对值进行运算，就是采用刚刚改进的算法。而且因为乘积是两绝对值相乘的结果，所以这里的右移操作都是逻辑右移。

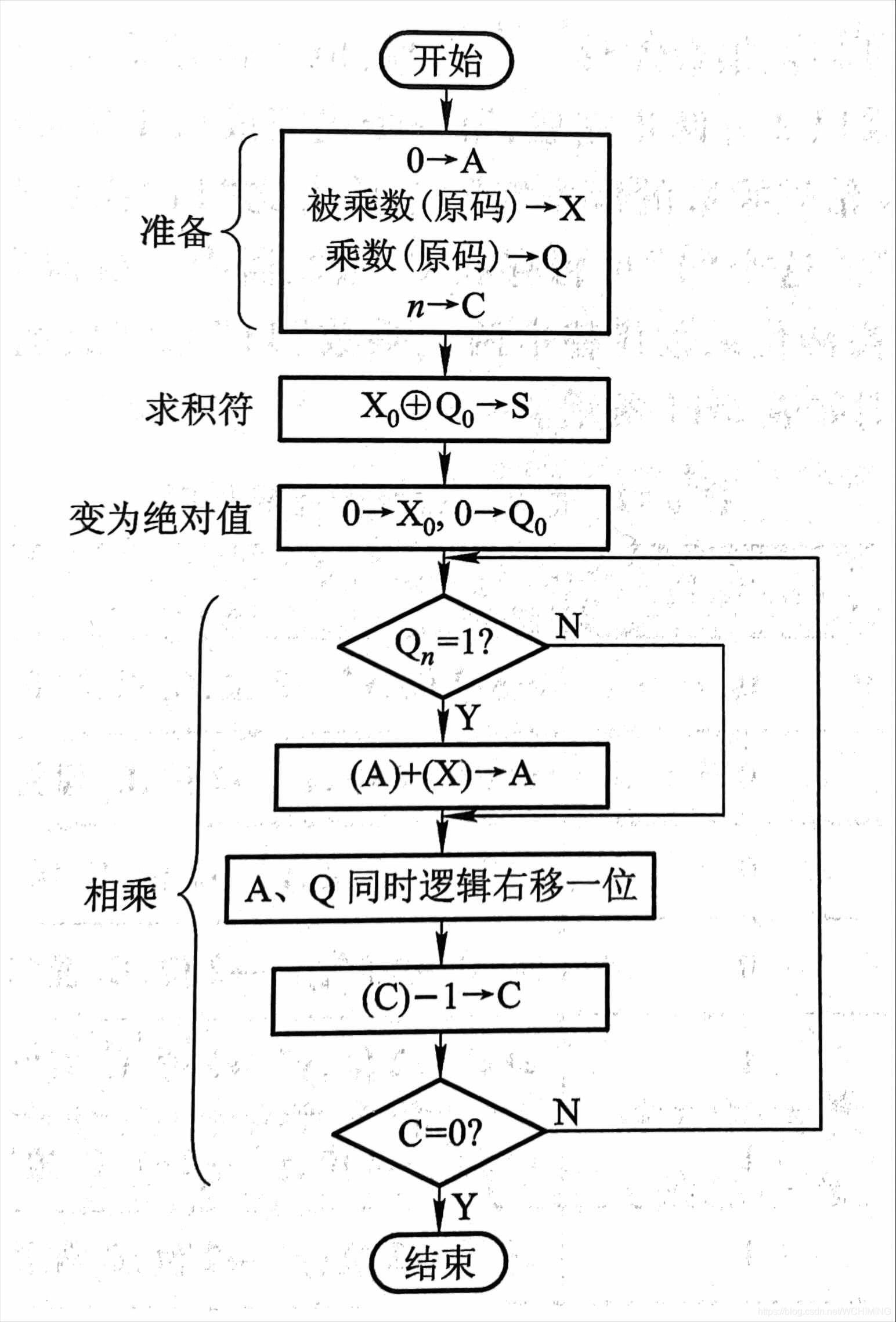
最终帮助我完全理解这个乘法运算过程的来了，就是实现原码一位乘运算基本硬件配置框图。（见下图）

这里先说明一下：
A、X、Q均为n+1位的寄存器（n为乘数被乘数的位数），其中X存放被乘数的原码，Q存放乘数的原码。
移位和加控制电路受Qn的控制（当Qn=1时，A和X内容相加后，A、Q右移一位；当Qn=0时，只作A、Q右移一位的操作）。
计数器C用于控制逐位相乘的次数。
S存放乘积的符号。
GM为乘法标记。

其实到这里就很明白了，A和Q其实是可以看作相通的。

具体操作就是，A在最开始被清零，根据Qn的值决定是否把X中的被乘数塞入A，然后A、Q进行右移操作，也就是An变成Q0,其他的也同样右移。接着重复加粗部分的步骤n次，就可以得出结果。

这一过程实际上就是还原了最开始笔算乘法的算法，但是计算机不能像人一样一口气加完，最后数一数把小数点点上！但是这个算法就相当与把最开始那张图中的数分步加在一起，同时解决了小数点的问题。

个人认为这一过程很有机械的美感，仿佛看到了步进传送带，从A0一直到Qn。
传送带上一侧放着需要加工的数据（被乘数），另一侧是驱动加工程序的薪柴（乘数），而每一次相加（或者不加）都是对传送带上的数据进行加工。
每一次加工结束，则传送带向后进一格，同时也将薪柴送入锅炉（移位和加控制电路）。
当最后薪柴耗尽，加工也就结束，将传送带上的数据串起来就是最后的成品（乘积）。
当然不要忘记存在S中的包装（符号位）。

最后附上书中的流程图