判断一个数是否为素数

🚀欢迎互三！

目录

1、暴力法：

2、线性筛法：

3、类欧几里得算法：

4、埃氏筛法：

---

在计算机程序中，可以使用以下几种方法来判断一个数是否为素数：

1、暴力法：

遍历 2 到根号 n 的数，判断 n 是否能被它们整除。如果 n 能被任意一个数整除，则 n 不是素数；否则 n 是素数。下面是一个使用暴力法判断素数的 C++ 代码示例：

#include <iostream>
#include <cmath>

using namespace std;

bool is_prime(int n) {
    if (n <= 1) return false;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) return false;
    }
    return true;
}

int main() {
    int n;
    cin >> n;
    if (is_prime(n)) {
        cout << n << " is a prime number" << endl;
    }
    else {
        cout << n << " is not a prime number" << endl;
    }
    return 0;
}

运行结果

2、线性筛法：

使用线性时间复杂度来预处理出小于等于给定数 n 的所有素数，然后判断 n 是否在素数列表中。下面是使用线性筛法判断素数的 C++ 代码示例：

#include <iostream>
#include <cmath>

using namespace std;

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1000000;

bool isPrime[N + 5]; // isPrime[i]表示数字i是否是素数

void linear_sieve(int n) {
    memset(isPrime, true, sizeof(isPrime)); // 初始化，假设所有数字都是素数
    isPrime[0] = isPrime[1] = false; // 0和1不是素数
    for (int i = 2; i <= n; i++) { // 从2开始枚举
        if (isPrime[i]) { // 如果i是素数
            for (int j = i * i; j <= n; j += i) { // 将i的倍数全部标记为合数
                isPrime[j] = false;
            }
        }
    }
}

int main() {
    int n;
    cin >> n;
    linear_sieve(n); // 求出小于等于n的素数
    for (int i = 0; i <= n; i++) {
        if (isPrime[i]) {
            cout << i << " ";
        }
    }
    cout << endl;
    return 0;
}

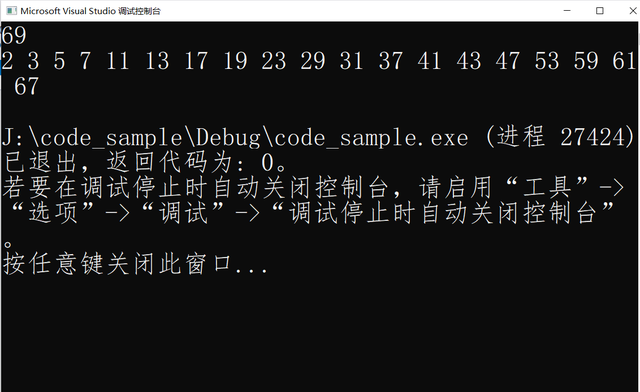
运行结果

3、类欧几里得算法：

在数论中，可以使用类欧几里得算法来判断一个数是否为素数。根据费马小定理（Fermat's little theorem），对于所有大于 2 的正整数 n，如果存在一个数 a，使得 a^(n-1) ≡ 1 (mod n)，则 n 为素数。

因此，我们可以使用类欧几里得算法来快速计算 a^(n-1) mod n 的值，如果结果为 1，则 n 为素数；否则 n 不是素数。下面是使用类欧几里得算法判断素数的 C++ 代码示例：

#include <iostream>
#include <cmath>

using namespace std;

int mod_pow(int a, int b, int m) {
  int res = 1;
  a %= m;
  while (b > 0) {
    if (b & 1) res = res * a % m;
    a = a * a % m;
    b >>= 1;
  }
  return res;
}

bool is_prime(int n) {
  if (n <= 1) return false;
  if (n <= 3) return true;
  int d = n - 1;
  while (d % 2 == 0) d /= 2;
  for (int a : {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}) {
    if (n == a) return true;
    if (mod_pow(a, d, n) == 1) continue;
    int r = d;
    while (r < n - 1 && mod_pow(a, r, n) != n - 1) r *= 2;
    if (r >= n - 1) return false;
  }
  return true;
}

int main() {
  int n;
  cin >> n;
  if (is_prime(n)) {
    cout << n << " is a prime number" << endl;
  } else {
    cout << n << " is not a prime number" << endl;
  }
  return 0;
}

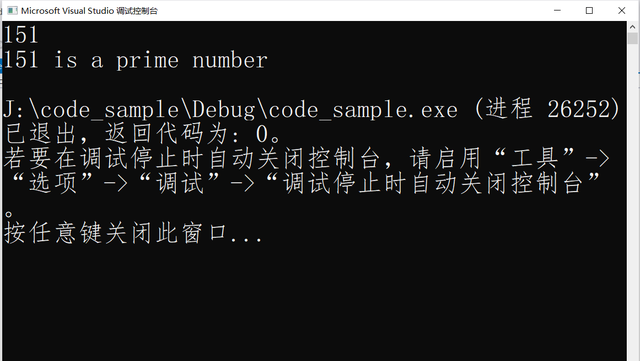
运行结果

4、埃氏筛法：

埃氏筛法（Sieve of Eratosthenes）是一种用于预处理小于等于给定数 n 的所有素数的算法。该算法的基本思想是，使用一个布尔数组来存储小于等于 n 的数是否为素数，然后逐个遍历这些数，并根据它们是否为素数来更新数组中其他数的状态。下面是使用埃氏筛法判断素数的 C++ 代码示例：

#include <iostream>
#include <cmath>

using namespace std;

int mod_pow(int a, int b, int m) {
  int res = 1;
  a %= m;
  while (b > 0) {
    if (b & 1) res = res * a % m;
    a = a * a % m;
#include <iostream>
#include <cstring>
#include <cmath>

using namespace std;

const int N = 1000000;

bool is_prime[N + 5];

void sieve() {
  memset(is_prime, true, sizeof(is_prime));
  is_prime[0] = is_prime[1] = false;
  for (int i = 2; i <= N; i++) {
    if (is_prime[i]) {
      for (int j = 2 * i; j <= N; j += i) {
        is_prime[j] = false;
      }
    }
  }
}

bool check_prime(int n) {
  return is_prime[n];
}

int main() {
  sieve();
  int n;
  cin >> n;
  if (check_prime(n)) {
    cout << n << " is a prime number" << endl;
  } else {
    cout << n << " is not a prime number" << endl;
  }
  return 0;
}

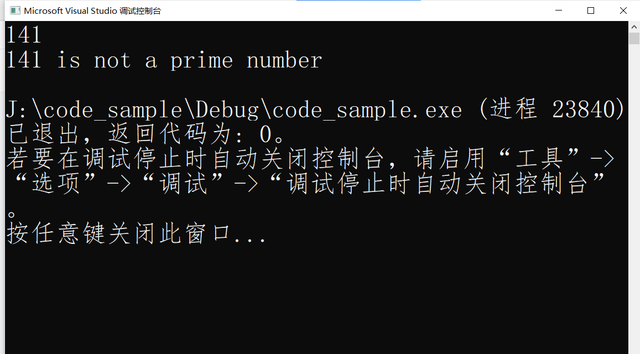
运行结果

以上四种方法都可以判断素数，大家学会了吗？