折半查找:
说明:插入和进制转换用到了 数组的操作,就当对数组进一步了解了。
要求:一定是对有序序列的查找
/*
需求:将一个已知元素插入到一个有序数组中,要求不改变数组顺序,打印元素应该插入数组位置的角标。
思路:1、可以利用折半查找的方式,先定义两个变量,一个初始化0角标,作为最小值,一个初始化为最后一个角标,作为最大值,
再定义一个变量,存储最小值与最大值的一半,也就是中间位置,然后将已知元素与中间值位元素进行比较。
2、如果比中间值元素大,则将最小值变为中间值加1,继续取最小值与最大值的中间值元素与已经元素进行比较,以此反复
3、如果比中间值元素小,则将最大值变为中间值减1,继续取最小值与最大值的中间值元素与已经元素进行比较,以此反复
*/
public class BinarySearch1
{
/***************************
折半查找 Version-1.0
这个折半查找我在写的时候有一点问题,
问题一:if(min>max)这句话的判断不能直接放在开头,因为如果查询的数小于头会报数组越界错误
原因:此时max已经指向-1,所以mid取-1,所以越界了
***************************/
public static int binarySearch1(int key,int arr[])
{
int min = 0;
int max = arr.length-1;
int mid = (min+max)/2;
while(key!=arr[mid])
{
//位置1:
//if(min>max)
//{
// return -1;
//}
mid = (min+max)/2;
if(key>arr[mid])
{
min = mid + 1;
}else if(key<arr[mid])
{
max = mid - 1;
}
if(min>max)
{
return -1;
}
mid = (min+max)/2;
}
return mid;
}
/*
折半查找 version-2.0
这种方法不会出现问题一,因为一旦min>max了,就跳出循环了,不会出现越界问题了
*/
public static int binarySearch2(int key,int arr[])
{
int min = 0;
int max = arr.length-1,mid;
while(min<=max)
{
mid = (min+max)>>>1;
if(key>arr[mid])
{
min = mid + 1;
}else if(key<arr[mid])
{
max = mid - 1;
}else
{
return mid;
}
}
return -1;
}
public static void main(String []args)
{
int arr1[] = {0,3,7,9,11,12,14,70,80,90,100};
int key = 3;//11,100
int y = binarySearch1(key,arr1);
int z = binarySearch2(key,arr1);
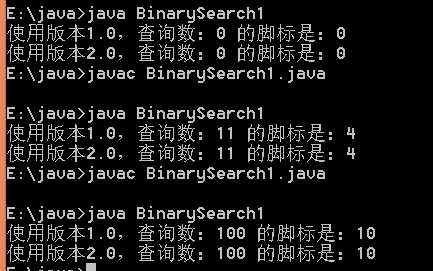
System.out.println("使用版本1.0,查询到的脚标数的脚标是:"+y);
System.out.print("使用版本2.0,查询到的脚标数的脚标是:"+z);
}
}结果是:
折半查找的插入点返回
如果查找的数字是不存在的,我想知道他可以插在那个地方:
先要知道一个概念,如果没有查到想要的数,那么min和max指向哪里?
画图理解二分法插入:
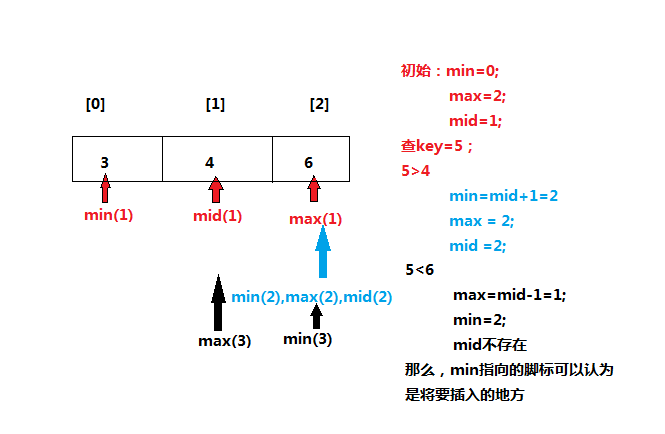
那么根据上面的查找,只需将return -1改为return min;就可以了!
public class BinarySearch1
{
//二分查找法改进为可以找不存在的数的插入点
public static int binarySearch2(int key,int arr[])
{
int min = 0;
int max = arr.length-1,mid;
while(min<=max)
{
mid = (min+max)>>>1;
if(key>arr[mid])
{
min = mid + 1;
}else if(key<arr[mid])
{
max = mid - 1;
}else
{
return mid;
}
}
//修改这里的返回值
return min;
}
public static void main(String []args)
{
int arr1[] = {0,3,7,9,11,12,14,70,80,90,100};
int key = 5;
int z = binarySearch2(key,arr1);
System.out.println("使用版本2.0,查询数:"+key+" 的脚标是:"+z);
int a = Arrays.binarySearch(arr1, key);
System.out.println("使用Arrays下的方法,查找 "+key+" 的脚标是:"+a);
}
}运行:
这里根据java.util.Arrays类的方法binarySearch进行比较,感觉人家写得好啊,我这个找出来的不知道是查到了还是插入点,人家的方法清楚,正数是查到的脚标,负数时将插入的脚标。
优化:将return min;可以改写为return -1-min。结果就和他的一样了。
进制转换
十进制转十六进制:
/*
使用查表法将十进制转换为十六进制
*/
public class ToHex1
{
public static char[] toHex(int num)
{
if(num==0)
{
char []c1 = {'0'};
return c1;
}
//定义一个包含二进制、八进制、十六进制的表
char hex[] = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
//定义一个临时容器
char c[] = {'0','0','0','0','0','0','0','0'};
//定义一个操作数组的指针
int i = c.length;
//利用与低位最大值的方式取出低位,存到临时数组中
while(num!=0)
{
c[--i] = hex[num&15];//--pos倒着往临时容器里存
num = num>>>4;//无条件右移相应位数
}
return c;
}
public static void main(String args[])
{
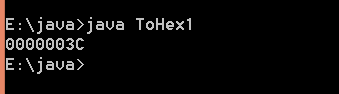
int a = 60;
System.out.print(toHex(a));
}
}结果:
十进制转二进制,八进制,十六进制
将以上方法封装升级,转换成可以重复利用,并可以实现十进制转二进制和八进制:
public class ToHex1
{
//抽象出来的方法,base是“与(&)”的对象,move是移动的位数
public static void convert(int num ,int base,int move)
{
//0比较特殊,需要特殊对待
if(num==0)
{
char []c1 = {'0'};
System.out.print("0");
return;
}
char hex[] = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
char c[] = new char[32];
int i = c.length;
while(num!=0)
{
c[--i] = hex[num&base];
num = num>>>move;
}
for(int j=i;j<c.length;j++)
{
System.out.print(c[j]);
}
}
//转二进制
public static void toBinary(int num)
{
convert(num,1,1);
//换行
System.out.println();
}
//转八进制
public static void toOctal(int num)
{
convert(num,7,3);
//换行
System.out.println();
}
//转十六进制
public static void toHex(int num)
{
convert(num,15,4);
//换行
System.out.println();
}
public static void main(String args[])
{
int a = 60;
System.out.print("数"+a+"对应二进制:");
toBinary(a);
System.out.print("数"+a+"对应八进制:");
toOctal(a);
System.out.print("数"+a+"对应十六进制:");
toHex(a);
}
}运行结果(0和60):
总结:
1.折半查找的思想
2.对折半查找的min和max的理解可以推导出:对不存在数的插入位置的推断。
3.进制转换,“与(&)”的运用,取位操作。


























 576
576

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








