数学题集合1_轻拍牛头难度-CSDN博客

本文链接：https://blog.csdn.net/Water_Sunzhipeng/article/details/141032287

约数个数

约数个数

求一个数的约数的时间复杂度是o(sqrt(n)), 大部分密码都是基于rsa，全乘法简单，分解难，求每个数有多少个数是他的倍数，从1到1e6；看有多少个是他的倍数， n(logn) 106 * log106

2024牛客多校8A题

给定一个序列，求出我们能够生成多少个没有出现过的gcd(x, y),

首先我们如果分解约数，然后查找没出现过的公约数，显然非常麻烦，我们根据能够转化为乘法的性质，反过来枚举假设这个点是生成的gcd，那麽他一定满足，这个数没有出现过，并且任意两个数a1, b1 可以得到gcd(a1/x, b1/x) = 1的，我们枚举最小的点，那么我们是可以推出来的。时间复杂度是 n*logN

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n);
    vector<int> m(1e5 + 10);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        m[a[i]] = 1;
    }
    int res = 0;
    for(int i = 1; i <= 1e5; i++){
        if(!m[i]){
            int t = -1;
            for(int j = 2; j * i <= 1e5; j ++){
                if(m[i * j]){
                    if(t == -1)
                        t = j;
                    else{
                        t = gcd(t, j);
                        if(t == 1)
                            break;
                    }
                }
            }
            if(t == 1)
                res ++;
        }
    }

    if (res % 2 == 1) {
        cout << "dXqwq\n";
    } else {
        cout << "Haitang\n";
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

2024牛客多校3BCrash Test

给定一个序列，在给定一栋墙，碰到墙会反弹，然后每个数可以无限次用，再给定一个起点，问我们离墙最近的距离。我们可以求出这个序列的所有的最大公约数，它可以构成他们任意的距离，通过枚举测试样例，我们可以发现，生成的距离有很多，我们都可以用这个最大公约数构成。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;
int main(){
    ll n, d;
    cin >> n >> d;
    ll res = 0;

    for(int i = 0; i < n; i ++){
        ll x;
        cin >> x;
        res = __gcd(res, x);
    }
    res = min(d % res, res - d % res);
    cout << res << endl;
    return 0;
}

AcWing 1291. 轻拍牛头

0 <= n <= 2 * 109 约数个数最多的数是100多个，

给定N个整数，求其他的数有多好个是他的约数， 1<=a <= 1e6;

将每个数累加到自己的倍数上去，我们直接离线处理就ok

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n);
    vector<int> m(1e6 + 10, 0);
    vector<int> s(1e6 + 10, 0);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        m[a[i]] ++;
    }
    int res = 0;
    for(int i = 1; i <= 1e6; i++){
        for(int j = i; j <= 1e6; j += i)
            s[j] += m[i];
    }
    for(int i = 0; i < n; i ++ )
        cout << s[a[i]] - 1<< endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    // int t;
    // cin >> t;
    // while (t--) {
        solve();
    // }
    return 0;
}

AcWing 1294. 樱花

求满足有多少个(1/x + 1/y) = 1/n!

如果固定一个变量，那么另一个也是固定的

我们推出有多少个x满足y，正整数当中满足条件的

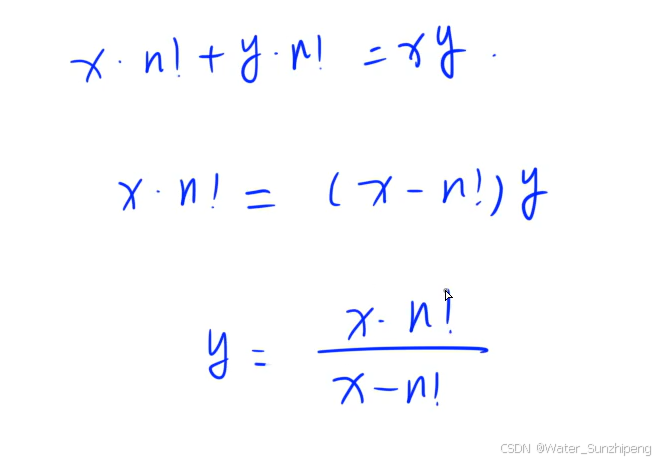
构造简化等式求n!^2的个数，x > n!, x的个数 == 满足 x - n!的个数 == 满足n!^2的约数个数。

所以我们要求n!^2的个数。可以进行阶乘分解。

n! = p1^c1 * p2^c2 ...pk^ck

稍微包装一下。分析起来有一定难度

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10, mod = 1e9 + 7;

typedef long long LL;
int primes[N], cnt;
bool st[N];

void init(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


void solve() {
    int n;
    cin >> n;

    init(n);
    int res = 1;
    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        int s = 0;
        for (int j = n; j; j /= p) s += j / p;
        res = (LL)res * (2 * s + 1) % mod;
    }

    cout << res << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    // int t;
    // cin >> t;
    // while (t--) {
        solve();
    // }
    return 0;
}

AcWing 198. 反素数

当一个题没有思路的时候可以想一下有没有什么性质。

1不同的质因子最多有9个

2每个质因子的次数最大是30 可暴搜

3.所有质因子一定是递减的

L1-006 连续因子

这题乍一看以为是数学题，实际上考察的是基础知识，由于范围很小，我们按照题意暴力枚举每一种情况 + 贪心，就可以求出这道题的答案

#include <bits/stdc++.h>
using namespace std;

void solve() {
    long long n;
    cin >> n;
    int maxLen = 0, start = 0;

    // 尝试找到最长的连续整数序列
    for (int i = 2; i <= n / i; i++) {
        long long temp = n;  // 用 long long 避免溢出
        int j = i;
        while(temp % j == 0){
            temp /= j;
            j ++;
        }
        if(j - i > maxLen){
            maxLen = j - i;
            start = i;
        }
    }
    // if(n == 1){
    //     cout << "0\n";
    //     return ;
    // }
    // 如果没有找到任何连续序列，输出 n 本身
    if (maxLen == 0) {
        cout << 1 << endl;
        cout << n << endl;
    } else {
        cout << maxLen << endl;
        for (int i = start; i < start + maxLen; i++) {
            if (i > start) cout << "*";
            cout << i;
        }
        cout << endl;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    solve();
    return 0;
}

快速幂指数操作

快速幂计算中，指数计算时不应对指数取模 MOD，而是应取模 MOD-1。不过考虑到 MOD 的特殊性，直接使用 MOD 也能得到正确结果。

欧拉定理告诉我们，对于任意一个整数 a 和一个整数 m，当 a 和 m 互质时，有：

aϕ(m)≡1 (mod m)

其中，ϕ(m)是欧拉函数，代表小于 m 且与 m 互质的整数个数。

具体到 m = MOD（998244353），MOD 是质数，因此 ϕ(MOD)=MOD−1这意味着：

a^{MOD-1} ≡1 (mod MOD) = a^b (mod (MOD−1))≡a^b (mod MOD)

转动齿轮

求2^{n*m} 对998244353取模

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const ll MOD = 998244353;

// 快速幂函数，计算 (base^exponent) % mod
ll quickPower(ll base, ll exponent) {
    ll res = 1;
    while (exponent > 0) {
        if (exponent & 1) {
            res = res * base % MOD;
        }
        base = base * base % MOD;
        exponent >>= 1;
    }
    return res;
}

int main() {
    ll n, m;
    cin >> n >> m;

    ll exponent = n % (MOD - 1) * (m % (MOD - 1)) % (MOD - 1);  // (n * m) % (MOD-1) to reduce the size of exponent
    ll total = quickPower(2, exponent);  // Calculate 2^(n*m) % MOD

    cout << total << endl;  // Output the result
    return 0;
}

公平组合游戏ICG

可以看成特殊的有向图游戏

NIM游戏

都采用相同的式子

假设有2 3 先手3 - 1，后手之后只需要按照前一个人做相同的操作，必赢。

必胜泰和必败态，相对于先手来说，拿完之后对面必败，那我就是必胜

那走ai -(ai - ai^x) = ai^ x

有向图游戏

SG函数

sg == 0必败， sg != 必胜，有很多个图，玩家可以操作任意一个图

看每一个图的起点亦或起来看必胜还是必败，把指数级别的状态变成一维状态

AcWing 893. 集合-Nim游戏

先手只能拿2个或者拿5个否则必败

我们可以求出初始状态sg的值可以求出sg(7)和sg(5)，求出每一堆sg的值，再进行亦或

#include <bits/stdc++.h>

using namespace std;

const int N = 110, M = 10010;

int n, m;
int s[N], f[M];


int sg(int x)
{
    if (f[x] != -1) return f[x];

    unordered_set<int> S;
    for (int i = 0; i < m; i ++ )
    {
        int sum = s[i];
        if (x >= sum) S.insert(sg(x - sum));
    }

    for (int i = 0; ; i ++ )
        if (!S.count(i))
            return f[x] = i;
}

void solve(){
    cin >> m;
    for (int i = 0; i < m; i ++ ) cin >> s[i];
    cin >> n;

    memset(f, -1, sizeof f);

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }

    if (res) puts("Yes");
    else puts("No");

    return ;
    
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

保持一致。1经典nim游戏。