二叉堆是一种高级数据结构,用于动态维护一个序列中的最值以及对某一个数的插入、删除。
我们现在首先定义一下二叉堆,二叉堆首先是一棵完全二叉树,而且根据对这里的最值定义,每一个节点都比其孩子节点更加靠近最值。举个例子,比如说我们要求最大值,那么每一个节点都比起孩子节点要大。这样的话,整一个序列的最大值就是第一个元素,我们称为Heap[1]。当然,我们也可以定义专门的常数root,使得Heap[root]是整个堆的根。下面如果没有特别声明,则root = 1。
既然二叉堆是一棵完全二叉树,那么我们就可以对于数组做出一些特殊的改变,使得二叉堆能够存到一个数组中去!虽然说树的结构存储完全可以用指针来实现,但是很显然,用指针比较容易错,而且用静态的内存池更加快,写起来也简单,所以在信息学竞赛中推荐使用数组的实现方式。如果我们要加入一个元素,那么由于其是一棵完全二叉树,插入的时候应该尽量向左放。如果我们将每一行从左向右标上号码,分别是root,root+1,root+2……n+root-1(在这里是1,2,3……n),那么就刚刚好能够存放在数组里,下标就是相应的号码了。而这样的话,直接在数组的最后放置元素也是符合原意的——这样能够尽量地向左放。我们来设想一下如果不放在这里呢?首先不可以放在这个位置前面,因为这样会扰乱顺序,破坏我们之前定义的性质“每一个节点都比其孩子节点要大”,如果放在后面的话,因为我们是从左往右标号,所以说放在后面的话要么和当前位置不在同一层,要么比其要更右。如果不在同一层,那么就浪费了空间(如果比当前位置高的话会扰乱,那么就只能够放低一些了),反之仍然违背了要求:尽量往左放。
接下来我们继续找一下规律。1有两个孩子,2和3,以此类推,那么我们可以很容易地得出一个规律:对于每个编号为p的节点,其的父亲的编号为
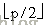 ,而其孩子的编号就分别为p*2和p*2+1(如果root=1的话)。乘2和除2都其实可以用位运算较为高效地实现,所以说比原来用指针的实现要更好!
,而其孩子的编号就分别为p*2和p*2+1(如果root=1的话)。乘2和除2都其实可以用位运算较为高效地实现,所以说比原来用指针的实现要更好!
那么,我们插入之后,就算插入的在尾部,也有可能打破性质。比如说我们现在要求最大值,接着我们现在插入了一个节点q,其下标为P(q),其父亲为F(q),其值为V(q),那么有可能V(F(q)) < V(q)。这是一种违背性质的情况,那么我们有什么方法呢?答案是交换q和F(q)。这样可以使得其重回稳定。另外,注意到假如q是F(q)的右孩子,那么F(q)的左孩子的V(left(F(q))必然不大于V(F(q)),所以说V(left(F(q))) < V(q),所以说我们交换了之后不必担心又要掉下来。但是可能仍然不满足,现在新的q可能又有V(F(q)) < V(q),那么就也只能对应地继续交换。这个交换的过程应该叫做Heapify-Up,我们可以看到q不断地在树中上升,所以是Up。
下面给出相应的代码实现:
const int MAXN = 10000000;
int n;
int Heap[MAXN];
void init(){
n = 0;
}
void Heapify_Up(int x){
while (x > 1){
if ((x >> 1) > 1 && Heap[x] > Heap[x >> 1]){
swap(Heap[x],Heap[x >> 1]);
x >>= 1;
}
else break;
}
}
void Insert(int num){
Heap[n] = num;
++n;
Heapify_up(n);
}
如果我们要删除某个数呢?
要删除某个数,比如说我们有一个数组,我们不注重其顺序,我们只需要不断地删除某些数。这俨然就是集合的初步定义,那么我们该怎样维护这个删除操作呢?二叉平衡树?No!我们只需要将最后一个在数组中的元素和要删除的这一个元素交换即可。如果是在尾端删除的话,肯定是O(1)的时间,而交换也相当于是O(1)的操作,所以说合起来就是O(1),比起二叉平衡树的O(log2n)要好。
那么,我们比如说要删除最大的元素(优先队列的支持操作),交换以后,很可能会又一次破坏性质,使得V(root)<V(left(root))或者V(root)<V(right(root))。那么,如果这两个中只有一个不满足性质的话,那就直接向下交换即可,交换向不满足性质的那一边。难题是,可能两个孩子都不满足性质!那么我们应该交换谁就成了一个问题。那么怎么解决呢?答案是,哪个孩子较大就交换哪一边。比如说我们令得V(root)<V(left(root))<V(right(root)),那么应该将root和right(root)交换。假如我们将root和left(root)交换,那么由于V(right(root))>V(left(root)),交换了之后不能够至少在root节点上满足这个性质,但是如果将其和right(root)交换,那么就可以仍然满足性质了。当然,有可能交换了之后仍然不满足,所以说仍然要继续维护下去。因为root是在树中一直往下的,所以说这个过程好像又叫Heapify-Down。
下面继续给出代码:
const int MAXN = 10000000;
int n;
int Heap[MAXN];
void init(){
n = 0;
}
void Heapify_Down(int x){
while (x < n){
if ((x << 1) < n && Heap[x << 1] > Heap[x]){
if ((x << 1) + 1 < n && Heap[(x << 1) + 1] > Heap[x]){
if (Heap[x << 1] > Heap[((x << 1) + 1)]){
swap(Heap[x],Heap[x << 1]);
x = x << 1;
}
else{
swap(Heap[x],Heap[(x << 1) + 1]);
x = (x << 1) + 1;
}
}
else{
swap(Heap[x],Heap[x << 1]);
x = x << 1;
}
}
else break;
}
}
void Delete_Root(){
swap(Heap[1],Heap[n-1]);
--n;
Heapify_Down(1);
}
接下来,我们可以继续考虑另一种堆的复杂操作,现在我们不止对最值的修改感兴趣了。我们要对每一个元素都能够修改!(删除其实也是同一个道理,也是交换,然后采用和修改差不多的维护操作)。
直接修改某一个元素,只要知道下标即可,并不是什么艰难的操作。关键就在于这个维护了。根据原来元素的性质,我们可以知道如果我们要将某个q改成q',那么有V(father(q)) > V(q),而如果我们假设V(left(q)) > V(right(q)),那么又有V(father(q)) > V(q) > V(left(q)) > V(right(q)),将q改成q'后,我们其实维护操作,都只是将这个不等式通过交换变得满足。首先,根据我们原来的不等式,我们有V(father(q)) > V(left(q)) > V(right(q)),那么我们只需要看一下V(q)到底在哪一边,接着不断地交换,以使其满足不等式即可。但是实际上在堆中修改元素似乎非常少用,而且比较难写,还是不写了(一共有6种情况,太麻烦了……)。
下面继续来说明一下其时间复杂度。
首先,由堆是完全二叉树可以知道最底一层的最左节点深度最大,而由节点q的左孩子下标是2*q可以知道,即使是从根节点(编号为1)出发,不断地往左孩子走,一直走到最左节点,最多有n个点,堆的完全二叉树的深度
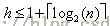
。
而由插入删除操作分别维护的当前节点一个是一直交换向上,一个一直交换向下可以知道,Insert和Delete_root操作的时间复杂度都是O(h)。由前面的
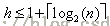 可知其时间复杂度都为O(log2n)。至此,我们得出结论:堆是一个非常高效的数据结构!
可知其时间复杂度都为O(log2n)。至此,我们得出结论:堆是一个非常高效的数据结构!
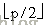 ,而其孩子的编号就分别为p*2和p*2+1(如果root=1的话)。乘2和除2都其实可以用位运算较为高效地实现,所以说比原来用指针的实现要更好!
,而其孩子的编号就分别为p*2和p*2+1(如果root=1的话)。乘2和除2都其实可以用位运算较为高效地实现,所以说比原来用指针的实现要更好!
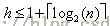 。
。
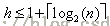 可知其时间复杂度都为O(log2n)。至此,我们得出结论:堆是一个非常高效的数据结构!
可知其时间复杂度都为O(log2n)。至此,我们得出结论:堆是一个非常高效的数据结构!






















 1831
1831

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








