☆【动态规划】【SCOI2011】地板

题目描述】
lxhgww的小名叫“小L”，这是因为他总是很喜欢L型的东西。小L家的客厅是一个的矩形，现在他想用L型的地板来铺满整个客厅，客厅里有些位置有柱子，不能铺地板。现在小L想知道，用L型的地板铺满整个客厅有多少种不同的方案？
需要注意的是，如下图所示，L型地板的两端长度可以任意变化，但不能长度为0。铺设完成后，客厅里面所有没有柱子的地方都必须铺上地板，但同一个地方不能被铺多次。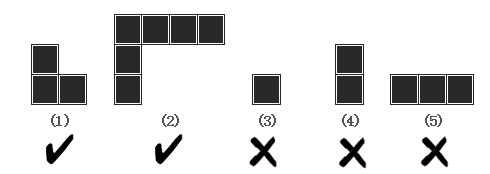

【输入】
输入的第一行包含两个整数，R和C，表示客厅的大小。
接着是R行，每行C个字符。’_’表示对应的位置是空的，必须铺地板；’*’表示对应的位置有柱子，不能铺地板。
【输出】
输出一行，包含一个整数，表示铺满整个客厅的方案数。由于这个数可能很大，只需输出它除以20110520的余数。
【样例输入1】
2 2
*_
__
【样例输出1】
1
【样例输入2】
3 3
___
_*_
___ 
【样例输出2】
8
【数据范围】
测试点编号                     数据范围
1, 2                            R*C <= 25
3, 4, 5                         R*C<=100并且(R = 2或者C = 2)
6, 7, 8, 9, 10                  R*C <= 100

这是一道基于连通性的状态压缩动态规划。

状态定义如下：设每个L型地砖都有两个不同伸展方向，并规定从转角处两端为向外，从两端到转角处为向内。使用0，1，3三种标记表示三种不同的插头，0表示没有插头，1表示向内的插头，3表示向外的插头。逐格递推，每次用一个四进制数来表示这一行所有插头的状态，按从左到右的顺序，左边为高位，右边为低位。

插图如下：

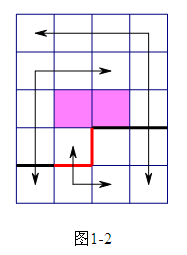
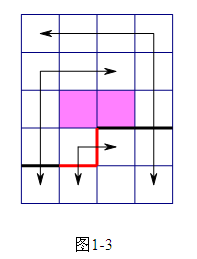
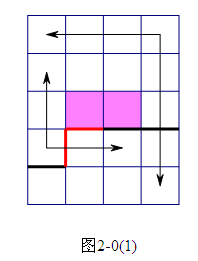
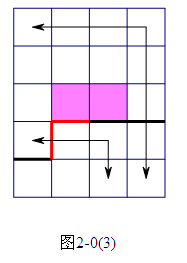
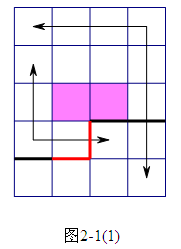
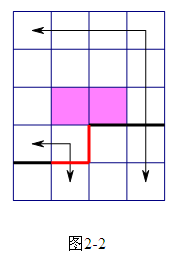
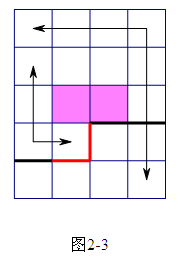
状态转移的时候，要用一个开散列记录状态，避免多次枚举。
Accode：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <bitset>

const char fi[] = "floor.in";
const char fo[] = "floor.out";
const int maxR = 110;
const int maxN = 1 << 18;
const int MOD = 20110520;
const int HMOD = 262143;

struct Node
{
    int S, ID;
    Node *next;
};

std::bitset <maxR> mp[maxR];
Node *Hash[HMOD + 1];
Node tmp[maxN];
int cnt[2];
int f[2][maxN];
int state[2][maxN];
//以上三个数组使用零壹滚动。
int n, m, pst, ths;

void init_file()
{
	freopen(fi, "r", stdin);
	freopen(fo, "w", stdout);
	return;
}

void readdata()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i < n + 1; ++i)
    {
        getchar();
        for (int j = 1; j < m + 1; ++j)
            if (getchar() == '_')
            {
                if (m > n) mp[j].set(i);
                else mp[i].set(j);
            }
    }
    if (m > n) std::swap(m, n);
	return;
}

inline void recover()
{
    cnt[ths] = 0;
    memset(Hash, 0, sizeof(Hash));
    return;
} //每次需要清空，为下次的状态转移做好空间。

inline int get_ID(int S)
{
    unsigned h = S & HMOD;
    for (Node *p = Hash[h]; p; p = p -> next)
        if (p -> S == S) return p -> ID;
	//若该状态已经被生成，则直接返回它的序号。
	//否则新建一个。
    tmp[++cnt[ths]].S = S;
    tmp[cnt[ths]].ID = cnt[ths];
    tmp[cnt[ths]].next = Hash[h];
    Hash[h] = &tmp[cnt[ths]];
    f[ths][cnt[ths]] = 0;
    state[ths][cnt[ths]] = S;
    return cnt[ths];
}

inline void Add(int &a, int b)
{
    a += b;
    if (a >= MOD) a -= MOD;
    return;
}

void work()
{
    pst = 0, ths = 1;
	//零壹滚动中的两指针。
    recover();
    f[ths][get_ID(0)] = 1;
	//置初始值为1。
    for (int i = 1; i < n + 1; ++i)
        for (int j = 1; j < m + 1; ++j)
        {
            std::swap(pst, ths);
            recover();
		//每次要记得清空。
            int q = (m - j) << 1;
		//记录当前需要转移的右插头的位置（相对于最右端）。
            int p = q + 2;
		//记录当前需要转移的下插头的位置（相对于最右端）。
            for (int k = 1; k < cnt[pst] + 1; ++k)
            {
                int val = f[pst][k];
		//当前状态的方案数。
                int Last = state[pst][k];
		//当前状态对应的四进制数。
                if (j == 1)
                {
                    if (Last & 3) continue;
                    else Last >>= 2;
                }
		//若换行，首先判断末尾是否有多余的插头，
		//若有，则此状态作废；否则将末尾的插头
		//移动到下一行的开头，以便下一行的转移。
                int wp = (Last >> p) & 3;
		//当前的右插头。
                int wq = (Last >> q) & 3;
		//当前的下插头。
                int Now = Last - (wp << p) - (wq << q);
		//构造一个新的插头，将转移的目标状态
		//所对应的两个插头先清空。
                if (!mp[i][j])
                {
                    if (!wp && !wq)
                        Add(f[ths][get_ID(Now)], val);
		//若该方块为障碍且无插头则可行。
                }
                else
                {
                    if (!wp && !wq)
		//无插头的情况，见图1-0。
		//此时可以新建插头，分三种情况讨论。
                    {
                        Add(f[ths][get_ID(Now | (1 << p))], val); //见图1-2。
                        Add(f[ths][get_ID(Now | (1 << q))], val); //见图1-1。
                        Add(f[ths][get_ID(Now | (3 << p)
                                          | (3 << q))], val); //见图1-3。
                    }
                    else if (!wp || !wq)
			//只有一个插头的情况。见图2-0(1)，2-0(2)，
			//2-0(3)以及2-0(4)，也要分情况讨论。
                    {
                        Add(f[ths][get_ID(Now | (wp << q)
                                          | (wq << p))], val);
			//延续原来的插头，见图2-1(1)和2-1(2)。
                        if (wp == 1) //见图2-0(2)。
                            Add(f[ths][get_ID(Last |
                                              (2 << p))], val);
			//插头可在此转弯，见图2-2。
                        else if (wq == 1)
                            Add(f[ths][get_ID(Last |
                                              (2 << q))], val);
			//同理如上。
                        else if (wp == 3 || wq == 3) //如图2-0(4)。
                            Add(f[ths][get_ID(Now)], val);
			//插头可在次终止，见图2-3。
                    }
                    else if (wp == 1 && wq == 1)
			//两插头相遇，可以构成一个L，见图3-0。
                        Add(f[ths][get_ID(Now)], val); //见图3-1。
                }
            }
        }
    printf("%d\n", f[ths][get_ID(0)]);
	return;
}

int main()
{
	init_file();
	readdata();
	work();
	return 0;
}

第二次做：

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <string>

const char fi[] = "floor.in";
const char fo[] = "floor.out";
const int maxN = 110;
const int maxSTATUS = 0x100000;
const int HMOD = 0x3ffff;
const int MOD = 20110520;

struct Node {int S, ID; Node *next;};
Node tmp[maxSTATUS], *Hash[HMOD + 1];
char mp[maxN][maxN];
int f[2][maxSTATUS], status[2][maxSTATUS];
int cnt[2], n, m, pst, ths = 1;

void init_file()
{
    freopen(fi, "r", stdin);
    freopen(fo, "w", stdout);
    return;
}

void readdata()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i)
    {
        scanf("\n");
        for (int j = 0; j < m; ++j)
        {
            char ch = getchar();
            if (m > n) mp[j][i] = ch;
            else mp[i][j] = ch;
        }
    }
    if (m > n) std::swap(n, m);
    return;
}

inline int get_ID(int S)
{
    int h = S & HMOD;
    for (Node *p = Hash[h]; p; p = p -> next)
        if (p -> S == S) return p -> ID;
    int ID = cnt[ths];
    tmp[ID].ID = ID;
    tmp[ID].S = S;
    tmp[ID].next = Hash[h];
    Hash[h] = &tmp[ID];
    f[ths][ID] = 0;
    status[ths][ID] = S;
    return cnt[ths]++;
}

inline void Add(int &a, int b)
{a += b; if (a >= MOD) a -= MOD; return;}

void work()
{
    f[ths][get_ID(0)] = 1;
    for (int i = 0; i < n; ++i)
    for (int j = 0; j < m; ++j)
    {
        std::swap(pst, ths); cnt[ths] = 0;
        memset(Hash, 0, sizeof Hash);
        int p = (m - j) << 1, q = p - 2;
        for (int k = 0; k < cnt[pst]; ++k)
        {
            int val = f[pst][k];
            int Last = status[pst][k];
            if (!j)
            {
                if (Last & 3) continue;
                else Last >>= 2;
            }
            int wp = (Last >> p) & 3,
            wq = (Last >> q) & 3,
            Now = Last - (wp << p) - (wq << q);
            if (mp[i][j] == '*')
            {if (!wp && !wq) Add(f[ths][get_ID(Now)], val);}
            else if (!wp && !wq)
            {
                Add(f[ths][get_ID(Now | (1 << p))], val);
                Add(f[ths][get_ID(Now | (1 << q))], val);
                Add(f[ths][get_ID(Now | (3 << p)
                           | (3 << q))], val);
            }
            else if (!wp || !wq)
            {
                Add(f[ths][get_ID(Now | (wp << q)
                           | (wq << p))], val);
                if (wp == 1) Add(f[ths][get_ID(Last |
                                 (2 << p))], val);
                else if (wq == 1)
                    Add(f[ths][get_ID(Last | (2 << q))], val);
                else Add(f[ths][get_ID(Now)], val);
            }
            else if (wp == 1 && wq == 1)
                Add(f[ths][get_ID(Now)], val);
        }
    }
    printf("%d\n", f[ths][get_ID(0)]);
    return;
}

int main()
{
    init_file();
    readdata();
    work();
    return 0;
}