数制转换（基于长除法的实现）

从二进制的转换出发

在之前的学习中我们已经掌握了十进制转化为二进制的方法，那便是“除2求余，逆序排列”的方法

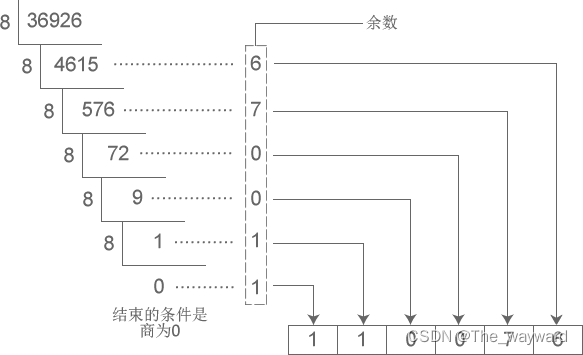
 实际上，对于其他数制的转化同样也可以采取类似的方法，只需重复求余后逆序排列的过程

实际处理中的问题

在我们进行编程时自然而然的想要使用这种方法来处理数制的转换，但是我们面对一些非常大的数字时似乎这个方法有点行不通了，就像114514114514114514这样的数据，其数位过长了之后已经无法直接使用long long等数据类型来进行储存与运算，只能通过数组来储存数据，为了解决这个问题，我们可以使用长除法。

长除法 

让我们以一个最基础的除法为例

 我们可以看到，在实际进行运算时，我们是对各位上的数字处理的。

以第一步为例子：4除以12商0余4，那么这个余数4就留给下一位，即4乘10加5，然后我们对45进行处理，45除以12商3余9，接下来9留下得到96，96除以12商8余0，此时所有数位我们都已处理完毕，这时的余数0就是456除以12的余数。

通过这样的观察，由于是对各位上的数字进行处理的特点，其可以很好的与数组结合。

//使用mod来表示上一位留下的余数，a[i]为数位上的数字,base为除数
a[i]=a[i]+mod*10;
mod=a[i]%base;

通过这样的结构，我们就实现了对各位数字的处理。

数制转换 

既然我们实现了大整数的除法，那么以除法为核心的模n求余自然就不是问题，只需要利用长除法进行迭代得到最后的结果。

#include <stdio.h>
#include <string.h>
  
int BASE; //数制的基
int DLEN; //待转数的长度
/*
进制转换递归函数：返回值，转换后的长度
【参数说明】
code: 存放转换结果的数组
a: 存放待转数的数组，a[0] 为最高位
k: 转换过程中，余数在code中的位置，从0开始
*/
//
int transform(int code[], int a[], int k)
{     
   int i; //在两个循环中使用
   for (i = 0; i < DLEN; i++)
   {//找到第1个非0数位  
       if (a[i] != 0)
       {
          break;
       }
   }
    
   if(i==DLEN) return k; //求余结束
   / 
    
   int _mod = 0;//余数初值, 即算第i位商时，第i-1位的余数。

    while(i<DLEN)
    {
        a[i]=a[i]+_mod*10;
        _mod=a[i]%BASE;
        a[i]=a[i]/BASE;
        i++;
    }

   code[k] = _mod; //得到一位
      
   return transform(code, a, k + 1); //继续求余
}
  
int main()
{
   char str[321] = {0};
   int nCode[1101] = {0}, nStr[321] = {0};
 
   gets(str);
   DLEN = strlen(str);
 
   scanf("%d", &BASE);
   for (int i = 0; i < DLEN; i++)
   {
       nStr[i] = str[i] - '0';
   }
 
   int codeLen = transform(nCode, nStr, 0);
   for (int i = codeLen - 1; i >= 0; i--)
   {
       printf("%d", nCode[i]);
   }

   return 0;
}

拓展：长除法的应用

除此以外，长除法显然可以应用于高精度运算，大整数除法等。