HNU信息安全数学基础实验四

一、实验内容

若p是奇素数，编程实现：

1）计算整数a模p的指数；

2）计算模p的所有原根g；

3）设置一个较大的p（十进制8-20位），分析并优化算法性能；对算法优化过程及计算结果进行讨论和分析；

要求：分步输出，有中间结果，最好窗口化。

二、实验目标

1. 掌握整数模运算的基本原理，熟悉如何计算一个整数在模p下的阶。

2. 巩固并实现计算模p下所有原根的方法，加深对原根性质的理解。

3. 通过设置较大的素数 p，分析算法的性能瓶颈并尝试优化，提升对大数运算中算法复杂度的认识。

4. 提升编程能力，尤其是在实现数学运算算法和性能优化方面的能力。

三、实验原理

5.1节定义1：

5.1节推论1：

5.2节定理1：

5.2节定理2：

四、实验设计

1）计算整数a模p的指数

首先，我们来计算整数a模p的整数。由推论1我们可以知道，对于a对模m的指数ordm(a)，只需要在p的欧拉函数值φ(p)的因数中寻找即可。因此，我们先通过euler_totient(p)函数求得p的欧拉函数值，并作为中间结果输出。然后，我们使用get_factors(phi_p)函数求得φ(p)的因数，也作为中间结果输出。

最后，我们从小到大遍历φ(p)的所有因数，使用mod_exp函数计算afactor模p的结果是否为1，如果为1则说明它是我们要求的指数，直接返回即可。

// 利用因数找出模 p 下的指数（阶）
long long mod_order(long long a, long long p){
    long long phi_p=euler_totient(p);
    cout<<"p 的欧拉函数值为："<<phi_p<<endl;
    vector<long long> factors=get_factors(phi_p);
    cout<<"φ(p) 的因数为：";
    for(int i=0; i<factors.size(); i++){
        cout<<factors[i]<<" ";
    }
    cout<<endl;
    for(long long factor:factors){
        if(mod_exp(a, factor, p)==1){
            return factor;
        }
    }
    return -1; // 如果找不到则返回 -1
}

接下来，我们来看一下求欧拉函数值的函数euler_totient()的具体实现。事实上，在实验一中我们已经详细解释过这个函数。

它首先定义result变量并赋初值p。然后从2开始遍历质因数i，逐步检测p是否可以被i整除。如果i是p的质因数，先将p中i的所有幂次去掉，再使用公式result=result×(1−1/i)=result−result/i逐步更新欧拉函数值。由于乘法是对称的，如12=2×6=6×2，因此在遍历因子的时候，我们不需要从i=2一直遍历到p，只需要遍历到sqrt(p)即可。

遍历结束后，意味着我们已经处理完所有小于等于sqrt(p)的质因数，这时可能会出现以下两种情况：

1.   p经过所有质因数的处理后，已经变成了1。这说明p原来的所有质因数已经被完全分解。

2.   p还剩下一个大于sqrt(p)的质数，这是因为在分解过程中，没有质数能够整除它。这种情况下，说明p自身是一个质数。

例如，对于p=13，所有小于等于sqrt(p)的质数（2和3）都不能整除13，因此经过循环之后，p仍然是13这个质数。

对于第二种情况，如果p在完成循环后仍然是一个大于sqrt(p)的质数，则需要将其本身这个质因数考虑进去。

在代码中，体现为在循环结束后，检查p是否大于1，如果p还大于1，说明p这个数本身是一个质数，并且在循环中没有被分解，要再用公式result=result×(1−1/p)=result−result/p更新欧拉函数值。如果p不大于1，说明p其已经在循环中被分解完毕了，则不用对结果result做进一步处理。

最终，result即为p的欧拉函数的最终值。

// 计算欧拉函数 φ(p)
long long euler_totient(long long p){
    long long result=p;
    for(long long i=2; i*i<=p; i++){
        if(p%i==0){
            while(p%i==0)
                p/=i;
            result-=result/i;
        }
    }
    if(p>1)
        result-=result/p;
    return result;
}

不过实际上，由于p是素数，我们不需要用这个函数计算它的欧拉函数值，因为它的欧拉函数值就是p-1。

然后，我们再来看看用来求φ(p)因数的函数get_factors()的具体实现。创建一个向量factors存储因数后，从1开始遍历到sqrt(n)，寻找n的因数i，并把i加入到factors向量中。同时，如果i不等于n/i，就把n/i也加入factors向量。最后对因数从小到大排序后，返回即可。

// 获取欧拉函数值的所有因数
vector<long long> get_factors(long long n){
    vector<long long> factors;
    for(long long i=1; i*i<=n; i++){
        if(n%i==0){
            factors.push_back(i);
            if(i!=n/i) // 防止重复因数
                factors.push_back(n/i);
        }
    }
    sort(factors.begin(), factors.end()); // 从小到大排序
    return factors;
}

2）计算模p的所有原根g

现在，我们来看看第二小问，计算模p的所有原根g。由定理5.2.2及课上习题例子我们可以知道，要求模p的所有原根，需要先找到模p的一个原根。找一个原根时，我们要先算出p-1的所有不同素因数q1，…，qs，然后对于g=2、3、4…逐个检查gp-1/qi是否是模p不同余1的。找到满足gp-1/qi模p不同余1(i=1,…,s)的第一个g就是我们找到的模p的一个原根。

在代码中，我们使用prime_factors()函数求出p-1的质因数保存在向量factors中，并作为中间结果输出。然后从2开始遍历g，直到使用is_primitive_root(g, p, factors)函数检查得到满足条件的一个原根g，也作为中间结果输出。

然后，根据这个原根生成所有原根。我们知道，当d遍历p-1的简化剩余系时，gd遍历p的所有原根。因此，我们遍历找到[1，p-1)中所有与p-1互素的d，然后使用函数mod_exp(root, d, p)求出所有的gd(mod p)，这就是我们所需要的所有原根，把它们加入到向量all_roots里，最后返回即可。

// 找到一个原根并生成所有原根
vector<long long> find_primitive_roots(long long p){
    long long phi_p=p-1;

    // 计算 p-1 的质因数
    vector<long long> factors=prime_factors(phi_p);
    cout<<"p-1 的质因数为：";
    for(int i=0; i<factors.size(); i++){
        cout<<factors[i]<<" ";
    }
    cout<<endl;

    // 找到一个原根
    long long root=-1;
    for(long long g=2; g<p; g++){
        if (is_primitive_root(g, p, factors)){
            root=g;
            break;
        }
    }
    cout<<"找到一个原根为："<<root<<endl;

    // 利用简化剩余系生成所有原根
    vector<long long> all_roots;
    for(long long d=1; d<phi_p; d++){
        if (__gcd(d, phi_p)==1) {
            all_roots.push_back(mod_exp(root, d, p));
        }
    }

    return all_roots;
}

接下来，我们来具体看一下求原根过程中用到的几个小函数。

首先是求p-1的质因数的函数prime_factors()，实际上，它和求欧拉函数值的函数过程非常类似，因此不再赘述。

// 分解 p-1 的质因数
vector<long long> prime_factors(long long n){
    vector<long long> factors;
    for(long long i=2; i*i<=n; i++){
        if(n%i==0){
            factors.push_back(i);
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1) factors.push_back(n);
    return factors;
}

然后是判断g是不是p的一个原根的函数is_primitive_root(g, p, factors)。对于prime_factors中的p-1的质因数，函数使用mod_exp(g, phi_p/factor, p)计算gp-1/factor(mod p)的结果是否为1，如果存在一个质因数使得这个结果为1，那么g就不是原根，返回false；而如果通过了循环，就说明对于所有的质因数，gp-1/factor(mod p)均不同余1，说明此时的g就是p的一个原根，返回true。

// 判断 g 是否为模 p 的原根
bool is_primitive_root(long long g, long long p, const vector<long long>& prime_factors){
    long long phi_p=p-1;
    for(long long factor:prime_factors){
        if(mod_exp(g, phi_p/factor, p)==1)
            return false; // 如果存在一个因数使得 g^(phi_p/factor) ≡ 1，则 g 不是原根
    }
    return true;
}

最后是计算bexp mod m的函数mod_exp(b, exp, m)，它其实就是我们在实验二中实现的模重复平方法。总的来说，就是通过指数的二进制表示来逐位处理每一位。对于每个二次项的系数，如果系数ni为1，则将当前的幂次值bi乘以上一轮结果ai-1得到新结果ai；如果系数ni不为1，则当前结果ai等于上一轮结果ai-1。每处理一位后，幂次值将被平方并取模，以适应下一位的处理。

// 模重复平方法计算 b^exp mod m
long long mod_exp(long long b, long long exp, long long m){
    long long a=1;
    b=b%m;
    while(exp>0){
        if(exp%2==1)
            a=(a*b)%m;
        exp/=2;
        b=(b*b)%m;
    }
    return a;
}

为了对算法的性能进行分析，代码中还增加了处理计算耗时的函数。使用chrono::high_resolution_clock::now()函数获取当前的时间点，用于记录起始和结束时间。然后用chrono::duration<double>这个类模板表示两个时间点之间的时间差（即持续时间），通过减去两个时间点得到的结果赋值给chrono::duration对象，然后调用.count()方法获得以秒为单位的耗时。

为了体现窗口化效果，代码还实现了选择任务功能。输入1时，代码执行任务1：计算整数a模p的指数；输入2时，代码执行任务2：计算模p的所有原根；输入3时，退出程序。此外，代码中还加入了控制台分隔线，以更明显的区分各部分输入输出。

此时，总代码如下：

#include <iostream>
#include <vector>
#include <cmath>
#include <chrono>
#include <algorithm>
using namespace std;

void print_separator(const string& section_name){
    cout<<"\n=========="<<section_name<<"==========\n"<<endl;
}

// 模重复平方法计算 b^exp mod m
long long mod_exp(long long b, long long exp, long long m){
    long long a=1;
    b=b%m;
    while(exp>0){
        if(exp%2==1)
            a=(a*b)%m;
        exp/=2;
        b=(b*b)%m;
    }
    return a;
}

// 获取欧拉函数值的所有因数
vector<long long> get_factors(long long n){
    vector<long long> factors;
    for(long long i=1; i*i<=n; i++){
        if(n%i==0){
            factors.push_back(i);
            if(i!=n/i) // 防止重复因数
                factors.push_back(n/i);
        }
    }
    sort(factors.begin(), factors.end()); // 从小到大排序
    return factors;
}

// 计算欧拉函数 φ(p)
long long euler_totient(long long p){
    long long result=p;
    for(long long i=2; i*i<=p; i++){
        if(p%i==0){
            while(p%i==0)
                p/=i;
            result-=result/i;
        }
    }
    if(p>1)
        result-=result/p;
    return result;
}

// 利用因数找出模 p 下的指数（阶）
long long mod_order(long long a, long long p){
    long long phi_p=euler_totient(p);
    cout<<"p 的欧拉函数值为："<<phi_p<<endl;
    vector<long long> factors=get_factors(phi_p);
    cout<<"φ(p) 的因数为：";
    for(int i=0; i<factors.size(); i++){
        cout<<factors[i]<<" ";
    }
    cout<<endl;
    for(long long factor:factors){
        if(mod_exp(a, factor, p)==1){
            return factor;
        }
    }
    return -1; // 如果找不到则返回 -1
}

// 判断 g 是否为模 p 的原根
bool is_primitive_root(long long g, long long p, const vector<long long>& prime_factors){
    long long phi_p=p-1;
    for(long long factor:prime_factors){
        if(mod_exp(g, phi_p/factor, p)==1)
            return false; // 如果存在一个因数使得 g^(phi_p/factor) ≡ 1，则 g 不是原根
    }
    return true;
}

// 分解 p-1 的质因数
vector<long long> prime_factors(long long n){
    vector<long long> factors;
    for(long long i=2; i*i<=n; i++){
        if(n%i==0){
            factors.push_back(i);
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1) factors.push_back(n);
    return factors;
}

// 找到一个原根并生成所有原根
vector<long long> find_primitive_roots(long long p){
    long long phi_p=p-1;

    // 计算 p-1 的质因数
    vector<long long> factors=prime_factors(phi_p);
    cout<<"p-1 的质因数为：";
    for(int i=0; i<factors.size(); i++){
        cout<<factors[i]<<" ";
    }
    cout<<endl;

    // 找到一个原根
    long long root=-1;
    for(long long g=2; g<p; g++){
        if (is_primitive_root(g, p, factors)){
            root=g;
            break;
        }
    }
    cout<<"找到一个原根为："<<root<<endl;

    // 利用简化剩余系生成所有原根
    vector<long long> all_roots;
    for(long long d=1; d<phi_p; d++){
        if (__gcd(d, phi_p)==1) {
            all_roots.push_back(mod_exp(root, d, p));
        }
    }

    return all_roots;
}

int main() {
    long long a, p;
    int choice;
    print_separator("输入部分");
    cout<<"请输入一个奇素数 p：";
    cin>>p;

    do{
        // 提示用户选择操作
        cout<<"\n请选择操作：\n";
        cout<<"1. 计算整数 a 模 p 的指数\n";
        cout<<"2. 计算模 p 的所有原根\n";
        cout<<"3. 退出程序\n";
        cout<<"输入您的选择：";
        cin>>choice;

        if(choice==1){
            // 计算整数 a 模 p 的指数
            print_separator("计算 a 模 p 的指数");
            cout<<"请输入一个整数 a：";
            cin>>a;
            auto start_order=chrono::high_resolution_clock::now();
            long long order=mod_order(a, p);
            auto end_order=chrono::high_resolution_clock::now();

            if(order!=-1){
                cout<<"模 "<<p<<" 下 a 的指数（阶） ord_"<<p<<"("<<a<<") = "<<order<<endl;
            }
            else{
                cout<<"未找到模 "<<p<<" 下 a 的阶。"<<endl;
            }

            chrono::duration<double> duration_order=end_order-start_order;
            cout<<"阶的计算耗时："<<duration_order.count()<<" 秒"<<endl;

        }
        else if(choice==2){
            // 计算模 p 的所有原根
            print_separator("计算模 p 的所有原根");
            auto start_roots=chrono::high_resolution_clock::now();
            vector<long long> roots=find_primitive_roots(p);
            auto end_roots=chrono::high_resolution_clock::now();

            cout<<"模 "<<p<<" 的所有原根为："<<endl;
            for(long long root:roots){
                //cout<<root<<" ";
            }
            cout<<endl;

            chrono::duration<double> duration_roots=end_roots-start_roots;
            cout<<"原根计算耗时："<<duration_roots.count()<<" 秒"<< endl;
        }
        else if(choice==3){
            cout<<"程序已退出。"<<endl;
        }
        else{
            // 处理无效输入
            cout<<"无效输入，请重新选择。"<<endl;
        }

    } while(choice!=3);

    return 0;
}

现在，我们用课堂上的例子来验证一下这个程序。

可以看到，我们计算2模43的指数，结果正确。

计算模43的所有原根，结果正确。并且当输入3时，成功退出。

3）设置一个较大的p（十进制8-20位），分析并优化算法性能；对算法优化过程及计算结果进行讨论和分析

（一）初步分析

首先，我们对目前的代码进行一下算法性能及复杂度分析。

1. 模幂运算mod_exp

mod_exp函数使用模重复平方法来计算b的exp次幂模m，其时间复杂度为 O(log(exp))。这是因为该算法每次将指数exp减半，直到exp为零。

2. 获取欧拉函数的所有因数get_factors

get_factors函数用于获取欧拉函数值phi(p)即p-1的所有因数，其中p是一个大素数。函数通过检查从 1 到 sqrt(p-1) 的每个整数来找到因数对，因此复杂度为 O(sqrt(p-1))。

3. 计算整数a模p的指数mod_order

mod_order函数通过逐个检查phi(p)的每个因数，调用mod_exp(a, factor, p)来验证其是否为指数。其时间复杂度取决于get_factors的输出大小和mod_exp的复杂度，大约为O(k * log(phi(p)))，其中k是phi(p)的因数个数。

4. 判断是否为原根is_primitive_root

is_primitive_root函数用于检查一个数g是否是模p的原根。它遍历p-1的每个质因数，并调用mod_exp来验证条件g(p-1)/factor模 p不等于 1。其复杂度大约为O(m * log(p))，其中m是p-1的质因数个数。

5. 找到所有原根find_primitive_roots

find_primitive_roots首先找到一个原根，然后通过遍历p-1的简化剩余系的整数d来生成所有原根。生成的每个原根需要调用mod_exp来计算原根root的d次幂模p。其复杂度大约为 O(phi(p) * log(p))。

整体性能分析

• 时间复杂度：

计算整数a模p的指数的复杂度约为O(k * log(p))，其中k是phi(p)即p-1的因数个数

寻找和生成所有原根的复杂度约为O(phi(p) * log(p))，其中phi(p)即p-1。

因此，当p较大时，计算所有原根的操作会变得相对耗时，特别是在大素数情况下。

• 空间复杂度：

主要由存储因数和原根的vector构成，因此空间复杂度是O(phi(p))。

如果p较大，存储所有原根可能会耗费较多内存。

（二）初步测试

分析结束后，我们来具体用较大的质数p来运行一下程序，看看结果如何。

对于较大的p，可以在网上找到大质数表，部分内容如下：

因此，首先我们用目前的程序来试试8位素数10000019，9位素数100000007，10位素数1000000007。对于任务1，我们求2模p的指数。运行后结果如下。

可以看出，运行速度都非常快，计算耗时均接近0秒。因此，我们接下来的性能分析和算法优化主要聚焦于任务2，即求模p的所有原根的性能。

而对于任务2，计算模p的所有原根，将所有原根值都输出的话会非常多，一时半会难以得到耗时，因此我们暂时将用于输出原根的cout语句注释掉。

可以看到，计算模8位素数10000019的所有原根耗时为3秒左右。

计算模9位素数100000007的所有原根耗时为40多秒。

然而，在计算模1000000007这个10位素数的所有原根时，出现了terminate called after throwing an instance of 'std::bad_alloc' what():  std::bad_alloc的错误。

（三）优化一

查阅资料得知，std::bad_alloc是C++标准库中的一种异常，表示在尝试分配内存时失败。出现这个错误通常意味着程序试图分配的内存超过了可用内存的限制，或者系统无法满足内存分配的请求。

既然std::bad_alloc主要是因为内存不足导致的，而在目前的代码中，对于较大的素数p，生成所有原根并保存在all_roots向量里可能会占用大量内存。因此我首先尝试通过减少不必要的中间数据存储来优化内存使用。

修改find_primitive_roots()函数，在找到每个原根后直接输出，避免将它们全部存储在vector中，这样可以显著减少内存的占用。具体修改如下：

// 找到一个原根并生成所有原根
void find_primitive_roots(long long p){
    long long phi_p=p-1;

    // 计算 p-1 的质因数
    vector<long long> factors=prime_factors(phi_p);
    cout<<"p-1 的质因数为：";
    for(int i=0; i<factors.size(); i++){
        cout<<factors[i]<<" ";
    }
    cout<<endl;

    // 找到一个原根
    long long root=-1;
    for(long long g=2; g<p; g++){
        if (is_primitive_root(g, p, factors)){
            root=g;
            break;
        }
    }
    cout<<"找到一个原根为："<<root<<endl;

    // 利用简化剩余系生成并直接输出所有原根
    cout<<"模 "<<p<<" 的所有原根为："<<endl;
    for(long long d=1; d<phi_p; d++){
        if(__gcd(d, phi_p)==1){
            //cout<<mod_exp(root, d, p)<<" ";
        }
    }
    cout<<endl;
}

我们仍然暂时将用于输出原根的cout语句注释掉。

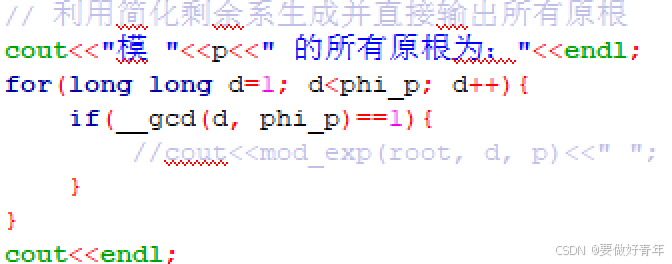
可以看到，计算模8位素数10000019的所有原根耗时为不到1秒。

计算模9位素数100000007的所有原根耗时为10秒左右。

此时计算模10位素数1000000007的所有原根成功，耗时为不到2分钟。

然而，当我用11位素数10000000019执行任务1，计算2模10000000019的指数时，输出为：未找到模10000000019下a的阶。显然这是一个错误的答案，因为按理说是一定存在的，最大为10000000019的欧拉函数值。

于是，我直接调用函数mod_exp(a, 10000000018, 10000000019)，得到的返回值居然是0而不是1。显然，函数mod_exp出现了问题。

（四）优化二

由于现在的数字很大，因此怀疑是存在整数溢出问题。即使我们已经使用了long long类型，但目前的mod_exp()函数中乘法都是直接相乘的，使得中间结果仍然可能超出long long 的存储范围，从而导致错误的计算结果。

既然在大数运算时，直接计算a*b可能会导致整数溢出，无法得到正确结果，那么我们可以手动模拟大数乘法，将乘法分解为逐步加法和取模的操作，从而避免溢出。

具体步骤如下：

①我们把b看作是一个二进制数，从最低位到最高位逐位处理（例如b=13的二进制是1101，从右往左逐位处理）。

②对于b的每一位，如果该位为1，则将当前的a加到结果中（这相当于把a乘上这一位对应的权重，并加到总和中）；如果为0，则结果不变。每次加法后都立即对m取模，确保中间结果不超出范围。

③在二进制中，每处理完一位后，将a乘2（即左移一位），以便在下一次迭代中准备加上正确的权重。同时，将b右移一位，准备处理b的下一位。

④当b的所有位处理完毕时，b为0，循环结束，得到最终结果。

简单示例如下：

假设a=3，b=13（二进制1101），m=7，我们想计算(3*13)%7：

初始化：result=0，a=3，b=13。

处理b的每一位：

最低位：b=1101（最低位为1），result=(0 + 3)%7=3，然后a=(3*2)%7=6，b 右移一位。

第二位：b=110（最低位为0），跳过加法，然后a=(6*2)%7=5，b右移一位。

第三位：b=11（最低位为1），result=(3+5)%7=1，然后a=(5*2)%7=3，b右移一位。

第四位：b=1（最低位为1），result=(1+3)%7=4，然后a=(3*2)%7=6，b右移一位。

最终结果：b=0时结束，得到result=4，所以(3*13)%7=4。

这种方法将乘法分解为逐步加法和取模，在每一步都保证结果不超出模数范围，避免了溢出问题，因此可以安全地用于大数运算。

根据这个方法，修改mod_exp()函数如下：

long long mul_mod(long long a, long long b, long long m){
    long long result=0;
    a=a%m;
    while(b>0){
        if(b%2==1){
            result=(result+a)%m;
        }
        a=(a*2)%m;
        b/=2;
    }
    return result;
}

// 模重复平方法计算 b^exp mod m
long long mod_exp(long long b, long long exp, long long m){
    long long a=1;
    b=b%m;
    while(exp>0){
        if(exp%2==1){
            a=mul_mod(a, b, m); // 等价于a=(a*b)mod m
        }
        exp/=2;
        b =mul_mod(b, b, m); // 等价于b=(b*b)mod m
    }
    return a;
}

优化完成后，我们再次运行程序执行任务1，计算2模10000000019的指数，此时输出正确，找到了2模10000000019的指数为10000000018。

同时，我们运行程序执行任务2，可以看到，计算模11位素数10000000019的所有原根，耗时为20分钟左右。

然后，更进一步，我们使用12位素数100000000003再执行任务1，计算2模100000000003的指数。如下所示，计算正确并且速度非常快。

对其执行任务2，计算模12位素数100000000003的所有原根，耗时为接近4个小时。

最最后，对于计算模13位素数1000000000039的所有原根这个任务，使用现有代码执行一天以后也没有完成，因此到此为止。

五、实验结果

实验中能算出所有原根的最大素数为12位，时间花费接近4个小时。对于13位素数，算法执行时间超过一天，因此并未继续执行下去了。

对于进一步优化的思考，可以考虑更换载有更好CPU的电脑，这样应该可以显著提升计算速度，尤其是在大数模运算和原根查找等整数密集型任务中。此外，更好的CPU还可以更流畅的进行多线程计算，利用更多核心和线程来并行执行运算任务，从而提高效率。