bundled camera paths for videos stabilization 论文翻译 卷帘快门（Rolling Shutter）讲解

作者

http://www.liushuaicheng.org/

MATLAB代码和视频

http://www.liushuaicheng.org/SIGGRAPH2013/index.htm

详细图解，一眼就能看懂！卷帘快门（Rolling Shutter）与全局快门（Global Shutter）的区别：

https://blog.csdn.net/abcwoabcwo/article/details/93099982

翻译：

多摄像机路径以实现视频稳定（bundled一捆）

 

图一：传统二维稳定（单个全局摄像机路径）与我们的捆绑摄像机路径稳定的比较。我们绘制相机轨迹（通过y轴随时间的平移可视化），并显示两种方法的原始路径（红色）和平滑路径（蓝色）。我们的多路径依赖于基于二维网格的运动表示，并在时空中进行平滑处理。

摘要

我们提出了一种新颖的视频稳定方法，该方法使用一捆（多条）摄像机路径束对相机运动进行建模。 所提出的模型基于网格的空间变化运动表示和自适应时空路径优化。 我们的运动表示使我们能够从根本上处理视差和卷帘效果，而无需长特征轨迹或稀疏的3D重建。 我们引入了“尽可能相似”的想法，以使运动估计更加可靠。 我们的时空路径平滑通过在统一的优化框架中考虑不连续性，裁剪大小和几何失真来自适应地调整平滑强度。对各种消费者视频的评估证明了我们方法的优点。

1. 简介

用手持设备（例如手机或便携式摄录机）拍摄的视频通常会出现明显的抖动和失真。 数字视频稳定可以通过消除不必要的摄像机运动来提高视频质量。 这具有非常重要的现实意义，因为能够捕获视频的设备（移动电话，平板电脑，便携式摄像机）已经普及，在线共享变得无处不在。

先前的视频稳定方法通过估计和平滑2D摄像机运动来合成新的稳定视频[Matsushita等。 2006年;Grundmann等。2011]或3D相机运动[Liu等。2009; 刘等。2012]。通常，二维方法更健壮，速度更快，因为它们仅估计连续帧之间的线性变换（仿射或单应性）。 但是2D线性运动模型太弱，无法从根本上处理由场景中非平凡的深度变化引起的视差。 相反，3D方法原则上可以处理视差并产生非常稳定的结果。但是，他们的运动模型估计对于各种退化（如特征跟踪失败，运动模糊，相机缩放和快速旋转）的鲁棒性较低。 简而言之，2D方法更健壮，但可能会牺牲质量（例如，引入令人不快的几何变形或产生较少的稳定输出），而3D方法可以实现高质量的结果，但更脆弱。

最近的一些方法[Liu等。2011; Goldstein和Fattal 2012]成功地结合了这两种方法的优点。 刘等[2011]在2D特征轨迹上应用了低秩子空间约束，这是3D重构的有效简化。Goldstein和Fattal [2012]通过利用“极极转移”技术避免了3D重建。 这些方法放宽了从3D重建到2D长特征跟踪的要求。然而，需要长时间的特征跟踪（通常超过20帧）使得难以在消费者视频中处理更具挑战性的情况（例如，快速运动，快速场景过渡，大遮挡）。

本文的目标是获得可靠的高质量结果，但目标却相反：我们提出了一个更强大的2D相机时代运动模型。 具体来说，我们提出了捆绑的相机路径模型，该模型可维护多个空间变化的相机路径。 换句话说，视频中的每个不同位置都有其自己的摄像头路径。 这种灵活的模型使我们能够从根本上处理由视差和卷帘效应引起的非线性运动[Liang等.2008;贝克等.2010; Grundmann等.2012]。同时，该模型具有2D方法的鲁棒性和简单性，因为它只需要两个连续帧之间的特征对应即可。

我们的多相机路径模型基于两个新颖的组件：一种基于弯曲的运动表示（和估计）以及自适应时空路径平滑算法。第一个组件通过具有基于网格的“尽可能相似”正则化约束的空间单应性变换（图1（b））来表示两个连续帧之间的运动[Igarashi等.2005; Schaefer等.2006]。此约束至关重要，因为在特征不足或遮挡较大的情况下，估计具有如此高自由度的模型通常是有风险的。据我们所知，这是第一次将基于网格的“尽可能相似”正则化用于视频稳定中的空间可变运动估计。请注意，[Liu et al.2009；Liu et al.2011]中使用了“尽可能相似”的翘曲来实现视频稳定。但是我们直接使用网格顶点作为运动模型本身。没有使用中间表示，例如三维重建[Liu等人.2009]或子空间[Liu等人.2011]

基于已经被提出的运动表示方法，我们构造了一组图像路径，每个图像路径都是随着时间的推移在同一网格单元上的局部单应性的级联（图1（b））。 我们的第二个组件将所有的相机路径作为一个整体进行平滑处理，以保持空间和时间的连贯性。 此外，为了避免过度的裁剪/几何失真和近似的图像首选路径，我们采用了类似于双边滤波的不连续性保存思想[Tomasi and Manduchi 1998]来自适应地控制平滑强度。

为了进行定量评估，我们提供了一个全面的数据集（包括公共示例和我们自己的各种运动视频片段）。 我们表明，我们的新2D方法可与其他竞争性2D或3D方法媲美或优于其他竞争性2D或3D方法。

2. 相关工作

2D方法

估计连续视频帧之间的2D转换，并随时间平滑它们以生成稳定的视频。以前开发的大多数方法都应用仿射或单应性模型，并着重于平滑算法的设计。早期作品[Morimoto and Chellappa 1998; 松下等. 2006]将低通滤波器应用于各个模型参数。一些方法假设先验运动模型，例如多项式曲线[Chen等2008]。Gleicher和Liu [2007]将原始相机轨迹分为多个段，以进行后续的个体平滑处理。 最近，[Grundmann等人.2011]优雅地应用L1范数优化来生成由恒定，线性和抛物线运动组成的摄影机路径，该运动遵循摄影规则。Grundmann等。[2012]进一步采用基于单应性阵列的运动模型来处理卷帘快门效果。这两种技术已集成到Google YouTube中。它功能强大，遵循摄影规则，并在许多消费者视频上表现良好。

我们的方法属于这一类。 但是我们使用空间变化模型来表示视频帧之间的运动，并为此模型设计适当的平滑技术。

3D方法

通常依靠鲁棒的特征跟踪来实现稳定。Beuhler等[2001]用未校准的摄像机对场景进行投影3D重建来实现稳定。 刘等.[2009]开发了第一个成功的3D视频稳定系统，并且是第一个引入“内容保留”变形以稳定的系统。

由于3D重建很困难，因此最近的方法直接平滑了跟踪特征的轨迹。刘等.[2011]平滑了特征轨迹形成的子空间的一些基本轨迹（最好长于50帧）。该方法达到了与基于3D重建的方法相似的质量，同时减少了从3D重建到长特征跟踪的需求。 它已被称为“ Warp Sta bilizer”的功能转移到Adobe After Effects。  Goldstein和Fattal [2012]利用“极极转移”技术来避免脆弱的3D重建。该技术还减轻了长特征轨迹上的应力。 但是它仍然需要适中的特征轨道长度（通常超过20帧）。 在光场摄像机视频稳定工作中也使用了特征轨迹平滑功能[Smith等.2009]。为了解决遮挡问题，Lee等人.[2009]引入特征修剪以选择鲁棒的特征轨迹进行平滑。

 

几乎所有涉及特征跟踪的方法都面临一个共同的障碍–在许多消费者视频中，由于遮挡，运动模糊或摄像机快速运动，获得较长的特征轨道非常脆弱。 我们的方法没有遇到这个问题，因为它只计算连续帧之间的相对运动。

 

运动估计

功能可计算视图重叠的两个图像之间的过渡。 光流算法[Lucas and Kanade 1981]通过每个像素处的单个位移矢量对这种过渡进行建模。当没有视差时，可以通过全球单应性转换很好地表示这种过渡[Hartley and Zisserman 2003]。 局部比对[Shum and Szeliski 2000]或双重单应性模型[Gao等.2011]可以减少视差引起的对准误差。Szeliski和Shum [1996]使用样条模型的混合来表示运动，该样条模型具有空间变异的空间支持以方便配准。Lin等.[2011]估计平滑变化的仿射场，以对齐大视点变化的图像。 此模型可以潜在地用于视频稳定。但是，其当前的运动估计技术很慢（可能需要8分钟才能处理720p帧）。

 

我们的运动模型本质上是基于网格的，空间变异的单应性模型，其灵感来自于最近的图像变形技术[Igarashi等2005;Schaefer等.2006年;刘等.2009]。我们将“尽可能相似”的想法从图像合成扩展到运动估计，并将其应用于视频稳定。 估计我们的运动模型非常有效（可能只需要50毫秒即可处理720p帧）。

 

卷帘快门去除

估计并校正由行平行读数引起的行间运动，即主要在CMOS传感器中使用的电子卷帘快门[Nakamura 2005]。现有技术设计了不同的参数行间运动模型，包括每行转换模型[Liang等.2008; 贝克等.2010]和3D旋转模型[Forssen and Ringaby 2010]。最近，Grundmann等人.[2012]提出了一种无标定单应混合物模型，显示出显着的改进。Karpenko等.[2011]使用专用硬件–移动设备上的陀螺仪来实时纠正卷帘效果。

 

与[Grundmann et al.2012]，我们的方法无需事先校准即可校正卷帘效果。我们基于翘曲的模型自然将滚动快门效果作为一种特殊的空间变化运动来处理。 因此，在稳定过程中，我们不需要单独的卷帘快门校正步骤。

 

3. 多相机路径

在本节中，我们介绍基于扭曲的运动模型和捆绑的相机路径。

3.1 基于变形的运动模型

我们建议使用图像变形模型来表示连续视频帧之间的运动，与传统的单二维线性变换相比，它提供了更强大的建模能力。虽然本文中我们采用了变形模型方法[Igarashi et al.2005；刘等.2009年]，但是其他一些方法，如[Schae-fer等人]论文中使用的 “移动最小二乘法”或者[Nir等人.2008年]提出的参数化光流方法都可以被使用。

 

图2：（a）用规则网格对两帧之间的运动进行参数化，其中一对匹配的特征（p，pˆ）应该用其四个封闭顶点的相同双线性插值来表示。（b）尽可能相似项要求每个三角形v，ˆvˆ0，vˆ1遵循相似变换。

 

模型

在每帧上，我们定义一个统一的网格，如图2所示。运动由网格的（未知）扭曲来表示，以注册两个帧（实际上，它们对应的特征点）。我们需要匹配的特征（如图2中的p和pˆ）来共享扭曲后封闭网格单元四个角点的相同双线性插值。在第i个网格单元处，从帧t到帧t +1的扭曲引入了单应性Fi（t），可以根据四个封闭顶点的运动来确定单应性。因此，基于扭曲的运动模型实际上是2D网格上的一组空间变异单应性。

请注意，这种高度灵活的模型能够处理视差。它介于整体单应性和按像素的光流之间。 但是，估计具有如此高的自由度的模型非常冒险，因为我们可能在每个单元中没有足够的特征（由于无纹理区域或遮挡）。

正则化

为了解决这一挑战，我们建议采用形状保持（即“尽可能相似”）的方法[Igarashi et al。2005]）约束。 形状保持和网格表示的组合在一起提供了两种正则化：

1. 对于每个单元，应将拟合的单应性偏向于减少的相似性（或刚性）变换；  
2. 网格的固有连接（两个相邻的网格单元共享两个顶点）强制执行一阶连续性约束。它们可以帮助从具有足够特征的区域向其他区域传播或填充信息。

最后，我们通过最小化两个能量项来估计运动：一个用于匹配特征的数据项，一个用于执行正则化的形状保留项。

 

3.2模型估计

我们首先按照[Liu et al.2009]，并在下一小节中对其进行了扩展以提高鲁棒性。

数据项

如图2所示，假设{p，pˆ}是从帧t到帧t + 1的第p个匹配特征对。特征p可以用四个顶点Vp = [v1p，v2p，v3p，v4p]封闭网格单元的：p = Vpwp，其中wp = [w1p，w2p，w3p，w4p]⊤是总和为1的插值权重。我们期望相应的特征pˆ可以用相同的权重表示为扭曲的网格顶点Vˆp = [ˆv1p，vˆ2p，vˆ3p，vˆ4p]。

因此，数据项定义为

 

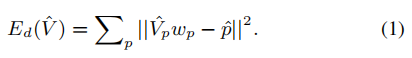
这里Vˆ包含所有扭曲的网格顶点。求解Vˆ决定了网格的翘曲。

 

保持形状项

我们使用类似[Liu et al.2009]论文中的保持形状方法包含Vˆ中的所有顶点，

 

其中s =∥v-v1∥/∥v0-v1∥是从初始网格计算出的已知标量。这个保形项要求相邻顶点v，v0，v1的三角形遵循相似变换。

线性组合两个项形成我们的最终能量E（Vˆ）:

 

其中，α是控制正则化量的重要权重。 稍后我们将讨论如何自适应地确定它。 由于能量E（Vˆ）是二次方的，所以可以通过稀疏线性系统求解器轻松地求解变形的网格Vˆ。

 

估计单应变换

有了新的网格后，我们可以通过求解线性方程：

来估计框架t的网格i中的每个局部单应性Fi（t），

 

其中Vi和Vˆi是四个 变形前后的顶点。

图3显示了根据估计运动的扭曲网格。左边和右边是带有和不带有形状保留项的结果。显然，正则化项有助于保持平滑的变化网格表示。

 

3.3稳健估计

我们进一步推广了运动估计，以使其更加可靠。

异常排除

我们拒绝两种比例的不正确匹配的功能。在粗略尺度上（整个图像），我们应用RANSAC算法[Fischler and Bolles 1981]来拟合全局单应性F（t），并通过相对较大的拟合误差阈值（图像宽度为6％）来丢弃特征。 在精细比例（4×4子图像）下，我们再次应用RANSAC来以相对较小的脱粒时间（图像宽度的2％）拒绝特征。

预变形

为了便于变形估计，我们使用全局单应性F（t）使匹配特征更接近。 然后，我们对翘曲进行求解，以估计残余运动，从而在每个网格单元处生成全息图F'i（t）。 最终单应性Fi（t）可以简单地计算为F'i（t）×F（t）。 注意[Liu et al.2009]用于图像合成，并在运动估计文献中证明有效[Brox等.2004]。

自适应正则化

一个好的正则化应该与图像内容相适应。例如，如果可靠的特征均匀分布在整个图像上，我们应该更信任数据项，并在等式3中使用较小的权值α来进行较弱的调节。但是当数据项存在遮挡或特征不足时，我们更倾向于使用更强的正则化方法，因为数据项的可靠性较差。为了实现这一策略，我们根据拟合误差eh和平滑度误差es自适应地设置每帧α。

 

拟合误差eh是在估计的单应性下特征匹配的平均残差，即eh = 1n∑p∥Fp×pp pˆ∥2，其中Fp是包含p的单元中的单应性。 特征对的数量。 平滑度误差es通过es = β∑j∈Ωi∥FiiFj∥2来度量相邻局部单应性之间的相似度（L2距离），其中Ωi由i的相邻像元组成。 在此，对单应性矩阵进行归一化，以便其所有元素之和为1。 我们凭经验设置β= 0.01，因为在大多数示例中，它使eh和es的比例相似。 然后，将组合误差定义为e = eh + es。

   我们将α离散化为0.3到3之间的10个值。我们使用每个离散化的值执行模型估计，并选择具有最小误差e的模型。

 

如图4（a）所示，对于具有平滑深度变化的简单场景，相邻单元往往具有相似的单应性。 因此，我们选择一个小的α（= 0.9）以更好地最小化数据误差。 相反，对于具有较大遮挡的场景（图4（b）），相邻的局部单应性不太相似。 通过增加α，可以大大降低平滑度误差。 因此，我们的系统将自动选择较大的α（= 3.0），以确保一致的局部运动。

 

最后，我们在图5中显示了一个示例，以验证我们方法正则化的强度。 在此示例中，我们比较使用所有特征和特征子集估算的两个网格。 两个类似的结果表明，我们的方法可以可靠地处理特征不足的区域。

 

3.4 多相机路径

利用估计的局部单应性，我们可以为整个视频定义一束空间变化的摄像机路径。 令Ci（t）为第t帧的网格像元i的摄影机姿态。 它可以写成：

Ci(t) = Ci(tt 1)Fi(tt 1), ⇒ Ci(t) = Fi(0)Fi(1)· · · Fi(tt 1),

 

其中{Fi（0），...，Fi（t t 1）}是在同一网格单元i上估计的局部单应性，如图6（a）所示。 我们将这些空间变化的路径称为“多相机路径”。 在下一节中，我们将介绍如何平滑这些捆绑的路径以实现视频稳定。

 

4 路径优化

 

我们首先描述针对单个摄像机路径的平滑方法，然后将其扩展到一系列摄像机路径。

 

4.1优化单个路径

良好的相机路径平滑度应考虑多个竞争因素：消除抖动，避免过度裁剪以及最小化各种几何变形（剪切/倾斜，摆动）。 为了达到理想的平衡，我们提出了一个考虑所有因素的基于优化的框架。

公式

给定原始路径C = {C（t）}，我们通过最小化以下函数来寻求优化路径P = {P（t）}：

其中Ωt是帧t处的邻域。 其他术语为：

•数据项∥P（t）⇒C（t）∥2强制新的相机路径接近原始路径，以减少裁剪和失真；

•平滑项∥P（t）⇒P（r）∥2稳定路径；

•权重ωt，r（C）以在快速平移/旋转或场景转换下保持运动不连续；

•参数λt平衡以上两项。

因为方程5是二次的，所以我们可以用任何线性系统来求解它。这里，我们使用基于雅可比的迭代解算器[Bronshtein and Semendyayev 1997]：

 

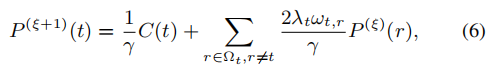
其中γ=1+2λt∑r∈Ωt，r=tωt，r，ξ是一个迭代指数。

初始化时，P（0）（t）=C（t）。一旦我们得到优化路径P，我们计算翘曲变换B（t）=c1（t）P（t），以将原始视频帧扭曲到稳定的结果（图6（B））。

保持不连续性

自适应权重ωt，r对于保持运动不连续性很重要。 我们遵循双边滤波器的思想[Tomasi and Manduchi 1998]，并通过两个高斯函数对其进行设计：

 

其中Gt（）为附近的帧赋予更大的权重。  Gm（）测量两个相机姿势的变化。

我们使用大内核来确保成功抑制高频抖动（例如握手）和低频跳动（例如步行）。 在我们的实现中，我们将Ωt设置为60个相邻帧，将Gt（）的标准偏差设置为10。相反，以前的基于低通滤波的方法[Matsushita等.2006年]通常需要较少量的支撑（例如10帧），以避免过度裁剪和变形。但是，这么小的内核通常不足以抑制低频反弹。

 

我们可以使用更大内核的原因在于Gm（）。在视频稳定中，为了使摄像机快速运动（例如，由快速平移或场景转换引起），不适当的平滑程度可能会导致过度裁剪，如图7所示。在这种情况下，摄像机会快速平移，并且高斯平滑（第二行）会导致相机路径明显偏离其原始路径，如顶部左图中的虚线所示。 第二行显示的相应帧将需要大幅度裁剪。我们的自适应项Gm（）在一定程度上保留了突然的摄像机运动。我们的自适应平滑处理（下一行）的结果产生的裁切更少。

为了测量相机运动，我们使用从相机姿态C（t）提取的平移分量µx（t），µy（t）的变化，即| µx（t）⇒µx（r）|。  + | µy（t）⇒µy（r）|。 帧平移µx（t），µy（t）可以描述实际上的大多数摄像机运动，除了围绕主轴的平面内旋转或缩放。

裁剪和失真控制

上面的自适应项ωt，r可以给我们一定的控制裁剪和失真的能力。 但是，用户可能希望严格控制裁剪率和失真。 原则上，我们可以制定约束优化来解决此问题。 但是它可能太复杂而无法解决或复制。

在这项工作中，我们采用一种简单但有效的方法-自适应地调整每个帧的参数λt。 我们首先使用全局固定λt=λ（经验设置为5）运行优化，然后检查每个帧的裁剪率和失真。 对于任何不满足用户要求的帧（裁剪比或失真小于预定阈值），我们将其参数λt减小一个步长（1 /10λt），然后重新运行优化。 注意，根据等式6，较小的λ将使优化路径更接近原始路径，从而减少了裁剪和失真。 重复该过程，直到所有帧都满足要求为止。

我们从翘曲变换B（t）= C 1（t）P（t）测量裁剪率和失真。  B（t）的各向异性缩放可测量变形。 可以通过B（t）的仿射部分的两个最大特征值之比来计算[Hartley and Zisser man 2003]。 我们使用B（t）计算原始视频帧和稳定帧的重叠区域。 裁剪比率是该区域与原始帧区域的比率。 在我们的实验中，我们要求所有示例的裁切率均大于0.8，并且失真得分均大于0.95。 原则上，我们可以通过B（t）中的两个透视分量进一步测量透视失真。 但是我们凭经验发现它们与仿射成分相比总是太小，不包含它们。

 

4.2优化捆绑路径

 

我们的运动模型会生成一堆相机路径。如果独立优化这些路径，则相邻路径的一致性可能会降低，这可能会在最终渲染的视频中产生失真。因此，我们通过最小化以下目标函数来对所有路径进行时空优化

其中N（i）包括网格单元i的八个邻居。

第一项是公式5中每个单路径的目标函数，第二项强制相邻路径之间的平滑度。 该优化也是二次的，并且可以通过求解大型稀疏线性系统来获得最佳结果。同样，我们的解决方案通过基于Jacobi的迭代来更新[Bron shtein and Semendyayev 1997]：

其中γ'= 2λt∑r∈Ωt，r = t wt，r + 2N（i）-1。

我们通常会迭代20次以优化相机路径

在优化过程中，由于不同的单元格具有不同的运动，因此在单个单元格上评估了运动自适应项Gm（·）。 相比之下，λt是从整体路径确定的（通过合并变形前的整体单应图生成），因为它控制了整体裁剪和失真。然后，我们使用λt优化所有像元中的相机路径。

结果综合

经过路径优化后，我们通过Bi（t）= C 1 i（t）Pi（t）计算每个单元i的翘曲矩阵Bi（t）。 然后，我们将Bi（t）应用于在第t帧处扭曲第i个单元以生成最终的输出视频。 通常，直接应用Bi（t）会产生良好的结果。 这是因为我们的运动估计可确保原始路径的一阶平滑度。 此外，公式8中的捆绑式优化要求附近的优化路径相似。 因此，Bi（t）通常大部分时间都可以满足平滑度的要求。 有时会出现轻微的变形（例如，接缝宽度约为1个像素），在这种情况下，我们会执行双线性插值法对其进行修复。

4.3校正滚动快门效果

我们的捆绑路径模型可以自然处理卷帘快门效果，而无需预先校准。 我们的方法的原理类似于[Grundmann等人.2012]。 我们的系统会在确保视频稳定的同时进行卷帘快门校正。 在摇晃的视频中，卷帘快门会引起空间变化的高频抖动。 在平滑相机路径时，我们会同时纠正因相机震动而引起的滚动快门效果和其他抖动。