读书笔记02--数据结构与算法分析：树以及C编程实现

一、树

我们知道、前一章节实现的表、栈、队列都是都是一种线性结构，不管你是使用数组实现还是链表实现这些数据结构。线性结构对于少量的数据也许很快，能满足你的要求。但是若遇到大量的数据时，访问时间就太慢了！

而树这种数据结构，其大部分操作的时间为O(logN)，树就是一些节点的集合。如下图所示，这棵树是N个节点和N-1条边的集合，其中节点A叫做根节点，每条边连着子节点和父节点，而除了根节点之外，所有节点都必须连着一个父节点。

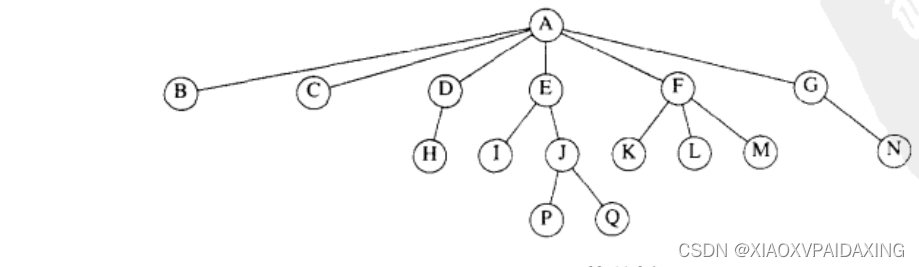
如上图所示：A为根节点，是BCDEFG的父节点，同时D为H的父节点，E为IJ的父节点，F为KLM的父节点，G为N的父节点，最后J为PQ的父节点。反过来说也可以，比如PQ都是J的子节点。另外，没有子节点的节点叫做树叶。
关于路径：从节点n1到节点nk的路径，就是n1,n2,…nk这个序列，要求1<=i<k时，ni是ni+1的父节点。满足这个的叫做n1到nk节点的路径，也就是所谓路径必须沿着子辈方向下去。比如上图，节点E到P的路径，就是E,J,P这个序列。
关于深度：节点ni的深度为根节点到ni节点的唯一路径的长。比如节点P的深度，就是序列A,E,J,P的路径的长=3。而根节点A的深度=0。
关于高：就是ni到一片树叶的最长路径的长。比如节点E，其深度=1，高=2；而节点J，深度=2，高=1；所有树叶的高=0。
所以，一棵树的深度就是它最深的树叶的深度，而一棵树的高就是它的根节点的高。所以一颗树的深度=它的高。

1、树及其实现

树的典型用法之一就是目录，如下图所示为UNIX文件系统的一个典型目录：

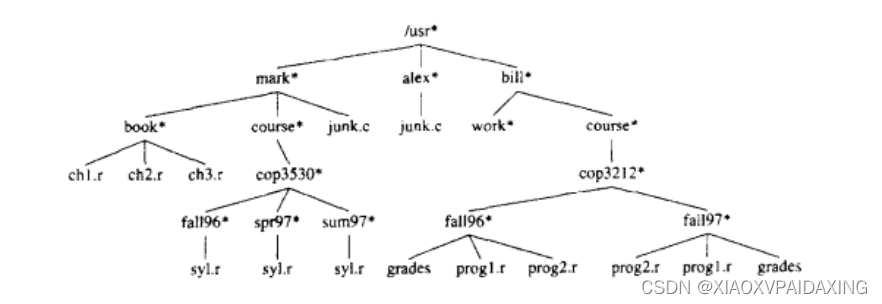
如上图所示，其中带*号的都表示为目录名，不带*号的都表示是具体的文件名。所以，从最上边的根目录看，/usr*是根目录，其下有3个儿子，mark*，alex*，bili*，都带*说明都是目录名。然后我们看路径"/usr*/mark*/book*/ch1.r"，除了/usr*外的/斜杠都表示一条边，而最后的ch1.r就是具体的一个r后缀的文件名。

实现目录的操作：

C编程时，由于路径是从上到下的，也就是指针应该至少不能往上走，那么如果要实现前一张图那种树状，就得在父节点多弄个几指针留着，当有子节点添加时，就将该指针指向添加进来的子节点，从而最终实现前一张图所示的树状。但是，子目录的加入很随机啊，指不定什么时候就像创建一个子目录，也有可能创建很多个，那么你每个节点到底要预留多少个指向子节点的指针才够用呢？而且预留的多了，但如果不用或只用一两个，那么这个目录岂不是占用很大空间。所以，编程时我们不像上面那个那样做，因为基本上要预先留多少多少空间的这种编程方式都不会太灵活且死板，而且容易浪费空间。
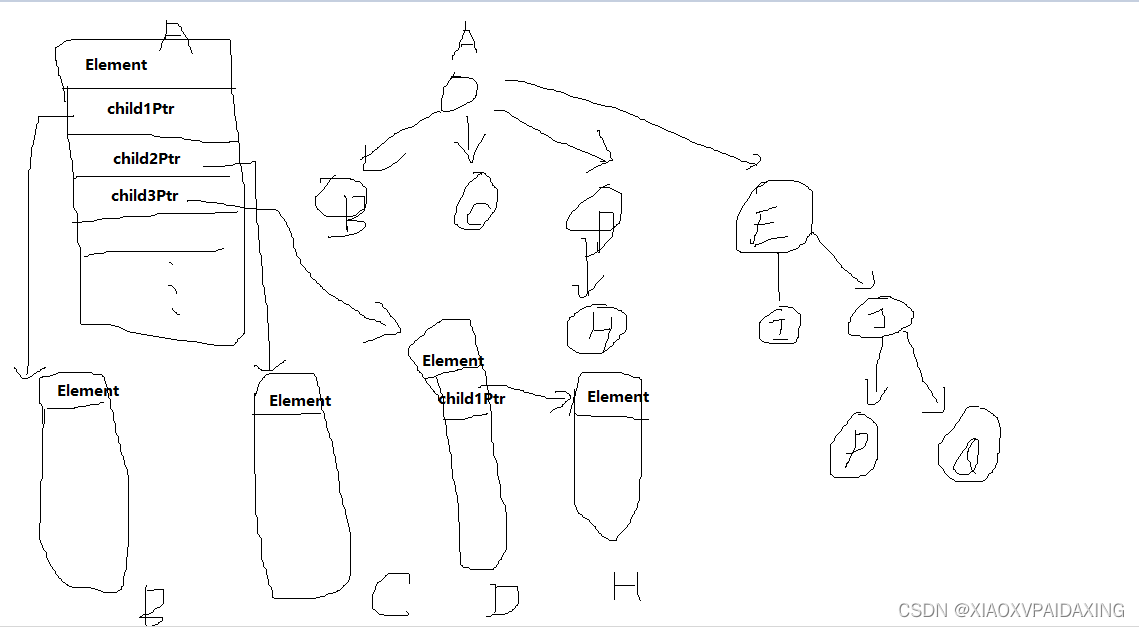
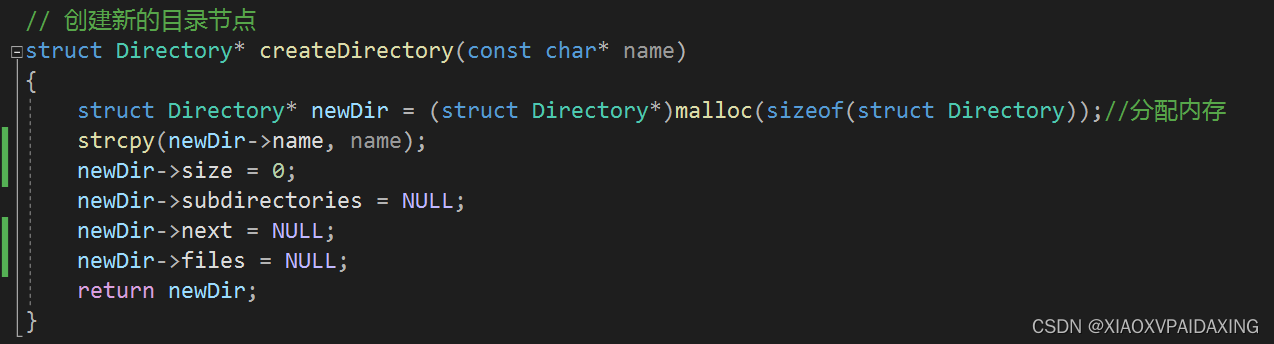
那么要怎么做呢？如下图所示，书里给了解决方法，就是不预留，每个节点只保留一个指向第一个子节点的和一个指向兄弟节点的指针就可以了。

如下图所示：图中向下的箭头代表指向子节点的指针，而水平横向的指针代表指向兄弟节点的指针。那么处在同一水平面的就是兄弟节点，它们并不都与父节点相连，而是直接由兄弟节点Next指针连起来。处在不同水平面的就是父子关系了。比如下图的意思就是，节点BCDEFG之间是兄弟节点，同时它们都是A的子节点，其中节点B时A的第一个子节点。这样，按照下图来进行C编程，不仅能实现树状结构，而且增删灵活，不浪费空间。

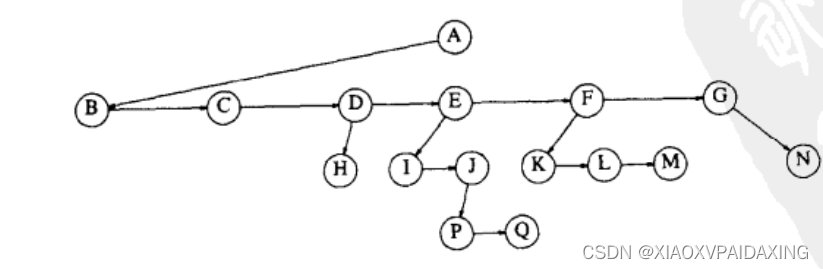
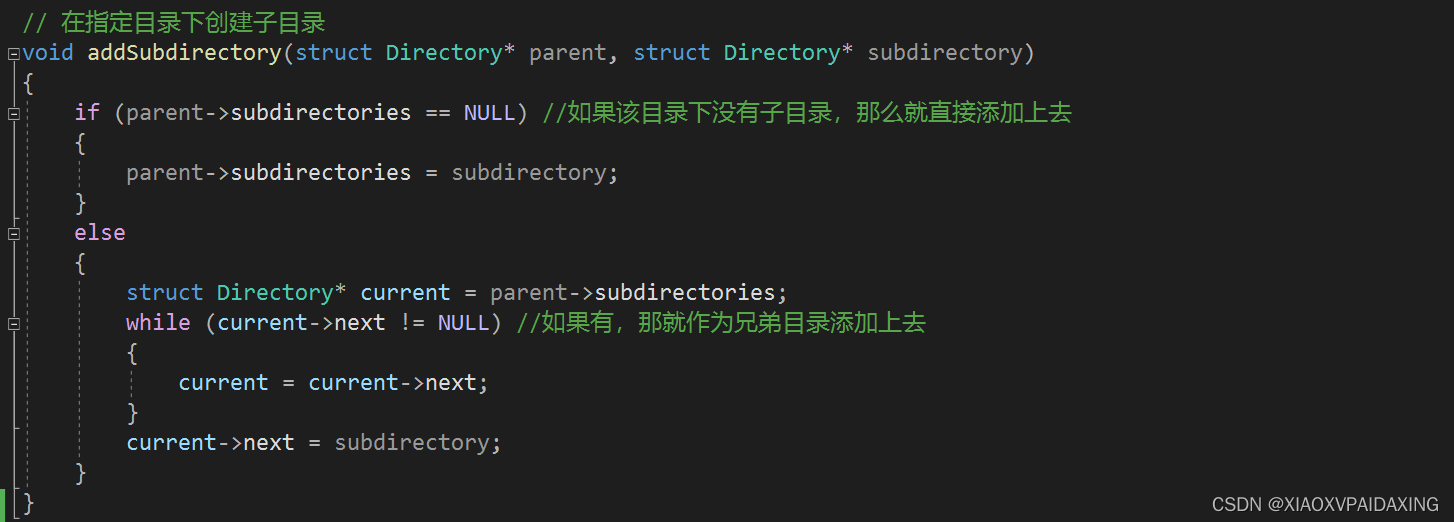
具体C编程实现如下所示：



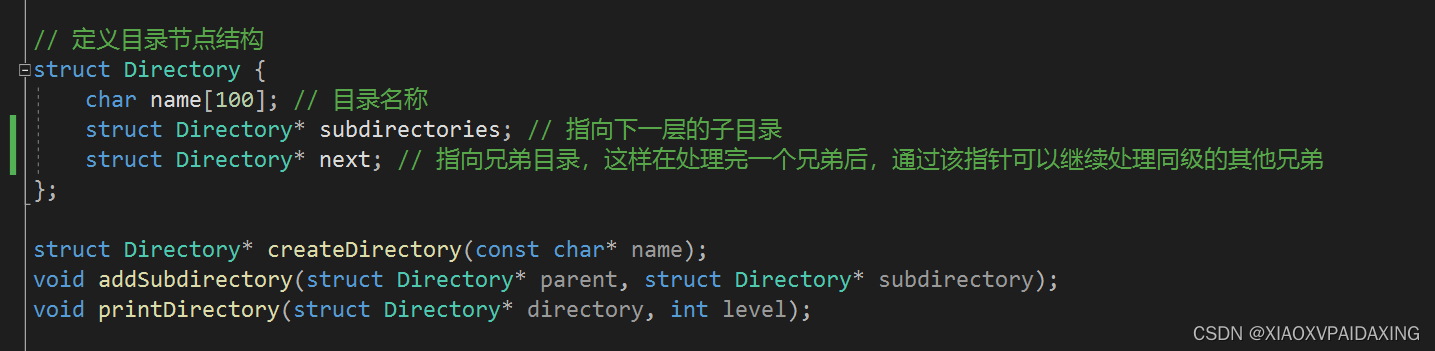
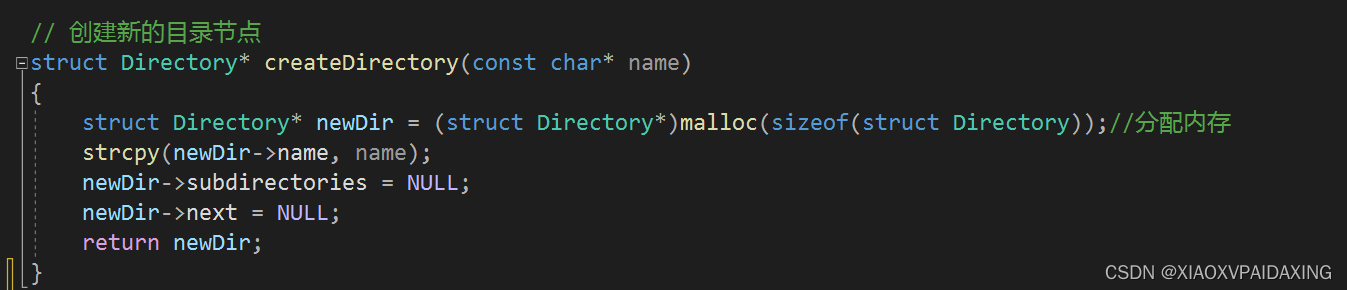
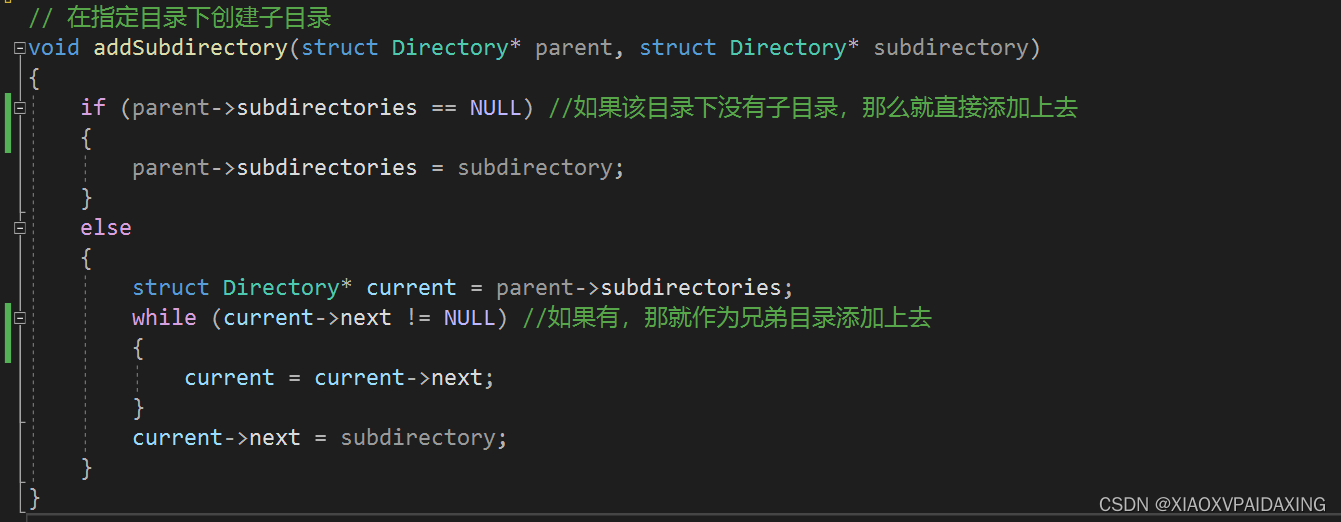
如上图所示，如果所选目录下没有子目录，也就是子节点sub指针为空，那就直接指向新节点就添加上了，如果由子目录，那么就共同sub获取该子目录，再找该子目录的Next指针，直到Next没有节点指向，那么就把新节点添加进来。

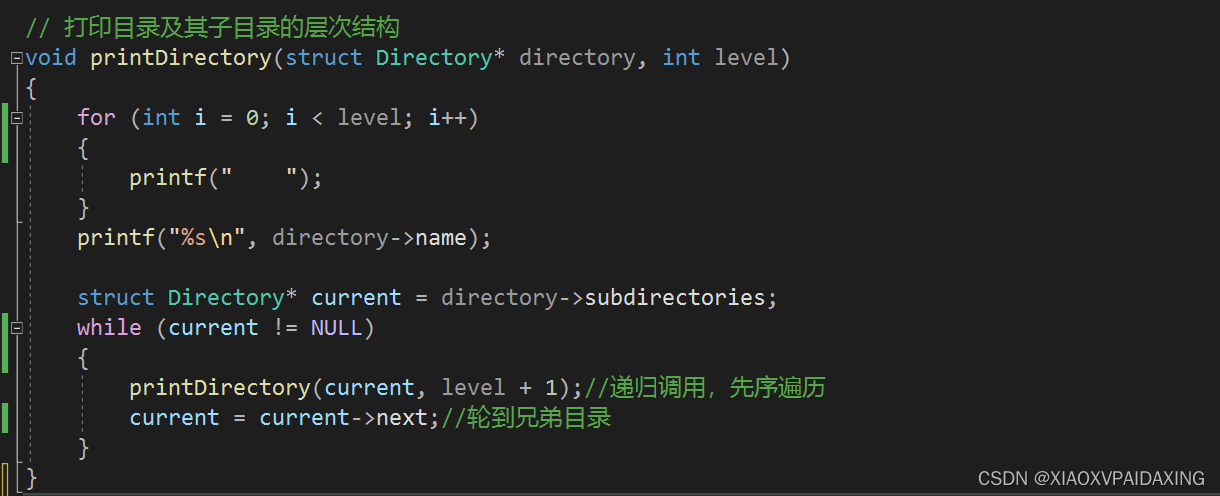
程序写完了，那么来看看效果如何：

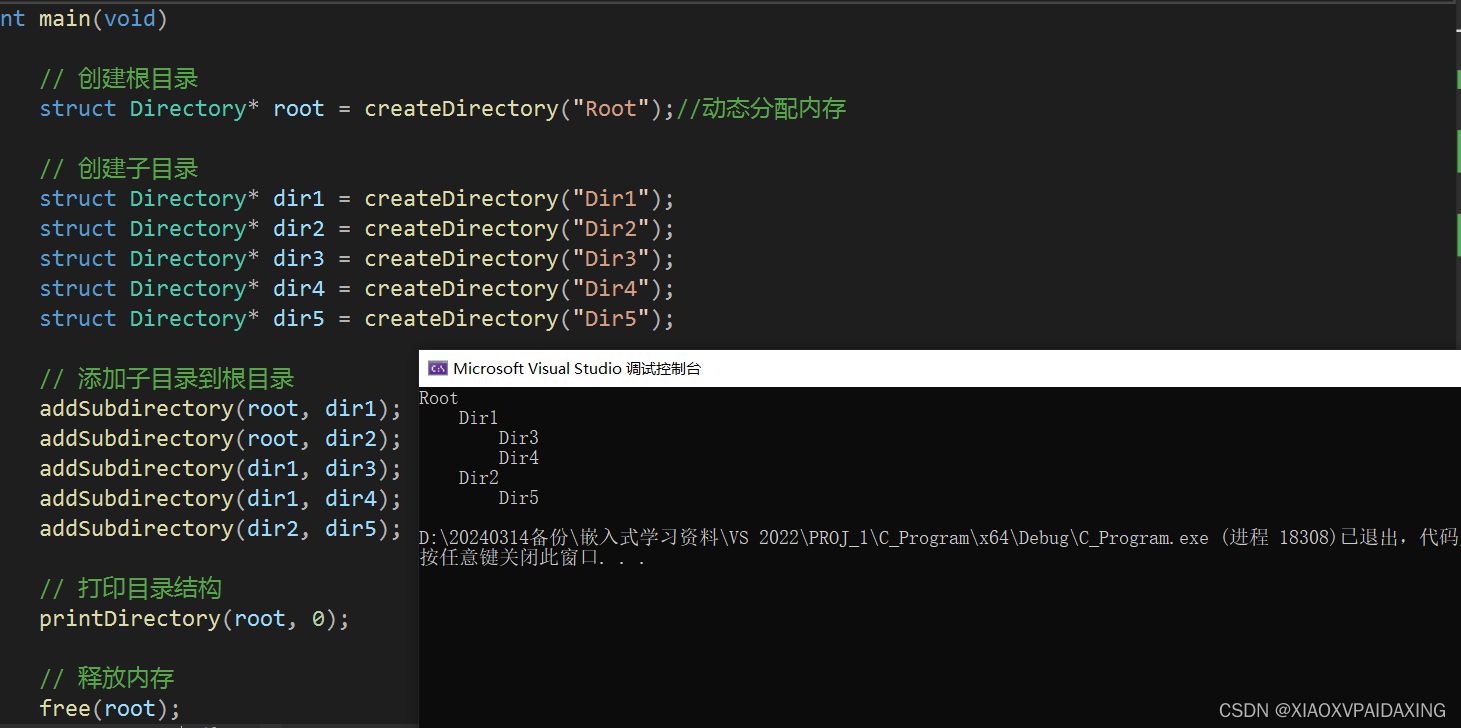
如上图所示，可以看到控制台把目录打印了出来，而且是根据不同的深度，对应提供不同的空格键缩进，也就是同一深度的打印在同一缩进的列上，从而显示出这样的目录关系。
实现上述目标的核心在于递归printDirectory的使用，函数里所遍历各个目录的策略叫做先序遍历。所谓先序遍历，就是对节点的处理，比如打印节点的名字，这个操作是先于它的子节点（如果有的话）被操作处理之前的。分析这个函数也知道，是从上到下，对根节点先打印名字，然后去获取其非空子节点，递归调用，直到遇到NULL才终止这条分支的处理，接着找该非空子节点的兄弟节点，继续同样的操作，直到处理完根目录下的所有非空子节点，也就是Next终止在NULL上。
又比如下图所示，打印目录dir1下的（包括dir1）的所有目录：

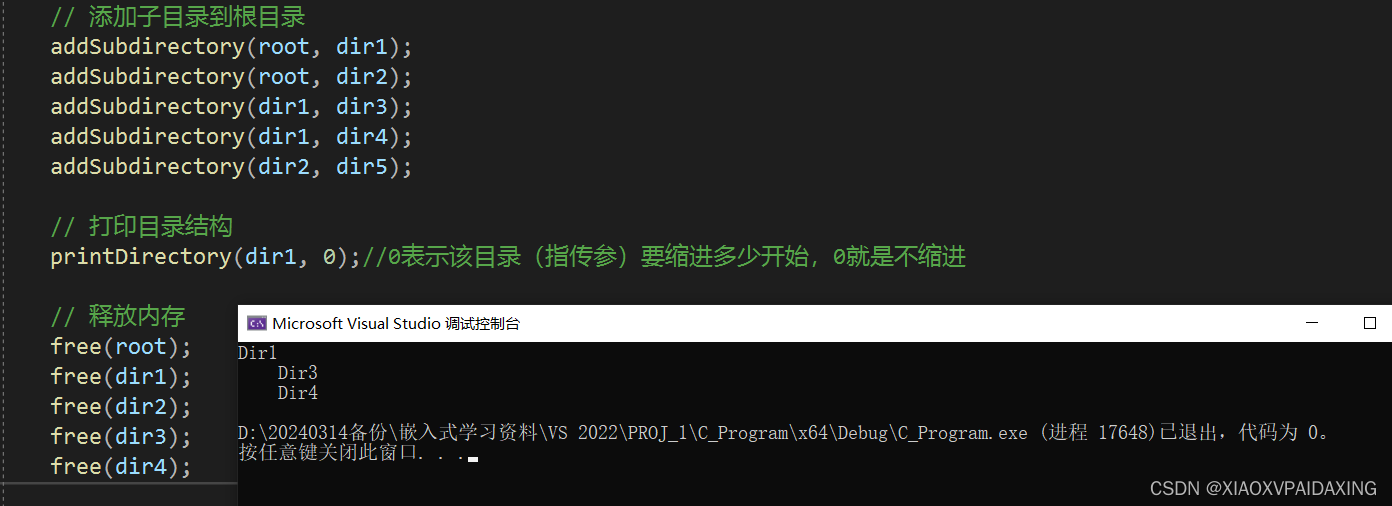
还有一种叫做后续遍历，顾名思义，对子节点的操作要先于本节点进行，也就是都处理完儿子分支再处理本节点，如下图所示：

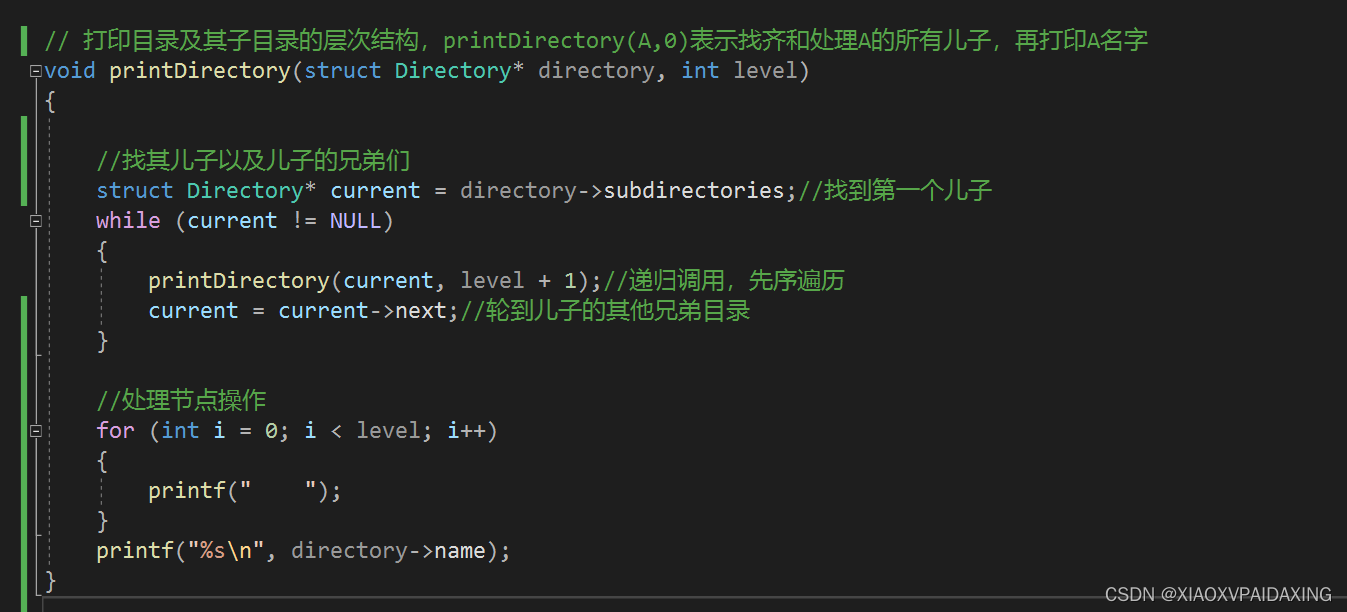
看一下运行效果，如下图所示，很显然，程序会对一支儿子分支一直找，直到找到树叶并处理了树叶以及树叶的兄弟才会回来上一层处理，就这样依次回到上层处理节点（打印名字）。所以可以看到名字的打印是和先序遍历反着来的。

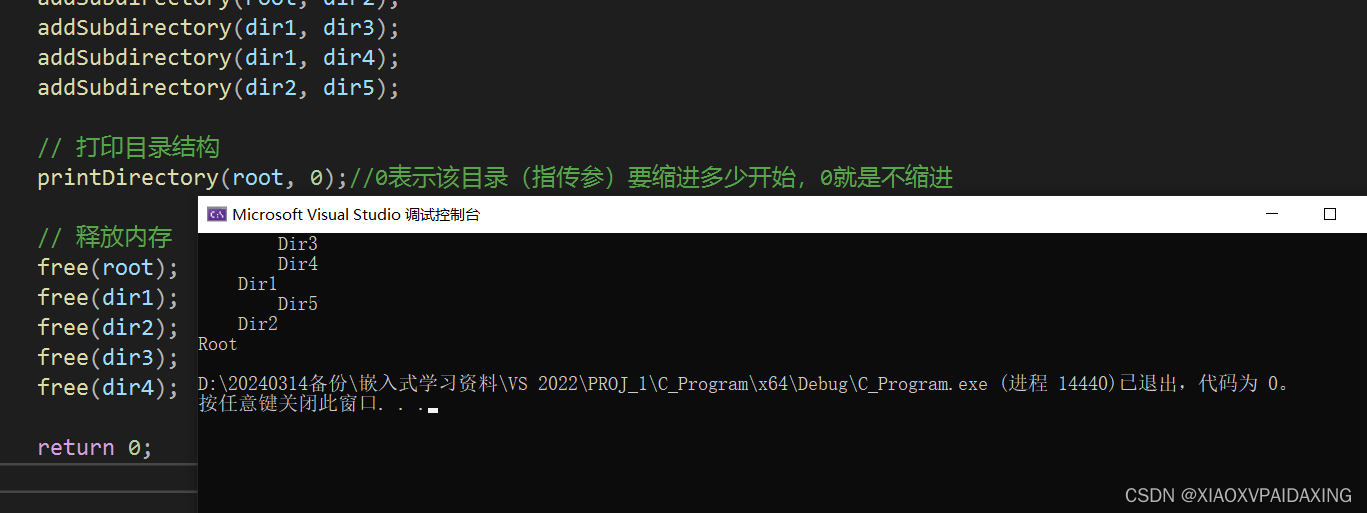
那么后续遍历，有什么好处吗或用处吗？其实可以用来计算文件各个目录的大小，利用后续遍历进行累加，很轻易就能得到各层目录占用空间的大小。C编程如下所示：需要再定义一个文件节点的结构体






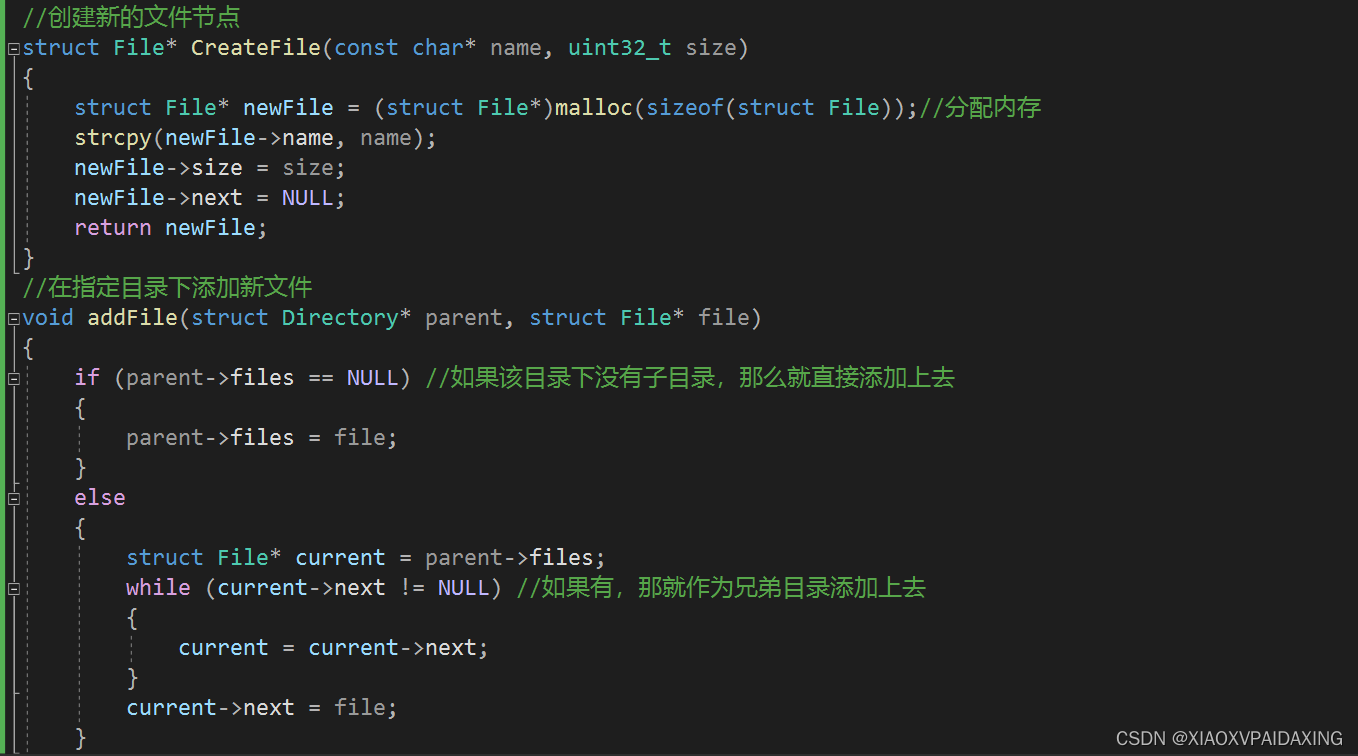
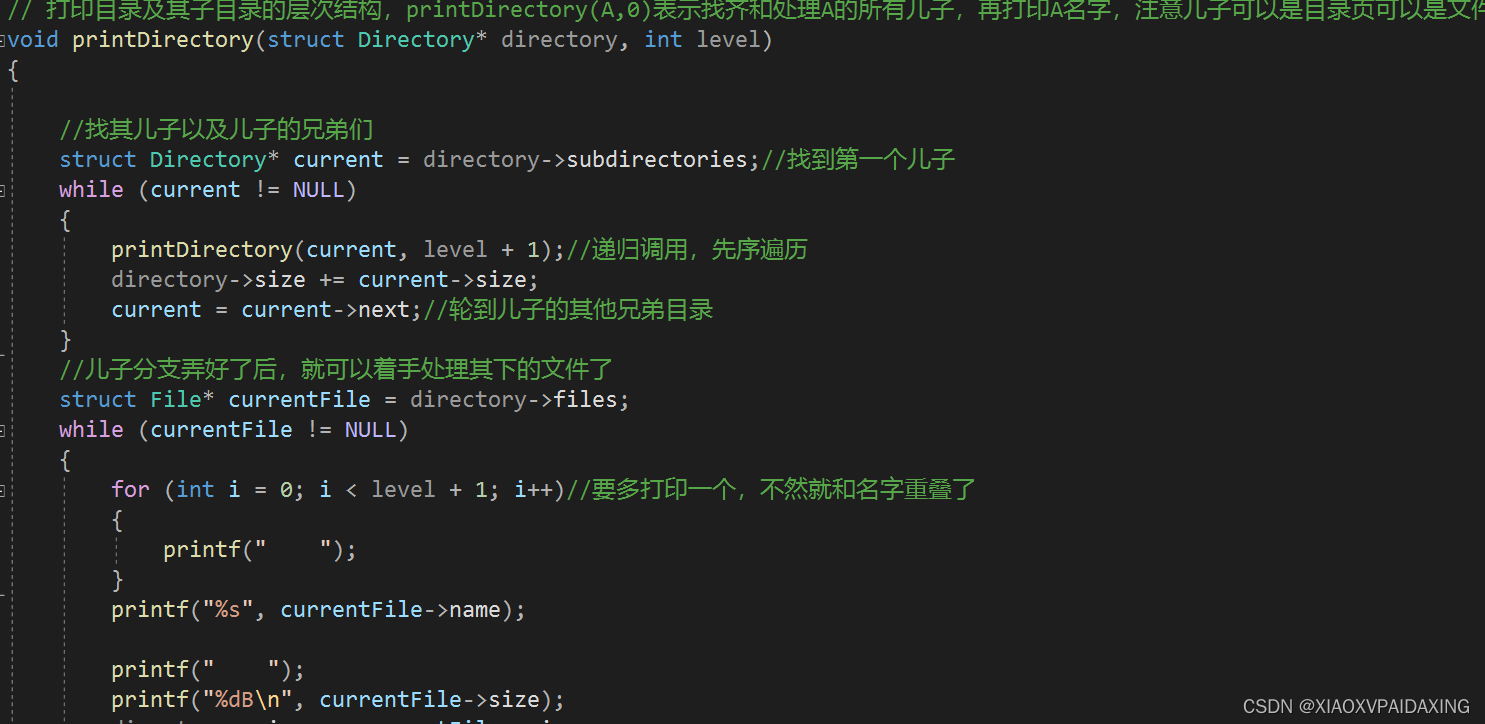
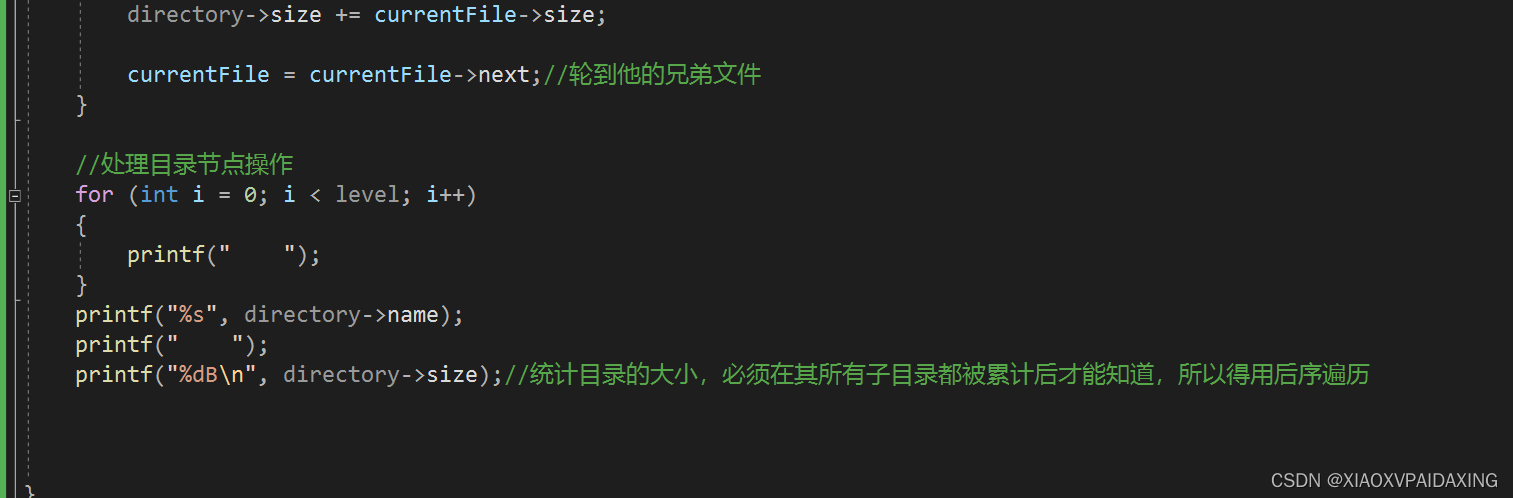
程序写好了，我们来看看运行效果，看看能不能正确统计每个目录的空间大小：

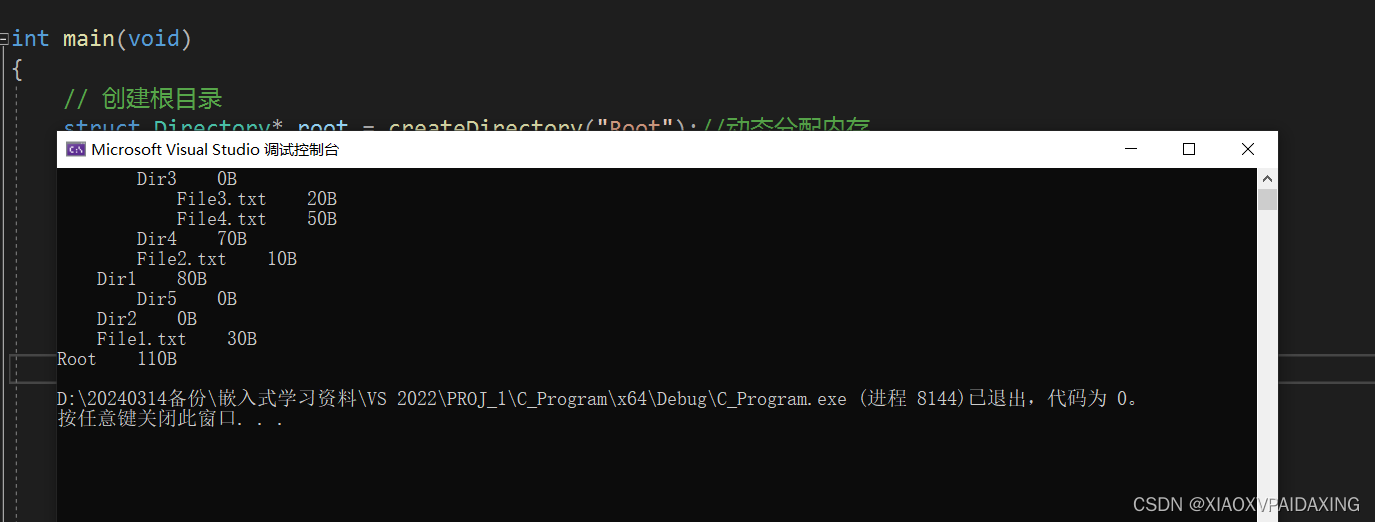
如上图所示，为后续遍历，因为统计每个目录大小必须得在其下的子目录和文件都被统计了之后才知道该目录的大小。从上图中可以看到，不管是目录还是文件，最后的统计都正确表示了出来，比如目录Dir4的大小为70B，是因为该目录下瞎两个文件file3.txt，file4.txt，一个20B，另一个50B，所以加起来就是目录Dir4的大小70B。其它的可自行查验，这里就不一一展开了。

2、二叉树（binary tree）

二叉树也是一棵树，只不过规定了其每个节点不能多于两个儿子。比如下图，其中TL或TR都可能为空，反正图示root节点不能下辖多余两个子节点就行了。

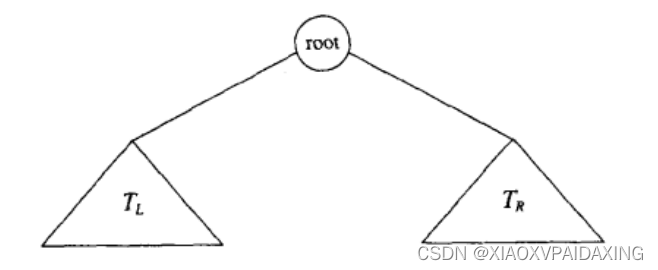
因为这里的二叉树人为规定了了最多两个儿子，所以不像前面的树介绍那里那样，儿子数量不定长的导致不好直接预留很多指针空间来直接指向所有加入的儿子。但，二叉树不同了，最多两个，那么直接使用两个指针就行了，不用担心空间浪费以及预留多少指针，或者像前面的编程那样去优化处理。接下来看看二叉树的C实现。

二叉树由于它的特性，所以如下图所示，直接使用两个指针即可。

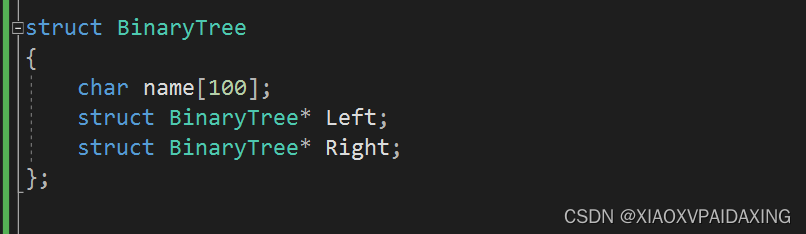
有了前面对树的编程经验，其实更加简单二叉树实现起来只会更加容易：


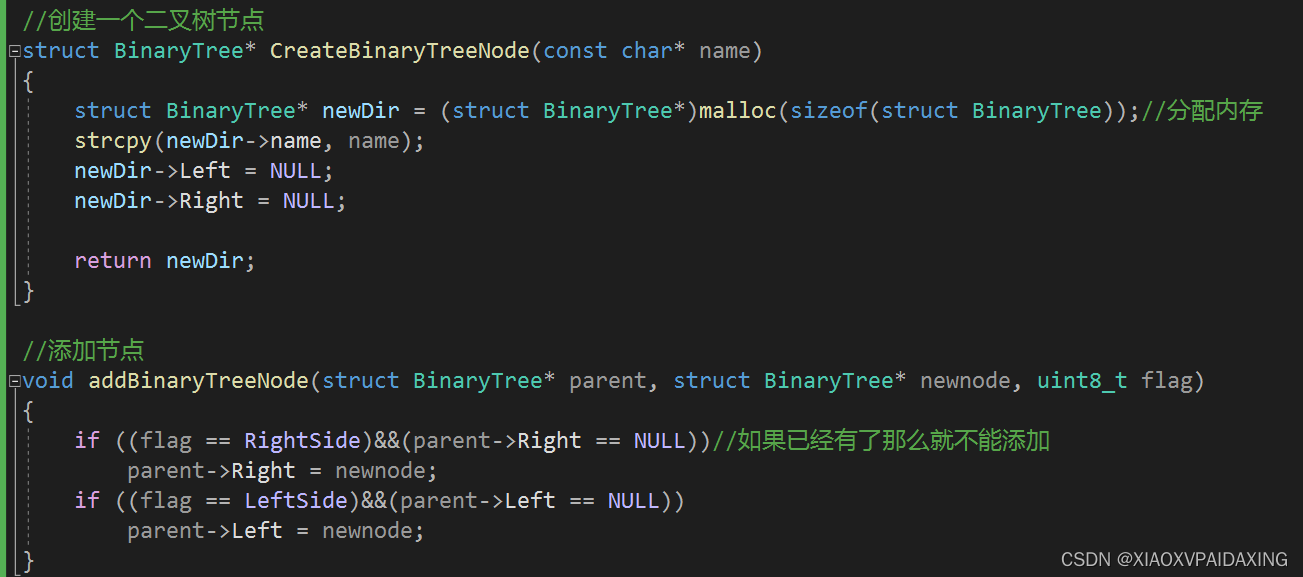
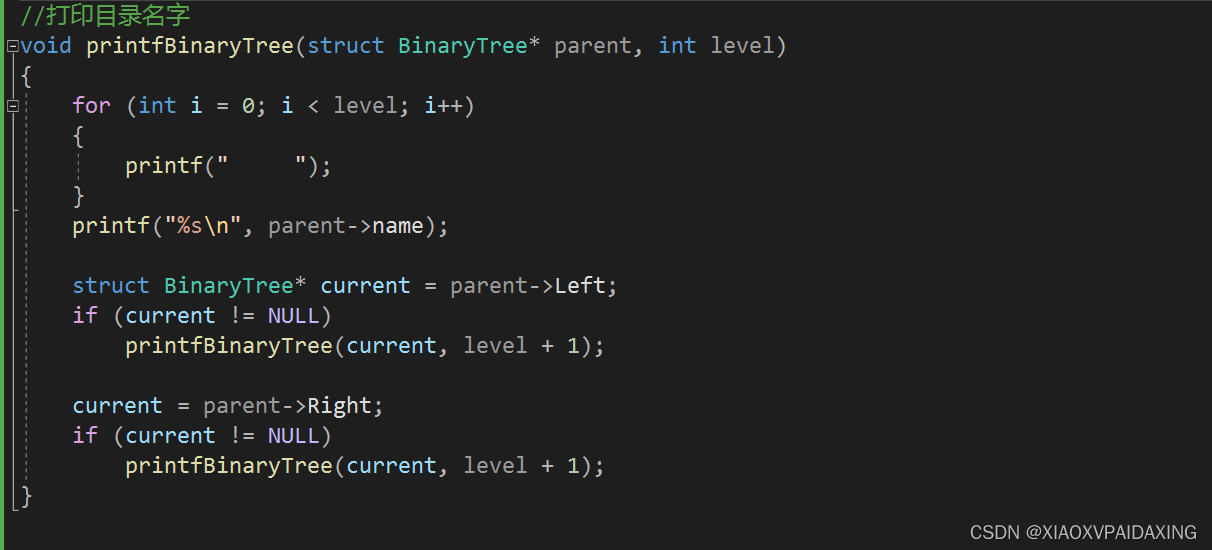
程序写好了，测试一下效果，如下图所示，同样也是用来做目录：可以看到效果也可以，只不过每个分支最多两个而已。
先序遍历如下：

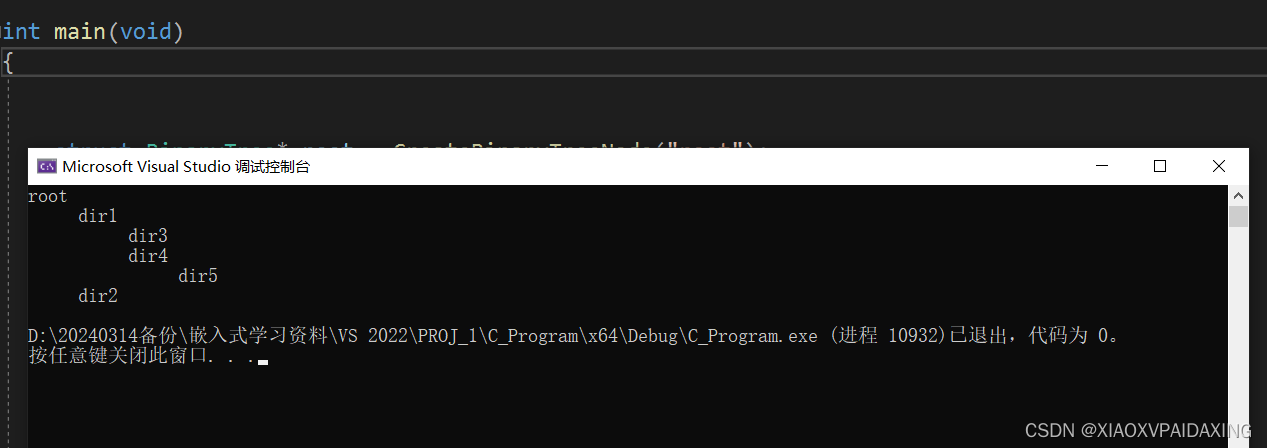
后续遍历如下：

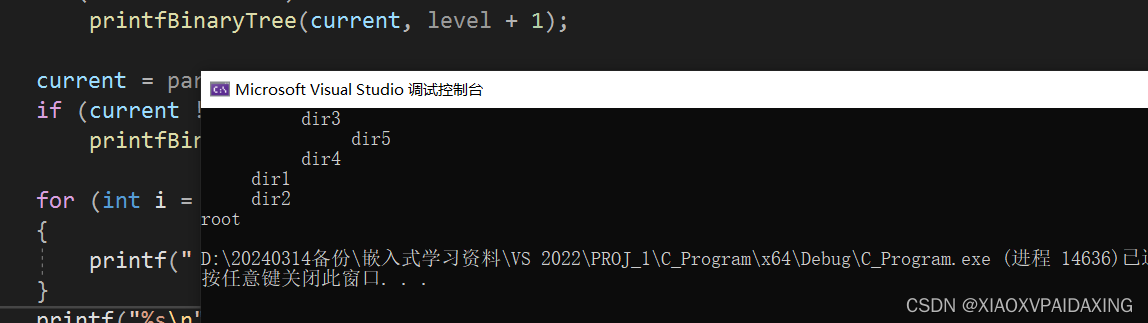
其实通过上面的编程也可以发现，二叉树并不适合做目录的应用，因为它把子节点数固定了。
关于二叉树的应用，主要用于编译器的设计，而非搜索或者目录查找之类。所以接下来看看二叉树应用于表达式的计算。

2.1 二叉树应用–表达式树实现

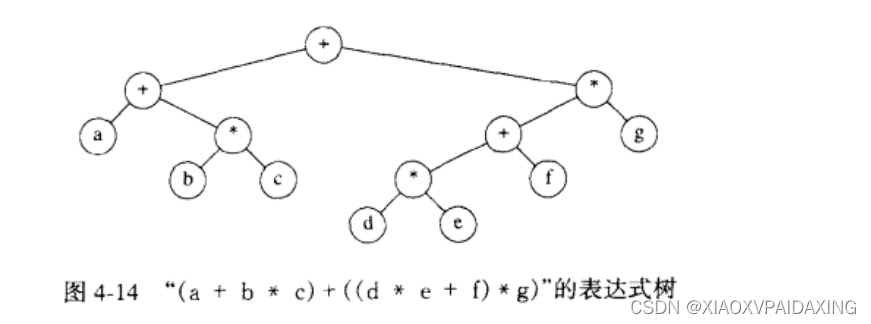
使用二叉树构造的表达式树如上图所示，我们计算的时候看左子树=a+(b*c)，而右子树 = (（d*e）+f)*g，然后整个树=左子树+右子树=（a+(b*c)）+（(（d*e）+f)*g）。怎么通过递归来编程实现这种运算，有一只策略叫做中序遍历，就是先左分支，再回来处理本节点，最后右分支，这样一来就不是如同先序或者后续那样了，而是子节点和父节点的处理混杂在一起。使用这种策略是因为这个表达式树的特点，因为除了树叶外，都是运算符，要把左右节点的数据通过中间的运算符计算起来。
我们可以分别试一下这几种策略，看看出来时什么效果：
中序：(a+(bc）)+((de)+f)*g，这种遍历很容易记忆，因为和我们人的计算思路相同；
后序：就是左、右、节点，abc*+de*f+g*+，这种也叫做后缀表达式；
先序：就是节点、左、右，++a*bc*+*defg，这种也叫做前缀表达式，不太常用。

下面将对一个后缀表达式输入，构建一个二叉树，如下所示：
ab+cde+**，我们手动绘制的结果如下所示，

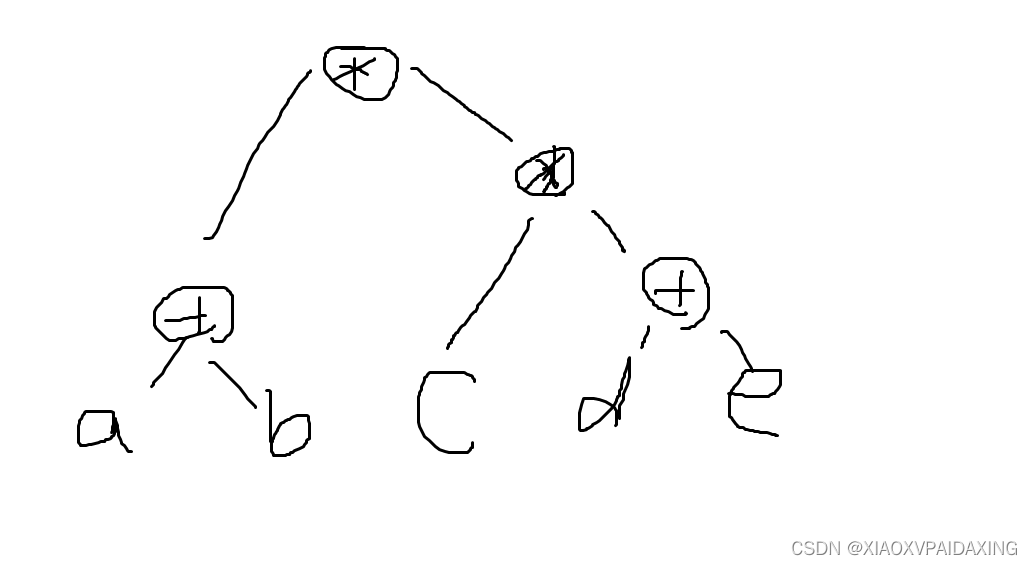
再反过来验算一下该表达式树，确实没问题。
C编程：
1、创建一个空堆栈。
2、扫描后缀表达式中的每个字符：
如果遇到操作数，创建一个叶节点，并将其推入堆栈。
如果遇到运算符，从堆栈中弹出两个节点作为该运算符的右子树和左子树，并创建一个新节点，将新节点推入堆栈。
3、最后，堆栈中剩下的唯一节点就是表达式树的根节点
看看程序写好后的运行效果，如下图所示：可见，成功把后缀表达式转换成了表达式树，并根据表达式树打印了我们理解起来更加容易的中序表达式。

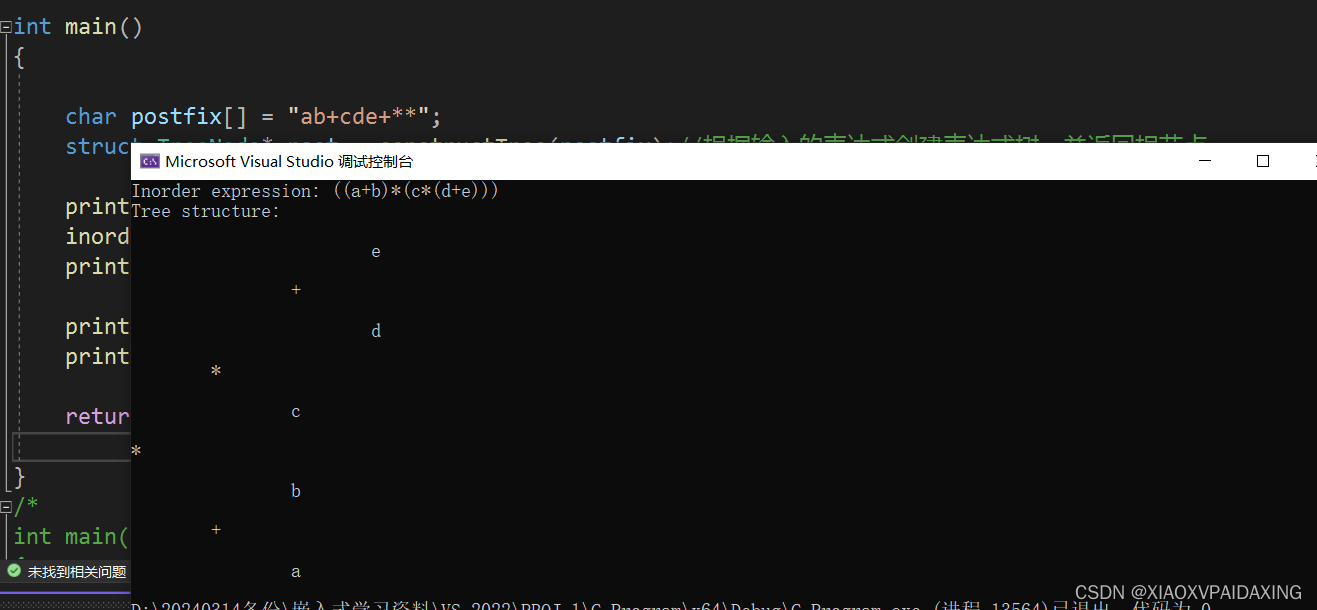
我们知道，将表达式树打印出前缀或后缀或中序表达式都很简单，只需换一下打印顺序即可。所以这点是将输入的前缀或者后缀或者中序表达式转换成表达式树，这里的思路已经实现了将后缀转换成表达式树。
而要做前缀，其实也很简单，在实现后缀转换的基础上，对输入的表达式从后往前一个个读取字符不就好了吗！
至于常规的中序，会复杂一些，因为中序表达式无法直接从左到右或从右到左扫描并构建树（这一点不像前缀或后缀那样通过先后顺序就知道怎么算怎么结合），要考虑运算符优先级，
比如，a+b*c+d*e+f*g这段计算机就不知道怎么去解释，所以实际上还需要(a+(b*c）)+((d*e)+f)*g这些括号来帮助优先级划分。
所以，中序表达式在计算机科学中更适合人类阅读和理解，但在编译器中处理起来相对复杂。后缀表达式和前缀表达式都是没有括号的，操作符位于操作数之后或之前。与中序表达式相比，后缀表达式和前缀表达式更容易用计算机算法进行解析和计算，因此在编译器中更常见。后缀表达式将操作符放在操作数之后，例如：2 3 + 表示 2 + 3。前缀表达式将操作符放在操作数之前，例如：+ 2 3 表示 2 + 3。这两种表达式可以通过栈结构或递归算法轻松地转换为表达式树和计算。至于中序表达式的C编程，有兴趣的就自己去实现一下吧。

2.2 二叉查找树

二叉树的一个非常重要的应用就是它在查找中的使用。要想利用二叉树构建二叉查找树，要求是的每个节点X的左子树的所有节点值小于X的值，而右子树的所有节点值要大于X的值，这样的二叉树就是二叉查找树。

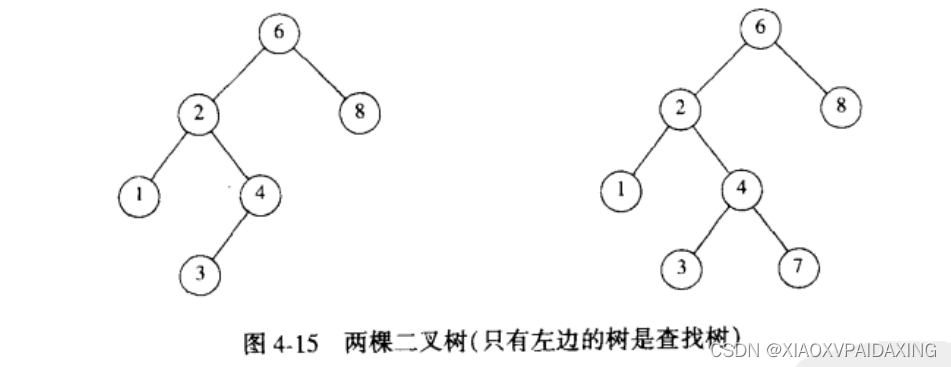
如上图，右边的树的7值位于6的左子树，而它大于6所以这不是二叉查找树。
既然是查找树，那就要实现查找树的ADT，我们看看书里对二叉查找树的编程思路如何实现：


可见它查找的思路是利用二叉查找树的特点，就是每一个节点，其左子树都小于该节点，其右子树都大于该节点。当对树T查找X时，如果X小于该节点的值，就递归左子树，若大于那就递归右子树，到最后要么能找到=X的节点，要么NULL没有找到符合X的节点。

如上图，所以如果要找最小元，那一只往左子树找就行了，而如果要找最大元，那就一只往右子树找就行了。

而插入操作也很简单，先查找，小于节点就往左子树递归插入，大于节点就往右递归插入，如果本身值就是那就直接返回不用插入了，直到为NULL时就可以动态创建MALLOC一个新节点保存X，然后往回T。因为二叉查找树的特点，如果不是重复的元素，那么一定是在节点的NULL子分支插入。

接下来是删除操作，这是比较麻烦的，如果要被删除的是树叶，那么可以立即删除，因为它没有子节点，但如果不是，那么它的子树要怎么处理？
如果要被删除的节点具有一个儿子，如下图所示，要删除4，那么先找到4，保存4的指针，然后修改4的父节点2的相同指针指向3，修改完成后，再根据先前保存的指针删除掉4节点。

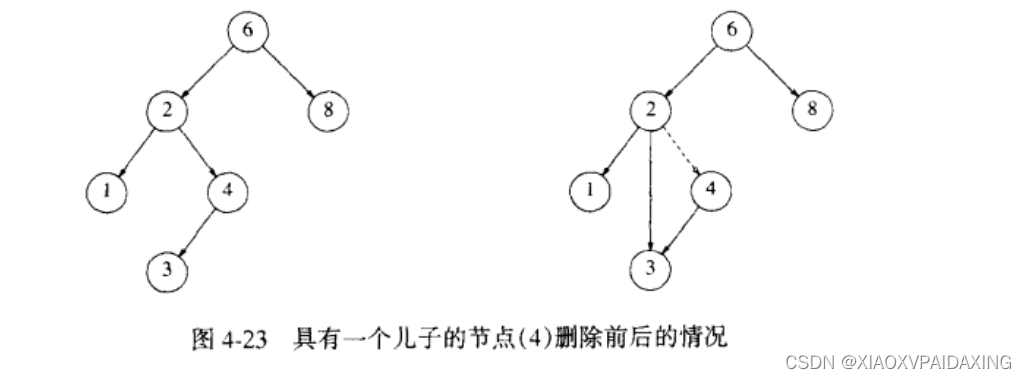
而如果有两个儿子呢？如下图所示，要把节点2删除，办法就是找一个来填补2位置的空缺，找谁呢？可以找该节点的左子树的最大节点，这样也符合二叉查找树，也可以找该节点的右子树的最小节点。这里选择后者为例，找到节点2的右子树的最小值3，将节点2的值修改为节点3的值，然后递归调用删除函数，这时节点3的删除是前面的具有一个儿子的节点的删除了，因为右子树的最小节点不可能有左儿子，不然它就不会是最小那个，如果连右儿子都没有，那删除更加容易。

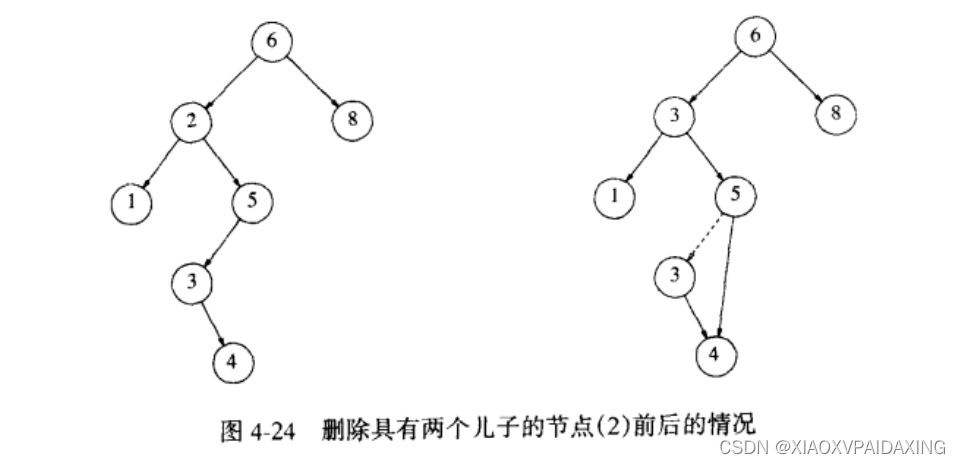
如果删除次数不多，或者删除重复值时还可以采用懒惰删除，就是节点增加一个频率指标，用来记录它出现的次数，而不是真的删除它，因为比如树很大时删除它比较耗时。

2.3 AVL树

AVL树就是带有平衡条件的二叉查找树，这个平衡条件要保证树的深度为O(logN)。为什么要搞带平衡条件的二叉查找树呢？因为在前面关于二叉查找树的实现中可以发现树的平均深度越大，我们对树进行插入和删除的操作的时间复杂度就越高，两者几乎成正比。在最坏的情况下，如果树变得非常不平衡，接近于一个链表，其操作时间复杂度将退化为 (O(n))（其中 (n) 为节点数），而不是原先的O(logN)。我们希望通过保持树的平衡，我们可以确保这些操作的时间复杂度保持在 (O(\log n)) 的范围内，从而大大提高了操作的效率。继续往下之间，先来弄清楚几个问题：
1、先探讨下什么是不平衡？
在一个二叉查找树中，不平衡指的是树的左右子树高度差异过大。具体来说，对于任何节点：若其左子树与右子树的高度差异超过某个阈值（通常设定为1），则认为该节点处于不平衡状态。
2、再探讨下为什么二叉查找树会失衡呢？
（1）、插入顺序：
当节点插入时，如果数据是有序或接近有序的（例如，插入顺序为1, 2, 3, 4, 5），树会变得非常不平衡，形成一个类似链表的结构，为O(N)。插入顺序对树的形状有很大影响。在最坏情况下，插入顺序会导致所有新节点都被插入到树的一侧，从而使树高度增长过快。
（2）、删除操作：
删除节点后，剩下的子树可能会变得不平衡。例如，删除一个带有唯一子节点的节点时，结构可能会变化，导致一侧子树比另一侧子树高很多。
3、最后探讨下不平衡会有什么影响？
（1）性能退化：
查找、插入和删除操作的时间复杂度与树的高度成正比。在理想情况下（树完全平衡），二叉查找树的高度是 (O(\log n))，其中 (n) 是节点数。但在最坏情况下（树完全不平衡，也就是链表状），高度会变成 (O(n))。因此，不平衡会导致操作效率从 (O(\log n)) 退化为 (O(n))。
（2）空间利用率低：
不平衡的树会占用更多的内存和栈空间，特别是在递归操作中，深度更大的树会导致更深的递归调用栈。一直递归或长时间深度的递归导致栈的空间急剧缩小。
（3）访问局部性差：
现代计算机系统中，缓存命中率对性能有显著影响。不平衡的树会导致较差的缓存局部性，因为需要访问的节点分布在更大的内存范围内，导致更多的缓存未命中。
4、如何解决二叉平衡树这种结构固有的不平衡问题？
当然是添加平衡条件，来保持树的平衡。具体怎么添加平衡条件，后续再讲。

下面这张图就是不断插入和删除操作后生成的二叉树，显然非常不平衡，平均深度大，原因可能在于删除操作中不断使用右子树的一个节点来代替被删除的节点，导致左子树比右子树深得多。

怎么去做平衡条件呢？
比如要求左右子树要有相同高度，如下图所示：

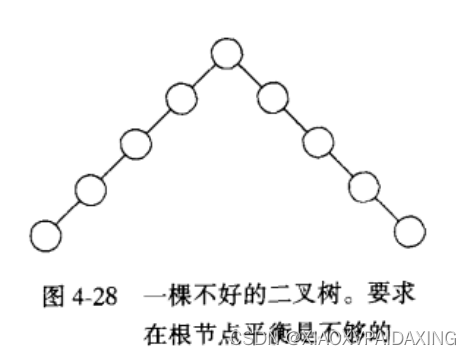
又比如，要求每个节点都必须有相同高度的左子树和右子树，虽然这个平衡条件保证了树的深度小，但过于约束无法使用。
那么来看看AVL树怎么做？它的定义是，每个节点的左子树和右子树的高度最多相差1的二叉查找树。如下图所示，左边是AVL树，右边的不是，因为根节点7的左边和右边高度相差为2>1，不满足平衡条件。

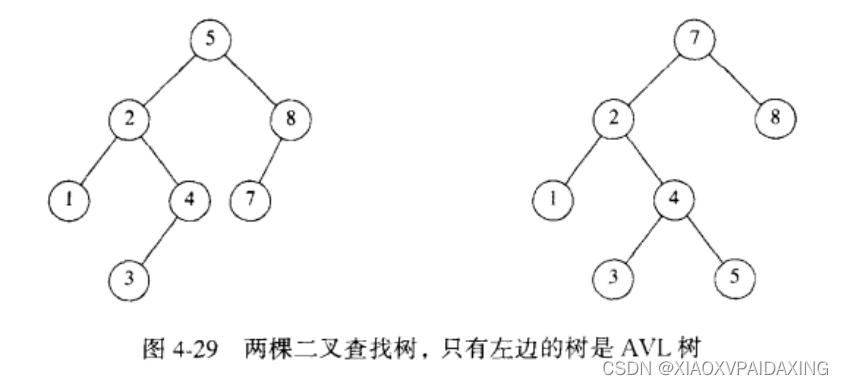
-----------------------------------------关于树后续补充来日继续-----------------------------------------------------------

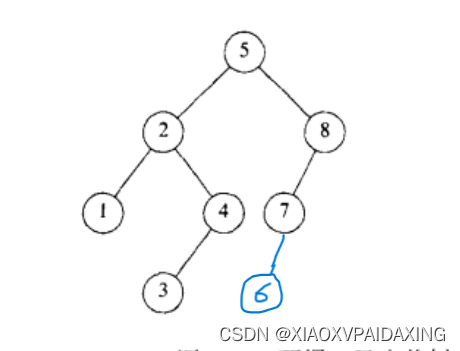
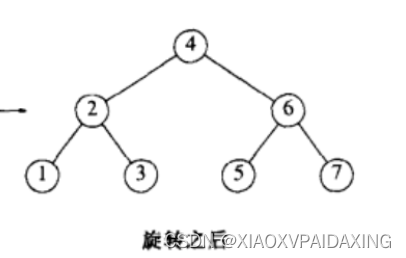
如果把6插入到这颗AVL树上，显然，会成为7的左节点，这样一来8节点的左右子树的高度就相差为2了，也就是说插入操作很可能会破坏了AVL树的定义。所以为了实现AVL树，我们会在插入操作后进行旋转操作，来重新恢复AVL树。
不平衡的情况有以下几种：
1、对左儿子的左子树插入一次；
2、对左儿子的右子树插入一次；
3、对右儿子的左子树插入一次；
4、对右儿子的右子树插入一次。
对于左-左或者右-右，可以通过单旋转的方法实现调整。对于左-右或者右-左情况可以通过稍微复杂双旋转来调整。
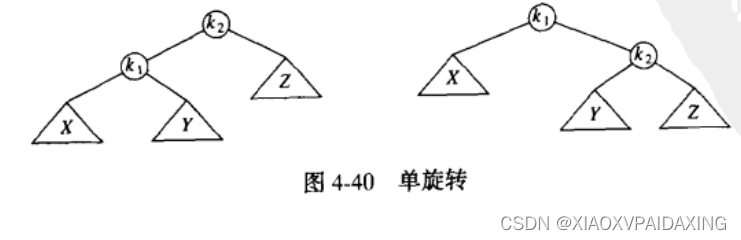
（1）单旋转
左-左

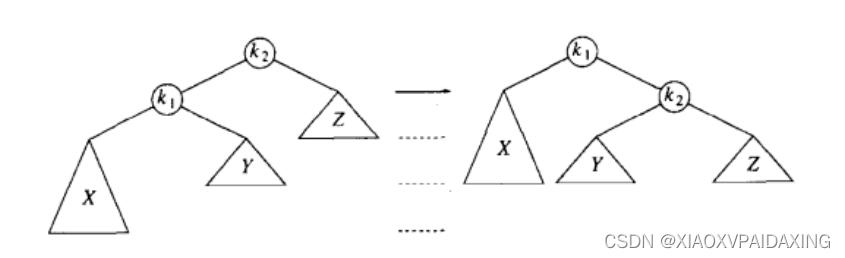
如上图，左边是二叉查找树，X在第四层，往上倒可以知道在根节点k2出现了不合符AVL的特性，因为k2的左子树的高度比右子树大2。那怎么通过单旋转来恢复根节点的AVL特性呢？书里说的也很形象，就是根节点k2出错，那就找根节点，而且是左边深了，那就抓住根节点的左子节点，往上拉而成为根节点，然后由于树的重力作用，k2就往下沉而成为k1的右节点，同时由于k1的原右节点的值Y是在k1和k2之间，所以就移动到k2成为k2的左节点，如此一来，旋转就完成了，如右边的图所示，就是完成旋转后的新的AVL树，为什么是AVL，因为旋转后，原本下沉的左子树被提上来的，经过调整后，各个节点都满足AVL条件。（旋转中，k2失去了左儿子，k1则新增了又儿子，而k1原本的右儿子y的值原本就处在K1k2之间，大于k1小于k2所以移植到k2成为左儿子）
右-右：

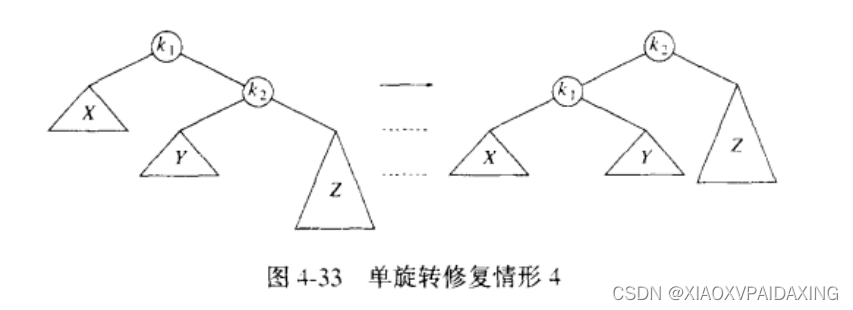
如上图，操作方式一样，根节点k1左子树和右子树相差2出现不平衡，而且右边下沉。所以将k1和k1的右节点作为本次旋转的目标。k2往上拎，然后k1就自然下垂成为k2的左节点，最后K2原本的左节点y的值因为介于k1和k2之间，所以移植到k1成为k1的右儿子。（旋转中，k1失去右儿子，k2新增左儿子，所以原本k2的左儿子因为本来就介于k1k2中间，所以就要移植成为k1的右儿子）

针对单旋转，举个例子：

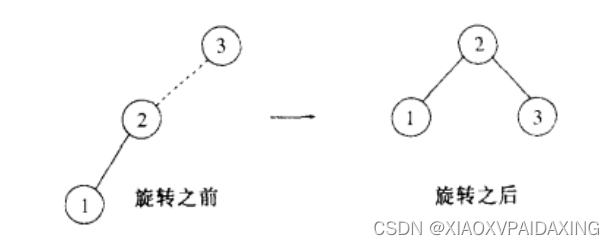
如上图所示，左边的二叉查找树显然在节点3处不平衡，左边下沉，所以把节点3和节点3的左儿子作为旋转的目标（就是虚线连接着的那一对）。按照前面将的方式旋转后，得到右边的新树。又回复了平衡。

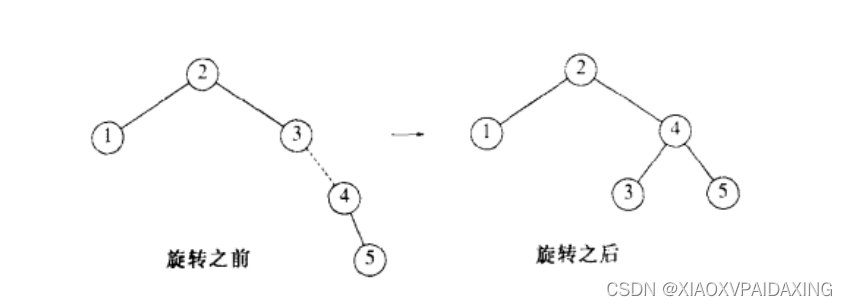
如上图所示，再接着插入4，没有出现AVL问题。但是再继续插入5的时候，如上图左边，再新插入点完往上倒可以发现3先出现了问题，右边下沉，所以把3和3的右儿子作为旋转目标（虚线连接所示）。旋转之后，如右边所示，恢复了平衡。

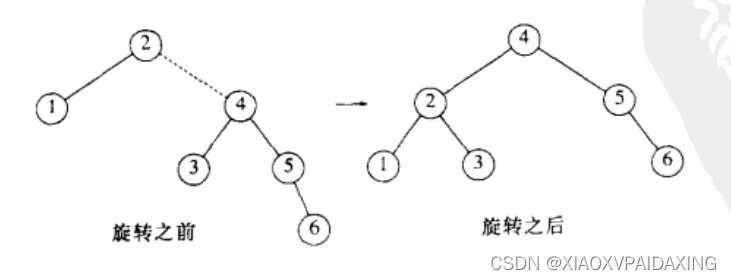
如上图所示，当再次加入6的时候，从新插入点往上倒，发现根节点2出现了错误，而且右边下层。所以把2和2的右节点4作为本次旋转的目标（如左边的虚线所示）。旋转后入右边所示，恢复AVL特性。
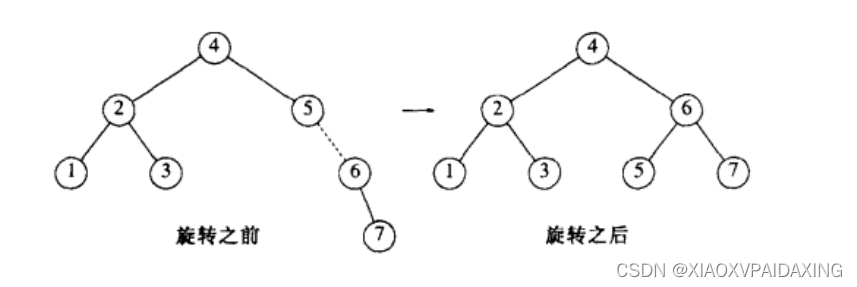如上图所示，再往树上插入7，那么首先会放在哪节点5出现不满足AVL的错误，还是右下层，所以插入后还要调整。把节点5和5的右儿子作为本次旋转目标（就是左边的虚线所示）。旋转后就成为右边所示，可见恢复成了AVL树。

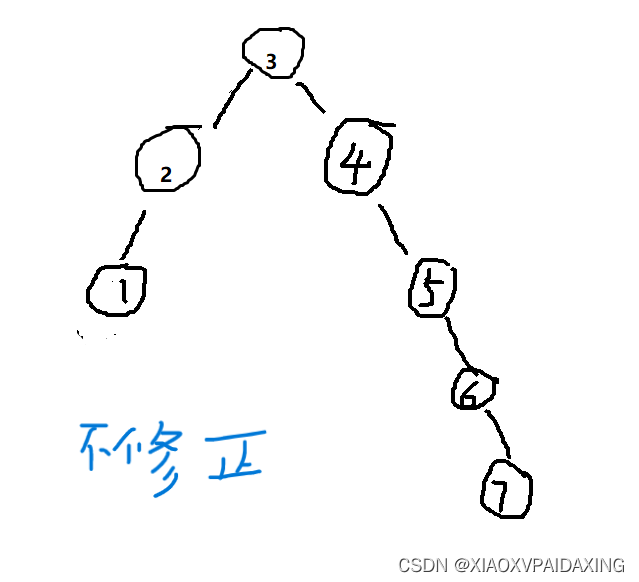
通过了上面这么多次单旋转操作，现在应该对单旋转的概念有了比较清晰的概念，它就是用来对插入后的不平衡做一次修正，保证了AVL树的完整。最后再对比一下，如果一开始就一直不用单旋转修正那么结果会咋样？如下图所示，就是每次都不修正的最终结果，这种已经不满足AVL树的定义了，对比下修正后的树，显然AVL树平均深度更小，品质更优良。

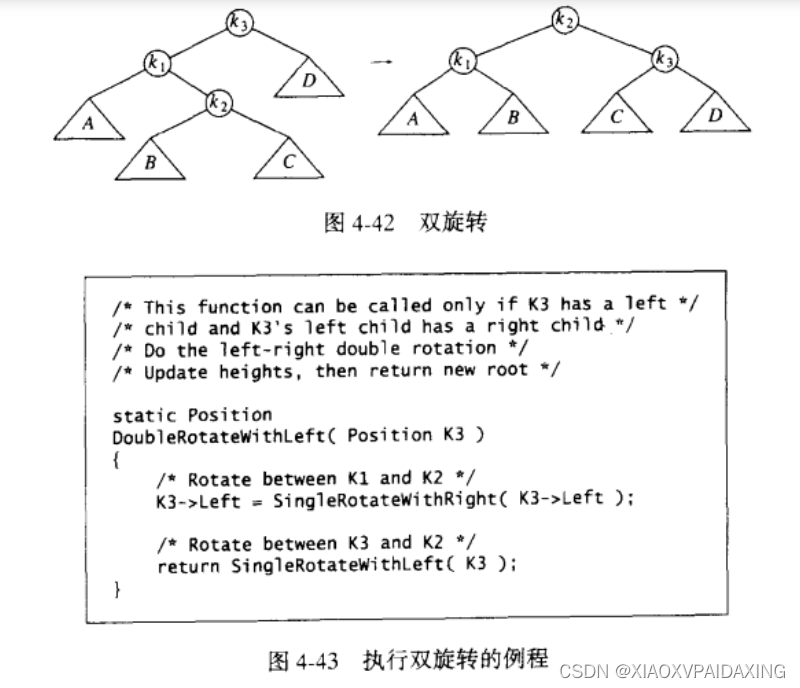
（2）双旋转
上面描述的修正算法针对的是左-左或者右-右，却对左-右或者右-左的情况行不通，为什么呢？
左-右：

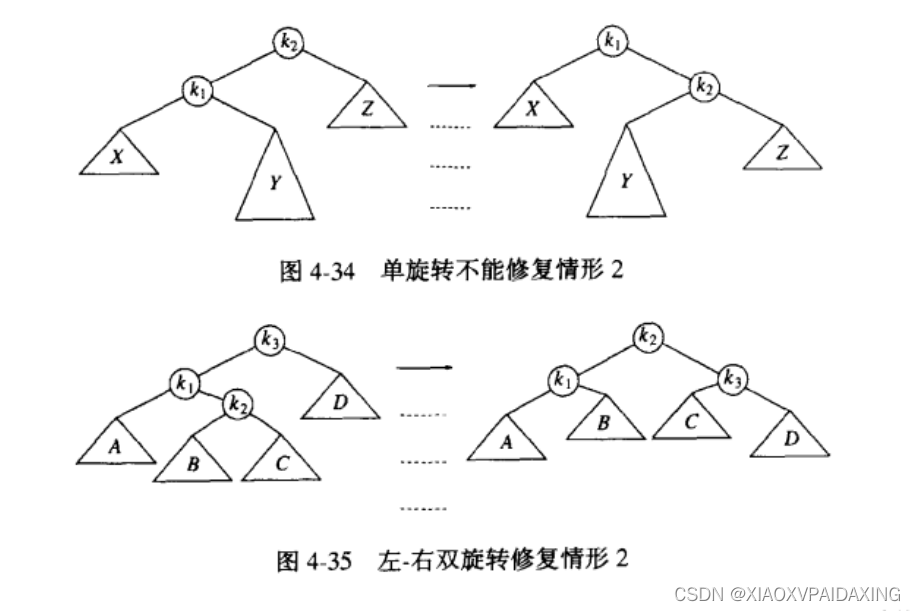
如上图所示，第一张图说的是左-右情况，如果使用前面讲的单旋转算法，那么k2出现错误，其左子树下沉，所以把k2和k1作为本次旋转对象。旋转后入右边所示，可以看到新树的根节点处还是不满足AVL，因为Y太深了。单旋转拉来拉去，只不过把Y子树放在同一层的左边或右边而已，显然不能解决问题。所以单旋转只对处在外侧的下层有效，就是左-左或者右-右。而对于处于内部的中间里的子树下层，左-右或右-左，就是无效操作了。
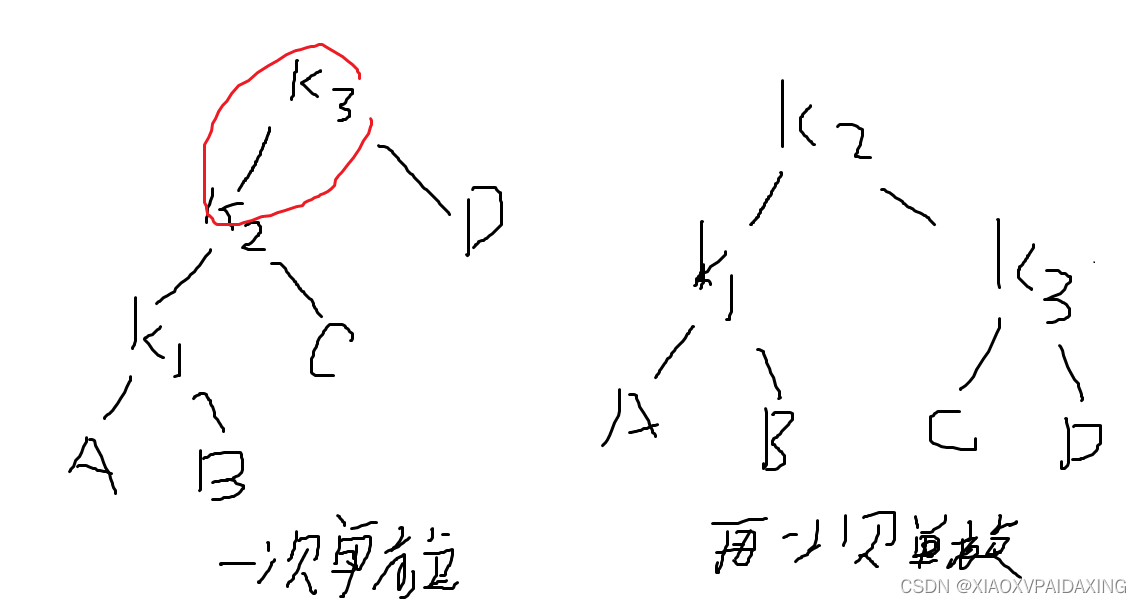
这种时候要使用双旋转，由单旋转可以看出，对第一张图，根节点k2出现了AVL错误，按照单旋转的思路就是把出错的根节点和它的子节点作为旋转对象。但通过分析可知，将它们作为旋转对象解决不了现在的问题，所以我们要使用新的旋转对象：把下图4-35的k2作为操作对象，把它往上拉到最顶端，使它成为根节点，这样Y这个模块的深度才能真正变浅。当图4-35的k2成为根节点后，因为k2大于k1小于k3，所以k1就成为新根节点的左儿子，k3就成为新根节点的右儿子，而原本k2的左右子树呢？因为旋转后，k1失去了右儿子，k3失去了左儿子，所以原本k2的左子树就移植到k1成为k1的右儿子（B小于k2大于k1），右子树就移植到k3成为k3的左儿子（C大于k2小于k3）。这就是双旋转，旋转后的新树如右边图所示，可见恢复了AVL条件。（为什么叫双旋转呢？因为一次双旋转可以拆开为两次单旋转，如上图4-35，根节点k3出错，可以先对k3->left就是k1进行单旋转，这样一来就是k2就是k3->left，然后再对k3旋转，这样一来k2->left=k3，就会得到使用一次双旋转一样的效果，直接看下图所示吧：不清楚的可以自己比划比划就明白了）

右-左：

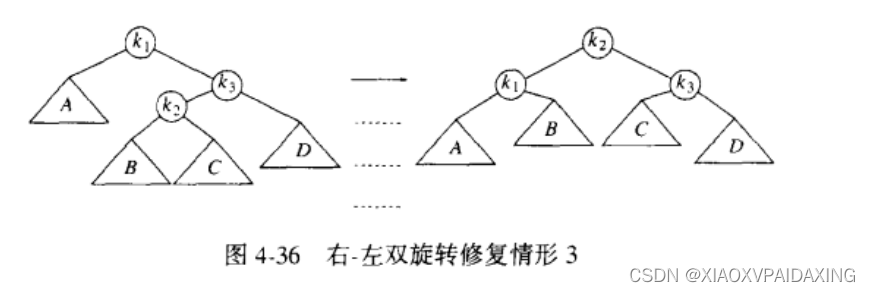
对于右-左这种情况，也一样使用双旋转，如上图所示。操作也是一样的，这里就不赘述了。

同样，对于双旋转，也举一个具体例子：

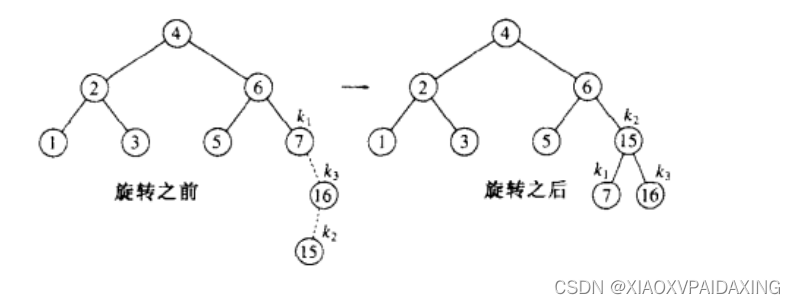
如上图所示，我们在原本的树就是1234567的树中继续先插入16，发现没问题。但再次插入15时，节点7就最先不满足AVL特性了。把节点7、16、15分别标记为k1、k3、k2，因为是右-左，所以只能使用双旋转才能解决问题，把k2往上拉，所以k1成为k2左节点，k3成为k2右节点。旋转后入右图所示。

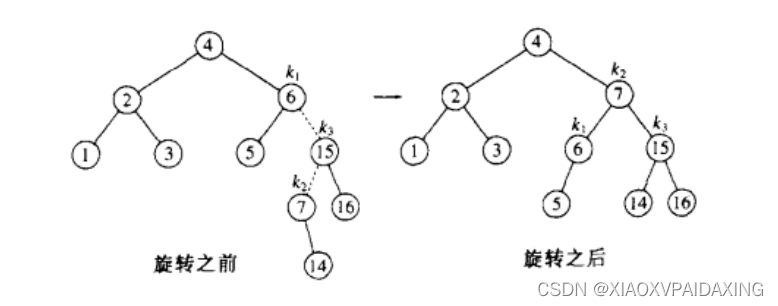
如上图所示，如果再插入14，就会如左边的树那样，最先在节点6出现AVL错误。因为是右-左情况，也只能使用双旋转才能完成修正。所以，标记6、15、7分别为k1、k3、k2，那么把k2上拉，k1成为k2的左子树，k3成为k2的右子树，然后k2原本的右子树移植到k3成为k3的左子树。如此一来就完成了旋转修正，如右边的新树所示。

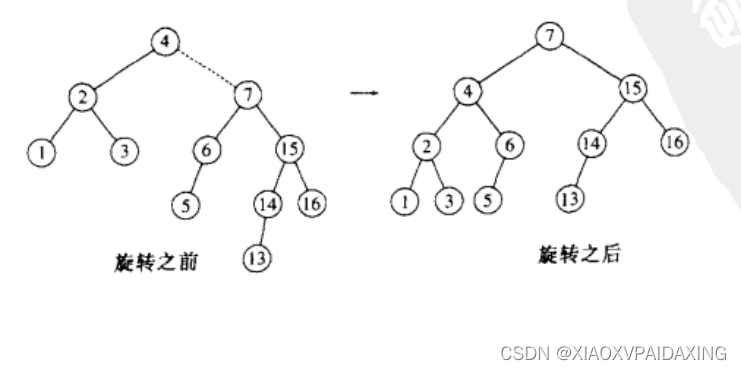
如上图所示，再插入13，那么节点4最先出现AVL错误。属于右-右情况，这时就可以使用单旋转了，把节点4和4的右儿子作为本次旋转目标，把7上拉，4自然下垂，7的左子树移植到4成为4的右子树。旋转后结果入右边的树所示，恢复了AVL条件。

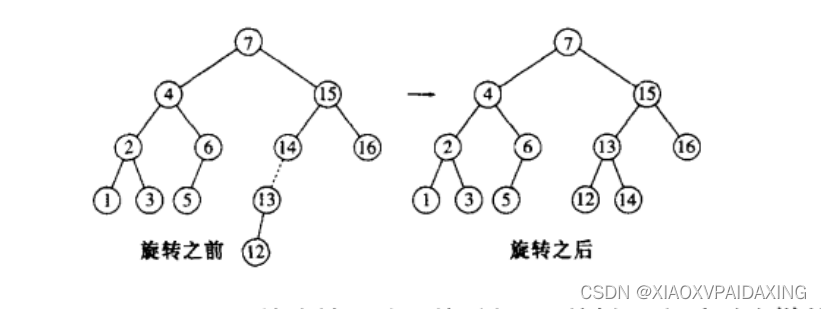
如上图所示，再继续插入12，如左边的树所示，最先在节点14出现AVL错误，是左-左情况，所以也只需使用一次单旋转即可。这里就不赘述了。
我们最后看看，如果不使用双旋转或者单选择，结果会怎样？

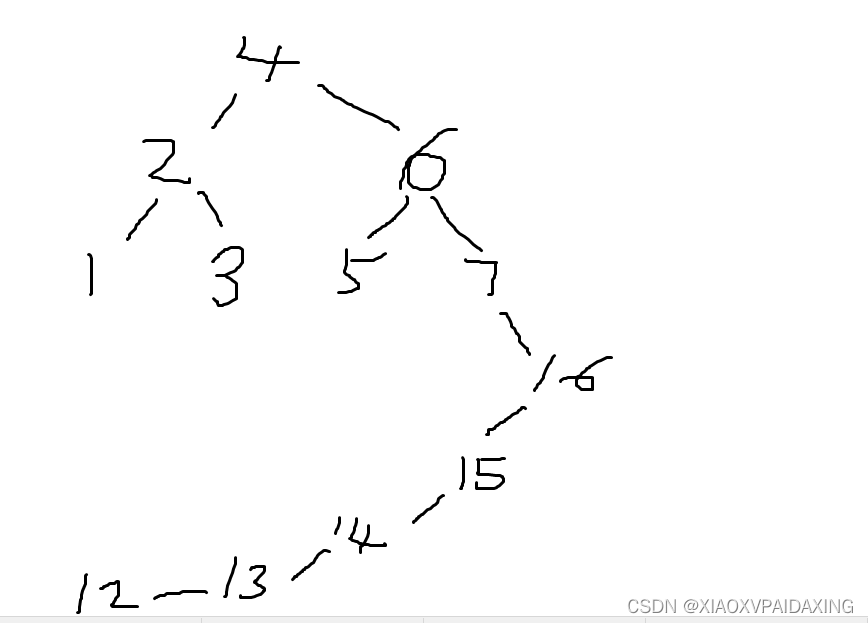
如上图所示，如果不使用双旋转或任何旋转，结果会是非常糟糕的一颗树，也不符合AVL的树定义。

（3）AVL树C编程实现
书里给了较好的编程思路示范：
声明节点只需要在二叉树的基础上增加一个高度Height即可。

到这里，关于AVL树的介绍就到这里了。

---------------------------------------------------------------更新----------------------------------------------------------------

2.4 伸展树

伸展树是一颗自调整的二叉查找树。
我们知道，二叉查找树每次操作最坏情形为O(N)，如果一个深层节点每次访问花费O(N)，那么M次访问将花费O(M*N)。也就是其实一次访问不要紧，往往一个节点被访问后，后面还会多次间断或连续要访问到这个节点，显然这种时间累积可以再进一步优化些。或者我们这样想：我们要对二叉查找树进行一系列查找，那么为了使查找时间更短，那些经常要访问的，访问频率高的节点是不是就要最好处在靠近根节点的位置上？
所以，伸展树的思路是：当一个节点被访问后，就要即可经过一系列类似AVL树使用的旋转，把它放到根上。也就是，每次查找后对树进行重构，将被查找的节点搬运到离根更近的地方。这种自调整的二叉查找树，会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

那怎么实现自调整呢？
（1）一系列单旋转
从下往上进行，要将该节点访问路径上的每一个节点都与它的父节点旋转。如下图所示，将对k1节点进行访问：其中虚线就是访问到k1的路径

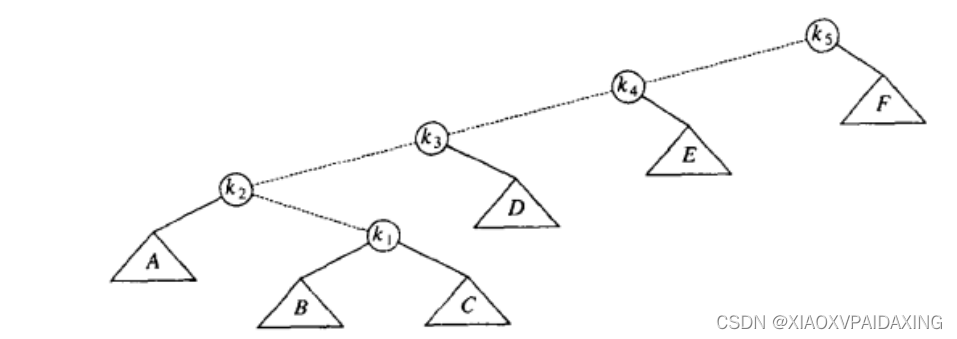
如下图所示，访问到k1后，将要对k1与其父节点k2单旋转：

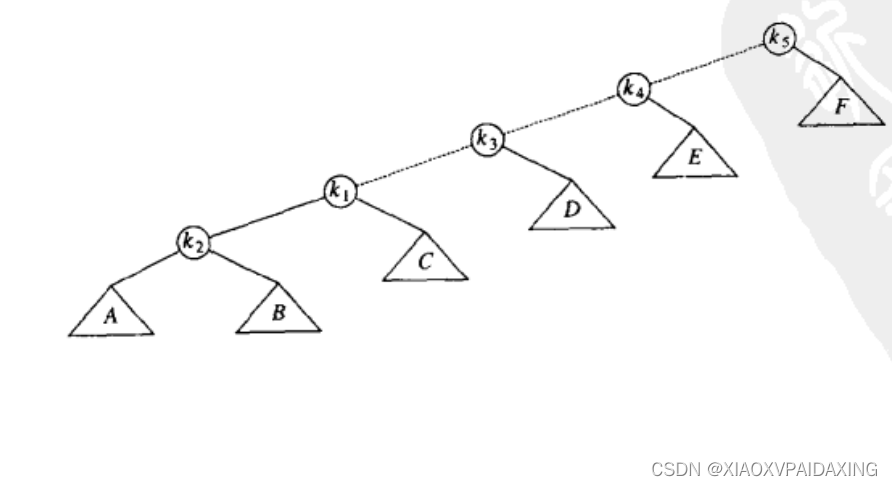
接着，还要继续讲k1与新的父节点k3进行旋转：

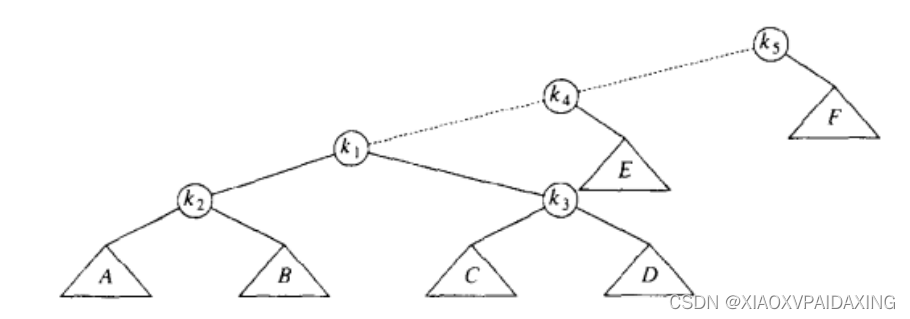
继续讲k1与k4旋转：

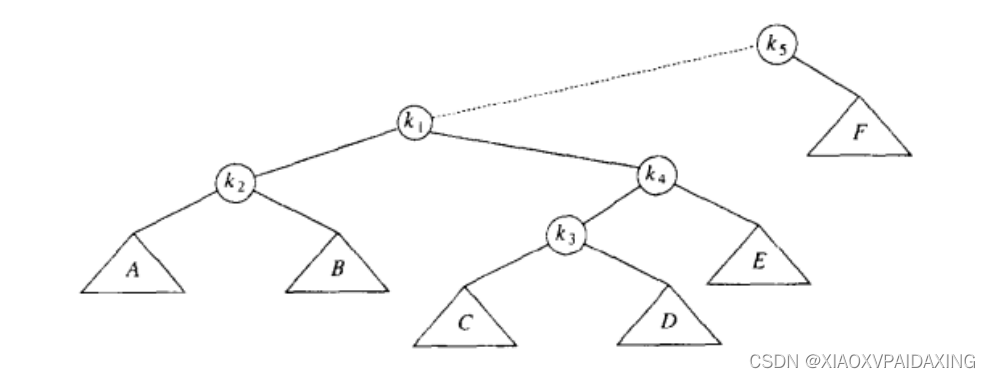
最后再把k1与k5旋转：

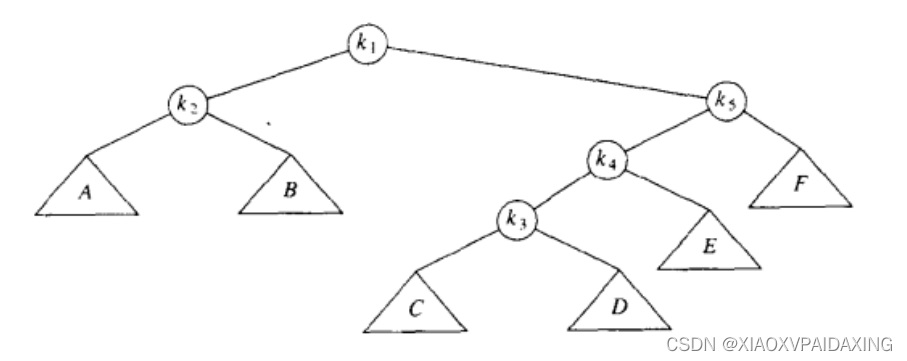
如上图所示，一个经过4次单旋转，终于把k1一步步往上推到根节点的位置。这样一来，后续如要频繁访问k1所需时间就变得很少了。

但是，也很容易想到，k1是容易了，但是它把k3挤到了深层，k1的容易是暂时的，当要访问k3时也会经过这样的一系列操作而把k3推到根节点，同样会把另一个节点挤向深处。所以虽然k1是访问时间少了，却没有明显改变原先路径上其他节点的状况。

那还有没有更好的方案呢？一种既能把目标搬运到根节点上，又能改善其他节点的深度。
比如，展开，它也是类似旋转的想法，不过有些区别：
之字型情况：zig-zag型，就是左-右或者右-左，如下图所示，这种情况使用AVL树的双旋转。

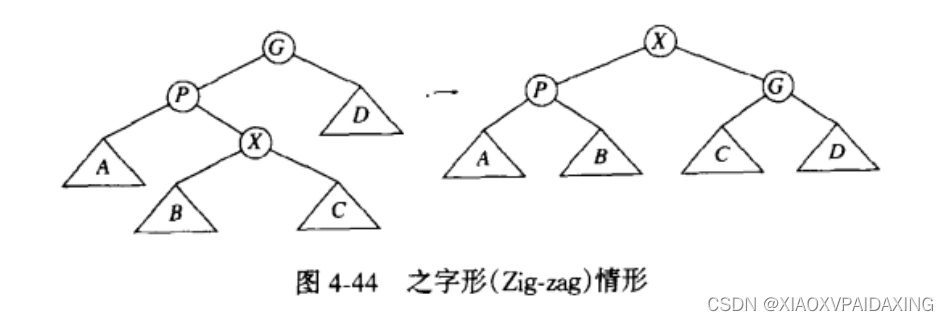
一字型：zig-zig，就是左-左或者右-右，如下图所示，这种时候就直接倒过来的方式旋转。

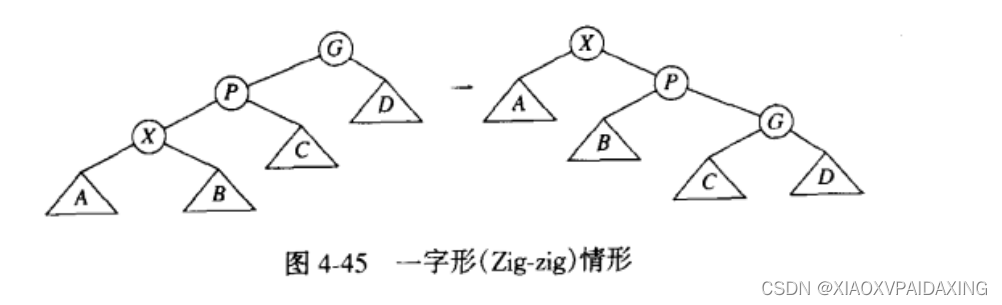
那么，展开树的旋转方式讲完了，就举个例子看看吧：如下图所示，同样，还是以这个为例子，等会儿比较一下展开方式和一系列单旋转方式的结果差异。

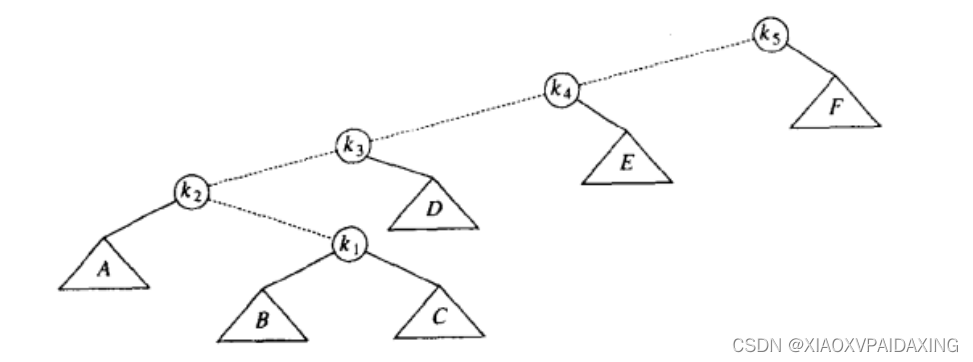
如下图所示，k1、k2、k3因为一开始是左-右结构，所以使用双旋转方式，得到下图的结果

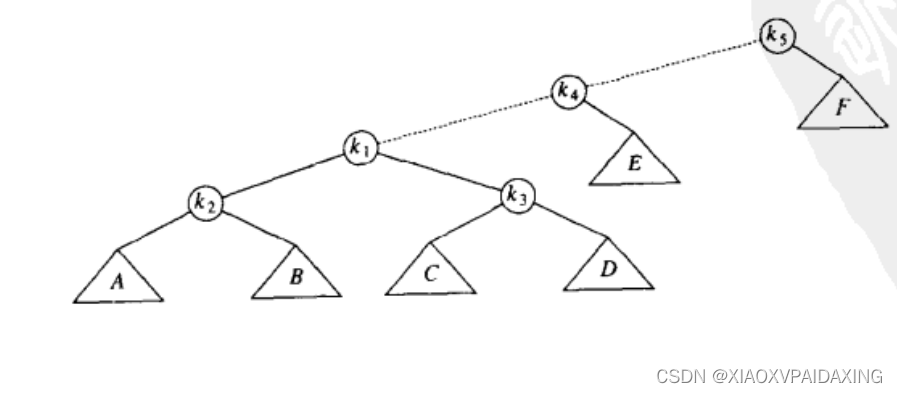
继续，如下图所示，因为前面的k1、k4、k5是左-左，所以直接倒过来旋转，结果如下图所示，到这里，使用展开方式将k1推到根节点的操作就结束了。

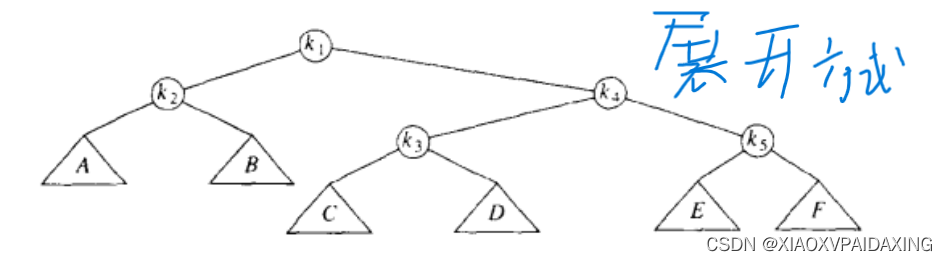
对比一下前面使用单旋转方式的结果：

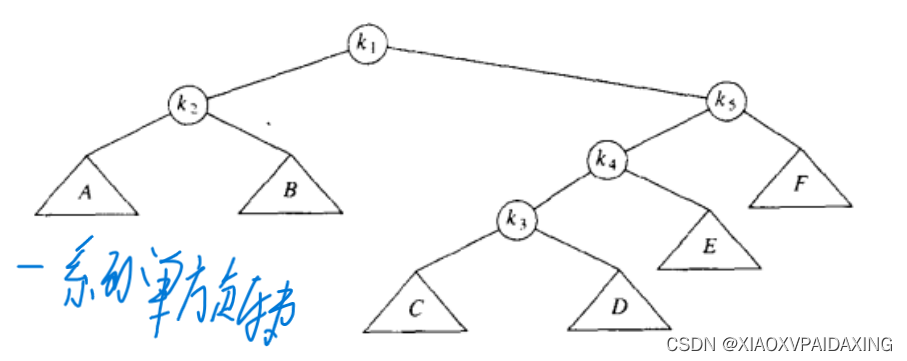
显然，同样是将k1推到根节点，但是相比于一系列单旋转方式，展开方式更加得到新树的平均深度更低，所以性能更好。也就是说，展开方式不仅可以是被查找点推近到根附近，同时还优化了原本路径上的其它节点深度，使得访问时间整体更小。

3、B-树（B Tree）

B树也主要用作查找树，不过它不是二叉树。可以说，它是一种多路搜索树，子节点数可以多个，不像二叉树那样只有两个。
B树的定义：M阶
（1）根及其儿子数在2和M之间，树叶也在2和M之间；
（2）非根非树叶的其他节点的儿子数在M/2和M之间；
（3）所有树叶都在一个深度上。

----------------------------------------------------------后续继续补充---------------------------------------------------------