能量采集 [Bzoj 2005，Noi2010]

题目地址请点击——

---

能量采集

---

【题目描述】

栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。
在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐，一共有 $n$ 列，每列有 $m$ 棵，植物的横竖间距都一样。
因此对于每一棵植物，栋栋可以用一个坐标 $(x, y)$ 来表示。
其中 $x$ 的范围是 $1$ 至 $n$，表示是在第 $x$ 列， $y$ 的范围是 $1$ 至 $m$，表示是在第 $x$ 列的第 $y$ 棵。
由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是 $(0, 0)$ 。
能量汇集机器在汇集的过程中有一定的能量损失。
如果一棵植物与能量汇集机器连接而成的线段上有 $k$ 棵植物，则能量的损失为 $2k + 1$ 。
例如，当能量汇集机器收集坐标为 $(2, 4)$ 的植物时，由于连接线段上存在一棵植物 $(1, 2)$，会产生 $3$ 的能量损失。
注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为 $1$ 。
现在要计算总的能量损失。
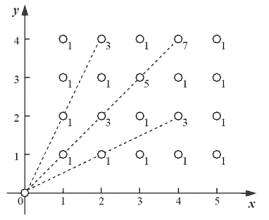
下面给出了一个能量采集的例子，其中 $n = 5$，$m = 4$，一共有 $20$ 棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。

在这个例子中，总共产生了 $36$ 的能量损失。

---

【输入描述】

仅包含一行，为两个整数 $n$ 和 $m$。

---

【输出描述】

仅包含一个整数，表示总共产生的能量损失。

---

【样例输入 1】

5 4

---

【样例输出 1】

36

---

【样例输入 2】

3 4

---

【样例输出 2】

20

---

【数据规模和约定】

对于 $10\%$ 的数据：$1 ≤ n$, $m ≤ 10$；

对于 $50\%$ 的数据：$1 ≤ n$, $m ≤ 100$；

对于 $80\%$ 的数据：$1 ≤ n$, $m ≤ 1000$；

对于 $90\%$ 的数据：$1 ≤ n$, $m ≤ 10,000$；

对于 $100\%$ 的数据：$1 ≤ n$, $m ≤ 100,000$ 。

---

【Solution】

设 $f(d)$ 为满足 $x<=n$，$y<=m$ 且 $gcd(x,y)=d$ 的个数。

根据莫比乌斯反演公式，

f(d)=∑d|iμ(id)⋅⌊ni⌋⋅⌊mi⌋

$$f(d)=\sum_{d|i}\mu(\frac{i}{d})·\lfloor\frac{n}{i}\rfloor ·\lfloor\frac{m}{i}\rfloor$$
$$\therefore ans=\sum_{i=1}^{Min(n,m)}f(i)·i$$

---

【Code】

#include <iostream>
#include <cstdio>

#define LL long long
#define Max(x,y) ((x)>(y)?(x):(y))

using namespace std;

LL n,m,ans;
bool no_prime[100010];
LL prime[100010];
int miu[100010];

int main(){

    scanf("%lld%lld",&n,&m);
    if(n>m)swap(n,m);

    miu[1]=1;
    for(LL i=2;i<=m;i++){
        if(!no_prime[i]){
            prime[++prime[0]]=i;
            miu[i]=-1; 
        }
        for(LL j=1;prime[j]*i<=m;j++){
            no_prime[prime[j]*i]=true;
            if(i%prime[j]==0){
                miu[prime[j]*i]=0;
                break;
            }
            miu[prime[j]*i]=-miu[i];
        }
    }

    for(LL i=1;i<=m;i++){
        LL tmp=0;
        while(1){
            tmp++;
            LL rk=tmp*i,sum=0;
            if(rk>n)break;
            sum+=(n/rk)*(m/rk);
            ans=ans+miu[tmp]*sum*i;
        }
    }
    printf("%lld\n",2*ans-m*n);

    return 0;
}