动态规划——0/1背包问题

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

本文主要介绍是用动态规划的方法来完成0/1背包问题，使用二维数组的常规解决办法和使用一维数组的优化。

---

一、引例

例：限定背包能够承受的质量C=5，物品数量n=4，物品质量和价值如表所示，求问题最优解。

编号	质量	价值
1	1	2
2	2	4
3	3	4
4	4	5

二、问题分析

对于动态规划问题可以分为五步走：确定dp数组以及下标含义，确定递推公式，dp数组初始化，确定遍历顺序，举例推导dp数组。

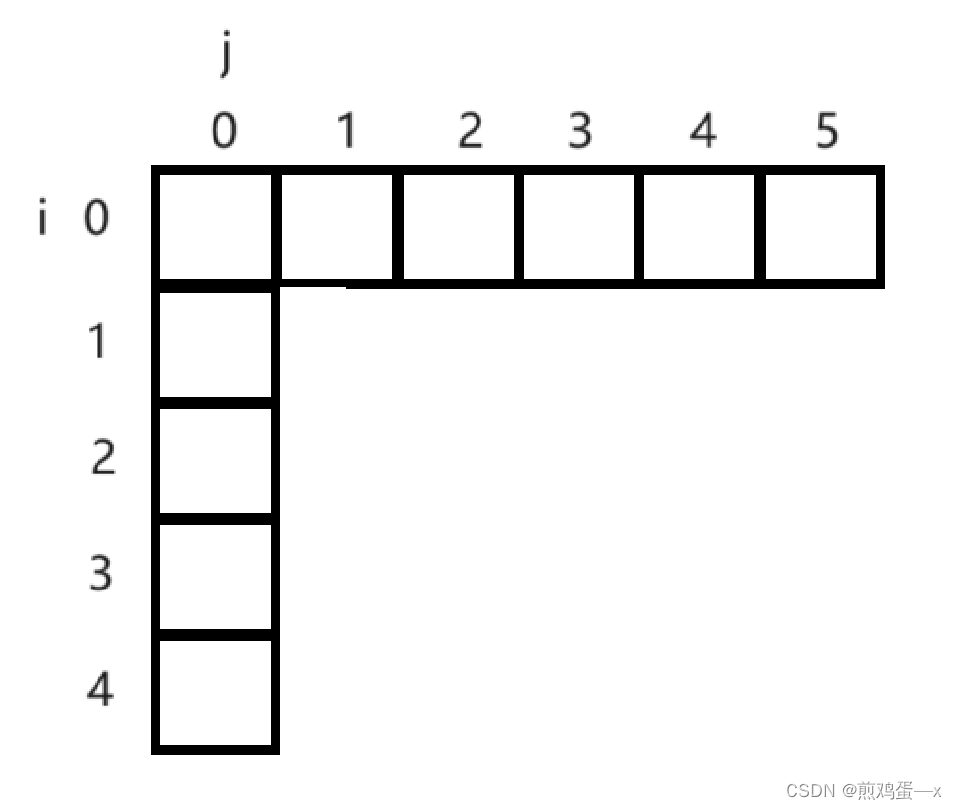
1.确定dp数组及其下标含义

设dp数组为dp[i][j], i表示物品编号，j表示背包容量，dp数组中的值表示背包内的价值。

2.确定递推公式。

情况一：选择第i个物品。
此时的背包容量为j，而前i-1个物品的决策，占用背包容量为j-w[i]，所以当前状态是由dp[i-1][j-w[i]]转换而来。

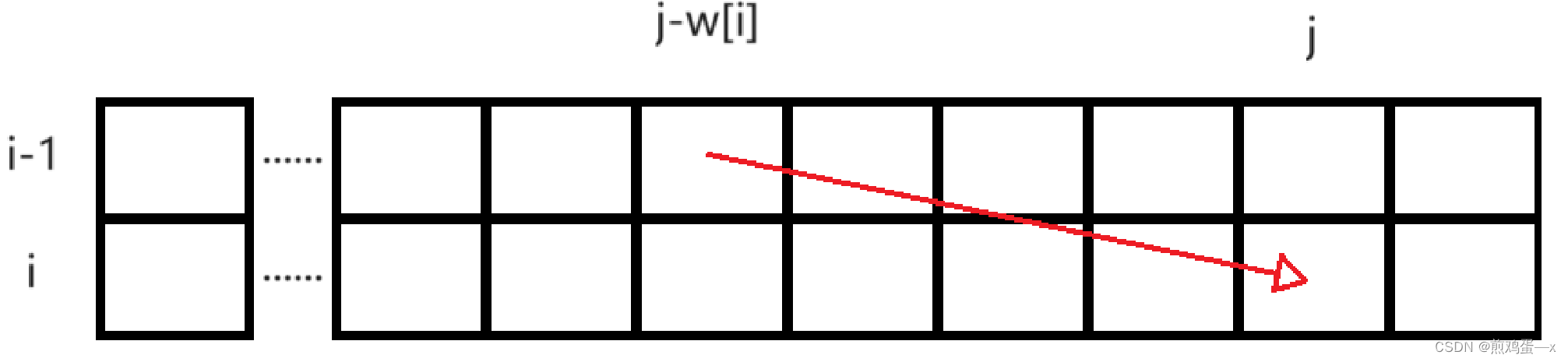
情况二：不选择第i个物品。
此时状态仍然是i-1个物品的决策成果，占用背包容量为j。

综上所述，递归方程（状态转移方程）为：

dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);

3. dp数组初始化。

如果是最大值问题，可以将所有状态初始化为最小值；如果是最小值文题，可以将所有状态初始化为最大值。

4. 确定遍历顺序

由之前的描述可以看出，该数组有两个遍历维度——物品和剩余价值。不管是先遍历物品还是剩余价值都是没问题的。至于for循环也应该是从小到大，因为dp[i][j]的状态是根据dp[i-1][j]或dp[i-1][j-w[i]]所确定的。

5. 递推过程

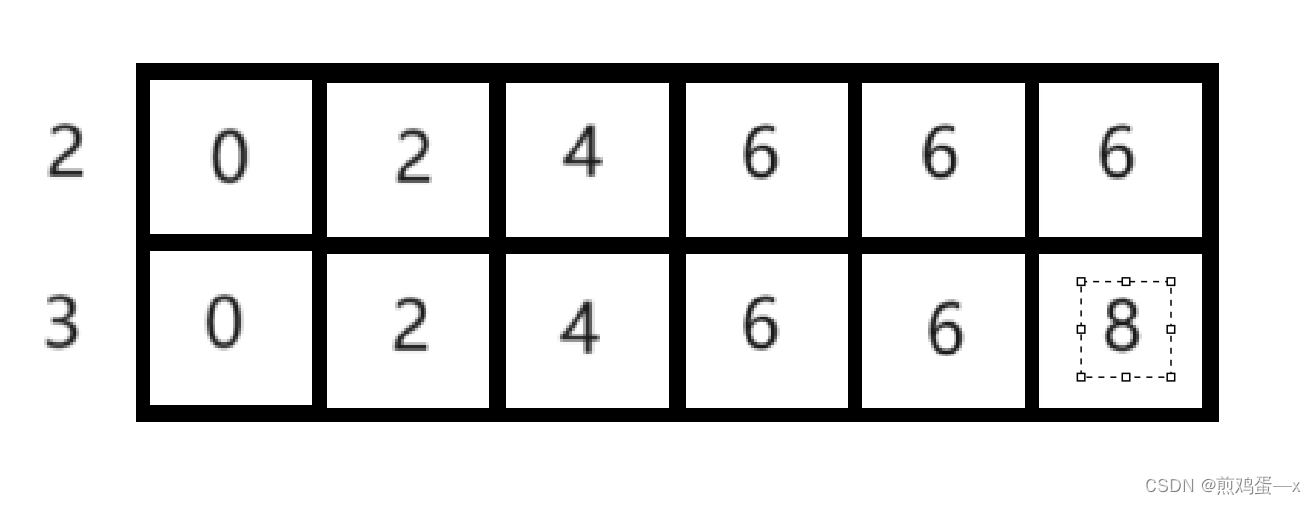
以i=3为例。

• 当j=1时，物品3的重量大于1，所以dp[3][1]=2

• 当i=2时，物品3的重量大于2，所以dp[3][2]=4

• 当i=3时，物品3重量等于3，带入递归公式，所以dp[3][3]=6

• 当j=4时，物品3重量小于4，得到dp[3][4]=6

• 当j=5时，物品3重量小于5，得到dp[3][5]=8
  

代码

```c
#include <iostream>

using namespace std;

const int maxn = 100;
int w[maxn], v[maxn], dp[maxn][maxn];
int main()
{
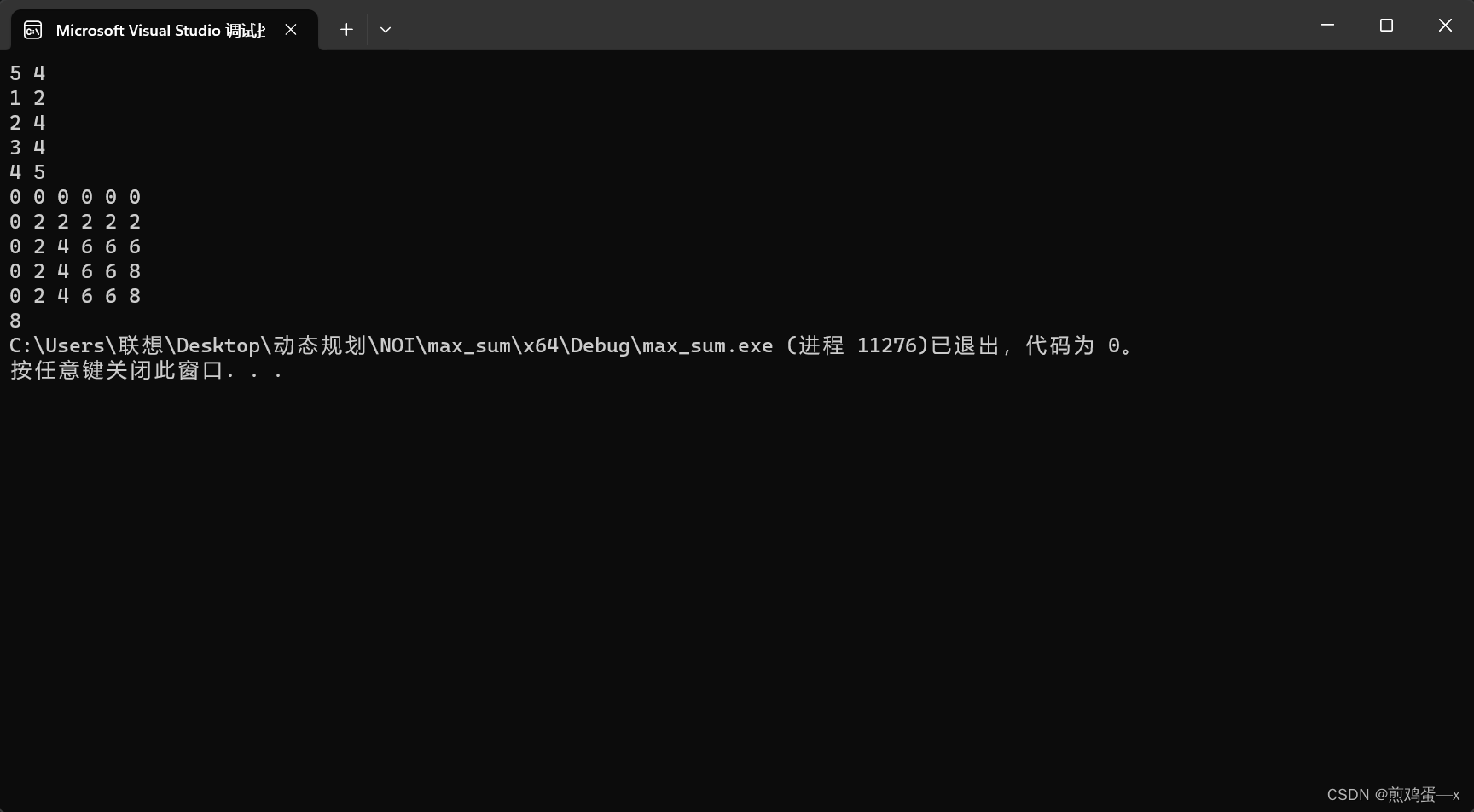
    int c, n;//背包容量，物品数量
    cin >> c >> n;
    //输入质量，价值
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> v[i];
    }
    //dp数组初始化
    for (int i = 0; i <= n; i++) dp[i][0] = 0;
    for (int j = 0; j <= c; j++) dp[0][j] = 0;
    //dp数组遍历
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= c; j++) {
            if (w[i] <= j)
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
            else
                dp[i][j] = dp[i - 1][j];

        }

    }
    //输出dp数组
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= c; j++) {
            cout << dp[i][j] << " ";
        }
        cout << endl;
    }
    cout << dp[n][c];
    return 0;
}

3. 问题优化

从上述描述来看，会发现第i行的状态只和第i-1行有关，所以我们可以将dp数组只开拓第0行，第1行。
核心代码如下：

``

for (int i = 1; i <= c; i++) {
	for (int j = 1; j <= n; j++) {
		if (j >= w[i])
			dp[i & 1][j] = max(dp[(i - 1) & 1][j], dp[(i - 1) & 1][j - w[i]] + v[i]);
		else
			dp[i & 1][j] = dp[(i - 1) & 1][j];
	}
}

``
(i & 1)实际上就是用来判断i是奇数还是偶数，因为在二进制中，奇数的最低位是1，偶数的最低位是0。所以(i & 1)的结果要么是1（奇数），要么是0（偶数）。

但是这还不是最优
在2×C维数组基础上，根据式：

dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])；

可知，dp[i][j]的计算仅与 dp[0][j] 和 dp[0][j-w[i]] 有关，如果将两行数据合并为一行数据，用dp[j]表示前 i一1 个物品、背包容量为j的子问题的最优解，则状态转移矩阵可以用下图表示。

核心代码：

        for (int j = 1; j <= c; j++) {
            if (w[i] <= j)
                dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
            else
                dp[j] = dp[j];

        }

总结

以上就是今天要讲的内容，本文仅仅简单介绍了用动态规划的方法解决0/1背包问题，及其优化。