差分 & 差分矩阵

原创已于 2025-10-30 09:48:02 修改 · 1.1k 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #算法 #线性代数 #数据结构 #c++ #c语言 #程序人生

于 2025-10-30 09:37:29 首次发布

差分

差分与前缀和是一对互逆的操作，常用于处理数组区间更新问题。差分数组能高效完成区间增减操作，而前缀和则用于还原最终结果。

题目

输入一个长度为 n 的整数序列。接下来输入 m 个操作，每个操作包含三个整数 l , r, c，表示将序列中 [l, r]之间的每个数加上c。请你输出进行完所有操作后的序列。
如果每次都遍历[l,r]，复杂度过高。我们可以构造a的差分数组b，使得a数组是b数组的前缀和。

差分数组的核心原理

给定原数组 a，其差分数组 b 定义为：

$b [1] = a [1]$
$b [i] = a [i] - a [i - 1]$ （ $i > 1$ ）
（a是b的前缀和： $a [i] = a [i - 1] + b [i]$ （ $i > 1$ ））

原数组可通过前缀和还原：
$\sum_{k=1}^{i} b[k]$

区间更新的高效实现

对原数组区间 [l, r] 增加 c，只需修改差分数组的两个位置：

$\mathrel{+}= c$
$\mathrel{-}= c$

该操作的时间复杂度为 $O (1)$ ，相比直接遍历区间 $O (n)$ 更高效。例如：

初始差分数组 b 为全零
输入 a[i] 时视为执行单点操作 insert(i, i, a[i])
执行 m 次区间操作后，通过前缀和还原结果

详细解释

示意图

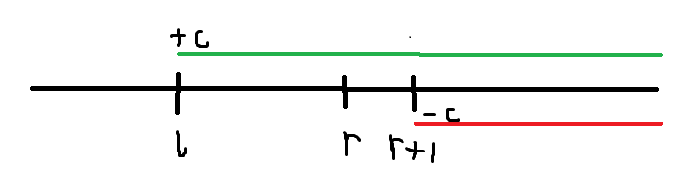
b数组如图，我们给b[l] + c，b[r + 1] - c。由于a[i] = b[1] + b[2] +...+ b[i]，b[l] + c后，得到a[l] = b[1] + b[2] +...+ (b[l] + c)，a[n] = b[1] + b[2] +...+ (b[l] + c) + ... + b[n]，所以a[l]...a[n]都加了c，但是我们要求a[l,r]之间的每个数加上 c，所以b[r + 1] - c后，得到a[r + 1] = b[1] + b[2] +...+ (b[l] + c) +... + (b[r + 1] - c)，a[n] = b[1] + b[2] +...+ (b[l] + c) + ... + (b[r + 1] - c) + ...+ b[n]，a[r + 1]...a[n]都减了c，加减抵消。
我们要构造b数组，假设a数组初始化为0，b数组也就全为0，我们在读入a数组时可以理解为对全为0的a数组进行这样的操作：在区间[1, 1]加上a[1]，在[2, 2]加上a[2]…在[n, n]加上a[n]，这样就能得到数组b。最后要输出数组a，只用求一遍前缀和就行。就不需要利用a数组来按照差分公式计算数组b了。
其实用差分公式计算数组b对时间复杂度并没有什么影响，只是巧妙地利用了一下insert函数而已。

完整代码实现

#include<iostream>
using namespace std;
const int N = 100010;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c) 
{
    b[l] += c;
    b[r + 1] -= c;
}

int main() 
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) 
    {
        scanf("%d", &a[i]);
        // 初始化差分数组，b[i] = a[i] - a[i - 1]也是可以的
        insert(i, i, a[i]); 
    }

    while(m--) 
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c); // 执行区间更新
    }

    // 计算前缀和还原结果
    for(int i = 1; i <= n; i++)
     {
        a[i] = a[i - 1] + b[i];
        printf("%d ", a[i]);
    }
	
    return 0;
}

另一种实现

也可以不需要数组a，节省空间

#include<iostream>
using namespace std;
const int N = 100010;

int n, m;
int b[N];

void insert(int l, int r, int c) 
{
    b[l] += c;
    b[r + 1] -= c;
}

int main() 
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) 
    {
    	int num;
        scanf("%d", &num);
        // 初始化差分数组，b[i] = a[i] - a[i - 1]也是可以的
        insert(i, i, num); 
    }

    while(m--) 
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c); // 执行区间更新
    }

    // 计算前缀和还原结果
    for(int i = 1; i <= n; i++) 
        printf("%d ", b[i] += b[i - 1]);
	
    return 0;
}

算法优势分析

时间复杂度优化：将 $O (mn)$ 的暴力更新降为 $O (n + m)$
空间效率：仅需额外 $O (n)$ 空间存储差分数组
通用性：适用于静态数组多次区间修改的场景

注意事项

数组下标通常从1开始以避免边界处理
差分数组初始化需通过 $n$ 次单点操作完成
最终结果需通过严格的前缀和计算获得

差分矩阵

在算法竞赛和数据处理中，经常会遇到需要对矩阵的子矩阵进行批量增减操作的情况。如果直接遍历子矩阵的每个元素进行修改，时间复杂度会很高 $O (q nm)$ 。差分矩阵技术能将时间复杂度优化到 $O (nm + q)$ ，显著提升效率。

题目

输入一个 n行 m列的整数矩阵，再输入 q个操作，每个操作包含五个整数 x1 ,y1 ,x2 ,y2 ,c，其中 (x1,y1)和 (x2,y2)表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上 c。请你将进行完所有操作后的矩阵输出。
如果每次都遍历[x1, y1]，[x2, y2]，复杂度过高。我们可以构造a的差分数组b，使得a数组是b数组的前缀和。

差分矩阵的核心思想

差分矩阵基于前缀和与差分的概念。对于原矩阵a，构造其差分矩阵b，使得a[i][j]等于b矩阵从(1,1)到(i,j)的前缀和。通过维护差分矩阵b，可以高效实现区域增减操作。

对子矩阵(x1,y1)-(x2,y2)增加c的操作，转化为对差分矩阵b的四个关键位置修改：

b[x1][y1] += c
b[x2+1][y1] -= c
b[x1][y2+1] -= c
b[x2+1][y2+1] += c

这种四角修改法确保只有目标子矩阵内的元素会正确增加c值。
示意图

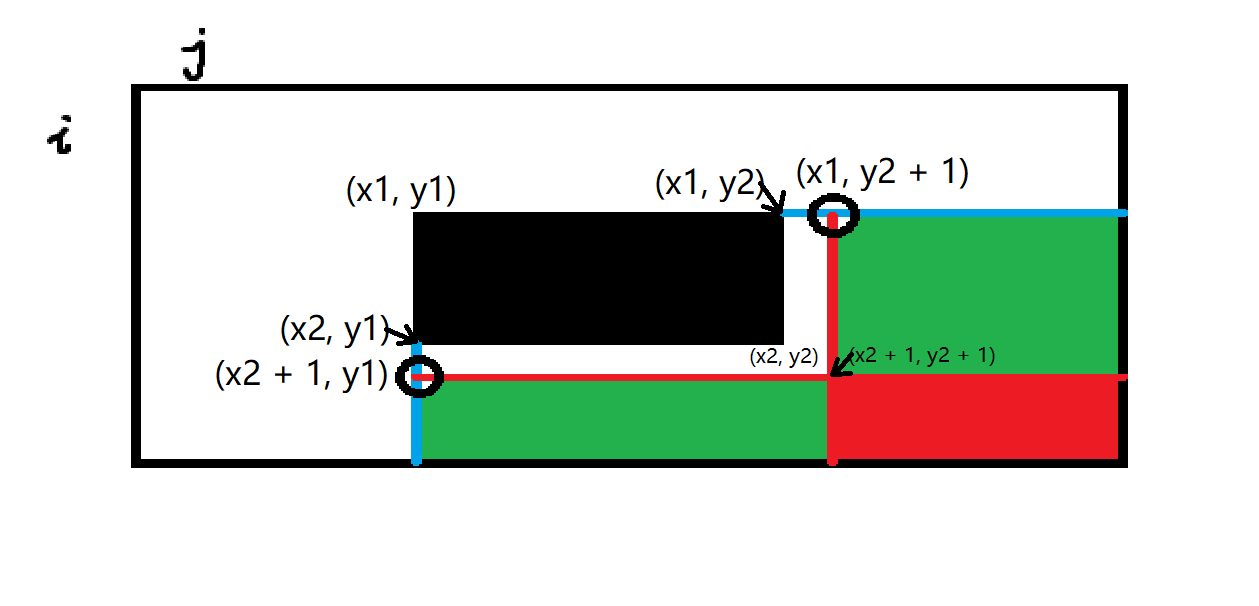
b数组如图，我们给b[x1, y1] + c，b[x1, y2 + 1] - c，b[x2 + 1, y1] - c，b[x2 + 1, y2 + 1] + c。由于a[i]是前缀和，b[x1, y1] + c后，蓝色边框区域在求前缀和时都会加c，但是我们要求黑色区域的每个数加上 c，所以b[x1, y2 + 1] - c，b[x2 + 1, y1] - c后，两块红色边框区域都减了c，绿色区域被减了一次，但是红色区域被减了两次，b[x2 + 1, y2 + 1] + c后，加减抵消。
我们要构造b数组，假设a数组初始化为0，我们在读入a数组时可以理解为在(i，j)，(i，j)这个区域加上a[i，j]，这样就能得到数组b。最后要输出数组a，只用求一遍前缀和就行。

实现步骤

初始化差分矩阵时，可以将每个元素的初始值视为在单点(i,j)到(i,j)的子矩阵上增加a[i][j]的操作：

void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c; 
    b[x2+1][y2+1] += c;
}

// 初始化差分矩阵
for(int i = 1; i <= n; i++) {
    for(int j = 1; j <= m; j++) {
        insert(i, j, i, j, a[i][j]);
    }
}

处理完所有操作后，通过二维前缀和计算恢复最终矩阵：

for(int i = 1; i <= n; i++) {
    for(int j = 1; j <= m; j++) {
        a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
    }
}

二维前缀和大家可以去看看我的这篇文章 -> 任意门

复杂度分析

构造初始差分矩阵： $O (nm)$
处理q次操作： $O (q)$
计算最终矩阵： $O (nm)$
总时间复杂度： $O (nm + q)$

相比直接暴力修改的 $O (q nm)$ 时间复杂度，差分矩阵在q较大时有显著优势。

应用场景

这种技术适用于：

大规模矩阵区域修改
离线处理批量更新
需要多次查询最终结果的场景

特别在图像处理、数值模拟、游戏开发等领域有广泛应用。

代码实现示例

完整实现参考以下代码框架：

#include <iostream>
using namespace std;

const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    
    // 初始化差分矩阵
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]), insert(i,j,i,j,a[i][j]);
    
    // 处理操作
    while(q--) {
        int x1,y1,x2,y2,c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1,y1,x2,y2,c);
    }
    
    // 计算最终矩阵
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
        	//一边计算，一边打印
            a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
            printf("%d ", a[i][j]);
        }
        printf("\n");
    }
    
    return 0;
}

扩展思考

差分矩阵思想可以推广到更高维度，如三维空间的立方体区域修改。核心仍是正确设置差分边界点的增减操作，使修改只影响目标区域。
掌握差分技巧不仅能提升算法效率，也能培养对数据结构的深刻理解。在实际应用中，结合具体问题灵活运用差分思想，往往能创造出更优的解决方案。

算法内容来自AcWing算法基础课，感谢AcWing老师的详细讲解。