并查集之合并集合

最新推荐文章于 2025-11-07 17:12:13 发布

原创最新推荐文章于 2025-11-07 17:12:13 发布 · 772 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #c++ #c语言 #学习方法 #面试 #程序人生

并查集：高效合并与查询集合

并查集（Disjoint Set Union, DSU）是一种用于高效管理集合的数据结构，支持两种核心操作：合并两个集合和查询元素是否属于同一集合。它在图论、连通性问题中广泛应用，时间复杂度接近常数级。本文将详细介绍并查集的原理、实现及一个典型问题：合并集合。

问题描述

给定 $n$ 个元素（编号 $\sim n$ ），初始时每个元素独立构成一个集合。需要处理 $m$ 个操作：

M a b：合并元素 $a$ 和 $b$ 所在集合（若已同集，则忽略）。
Q a b：查询 $a$ 和 $b$ 是否在同一集合中，输出 Yes 或 No。

输入格式：首行为 $n$ 和 $m$ ，随后 $m$ 行每行一条指令。
输出格式：对每个查询指令输出结果。

并查集原理

并查集的核心思想是用树结构表示集合：

每个集合以一棵树表示，根节点的编号即集合编号。
每个节点存储其父节点指针 $p [x]$ ，初始时 $p [x] = x$ （自身为根）。
查询操作：通过父指针递归找到根节点，判断元素所属集合。
合并操作：将一棵树的根节点指向另一棵树的根节点。

优化技术路径压缩在查询时将路径上的节点直接指向根节点，使后续查询接近 $O (1)$ 时间复杂度。

操作详解

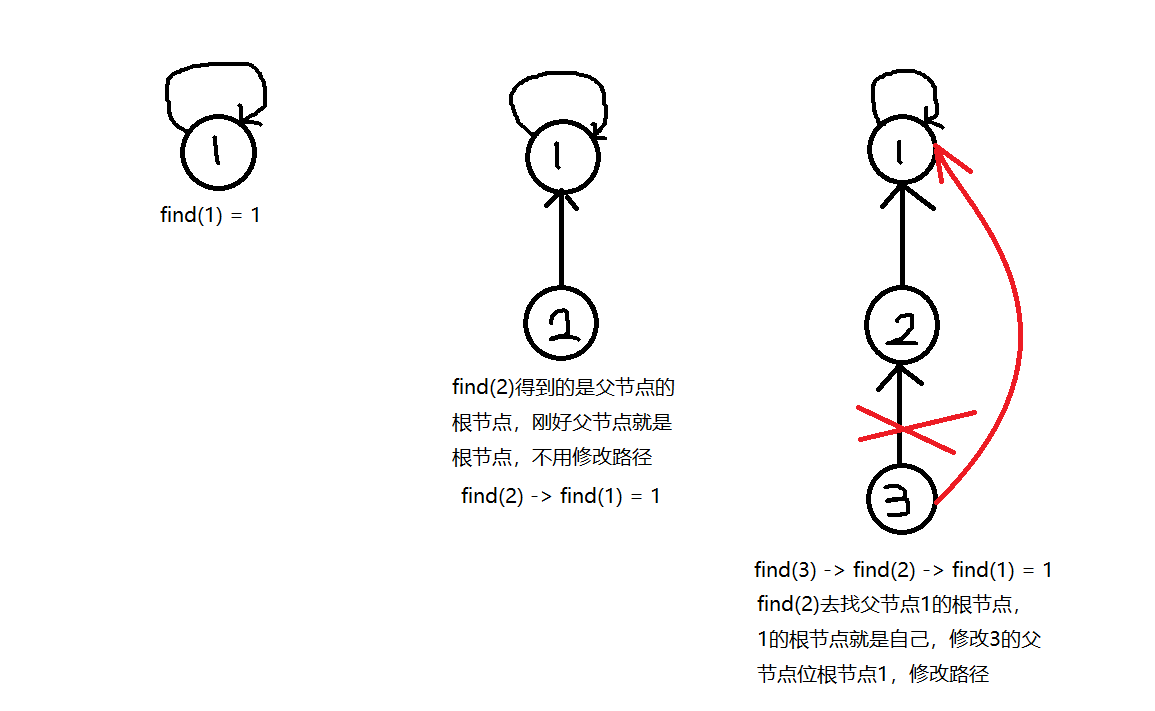
查询（Find）
递归找到元素 $x$ 的根节点，并压缩路径：
- 若 $\neq x$ ，则令 $\text{find}(p[x])$ ，直接指向根节点。
- 返回根节点 $p [x]$ 。
合并（Union）
找到 $a$ 和 $b$ 的根节点 $root_a$ 和 $root_b$ ，令 $p[root_a] = root_b$ （将 $a$ 所在集合挂到 $b$ 所在集合下）。
查询是否同集
比较 $find(a)\text{find}(a)$ 和 $find(b)\text{find}(b)$ ：若相等，则在同一集合。

路径压缩优化

路径压缩是并查集高效的关键：

在 find 函数中，递归将节点的父指针指向根节点。
效果：树高度降低，后续操作时间复杂度降至接近 $O (1)$ 。
数学上，均摊时间复杂度为 $O(α(n))O(\alpha(n))$ ，其中 $α\alpha$ 是反阿克曼函数（极小值）。

find函数示意图

代码实现

以下是基于C++的高效实现，包含路径压缩：

#include <iostream>
using namespace std;

const int N = 1e5 + 10; // 最大元素数
int p[N]; // 父节点数组
int n, m; // 元素数和操作数

// 查找函数，一边找集合的根节点，一边把自己的父节点修改为集合的根节点
int find(int x) 
{
    if (p[x] != x) p[x] = find(p[x]); // 递归压缩路径
    return p[x]; // 返回根节点
}

int main() 
{
    scanf("%d%d", &n, &m);
    // 初始化：每个元素为独立集合
    for (int i = 1; i <= n; i++) p[i] = i;

    char op[2]; // 用字符串避免空格问题
    int a, b;
    while (m--) 
    {
        scanf("%s%d%d", op, &a, &b);
        if (op[0] == 'M') 
        {
            // 合并：让a的根节点指向b的根节点
            p[find(a)] = find(b);
        } 
        else if (op[0] == 'Q') 
        {
            // 查询：比较根节点
            if (find(a) == find(b)) printf("Yes\n");
            else printf("No\n");
        }
    }
    return 0;
}

代码解释：

初始化：循环设置 $p [i] = i$ ，使每个元素初始为根节点。
读取数据：scanf(“%s”, op) 会忽略输入开始前的任何空格（例如，如果输入以空格开头，它会跳过这些空格）。然后，它开始读取字符并将其存储到op数组中。当遇到空格、制表符或换行符时，%s会停止读取，并将当前字符视为字符串的结尾（自动添加空字符\0）。
find函数：递归压缩路径，确保后续查询高效。
合并操作：p[find(a)] = find(b) 将 $a$ 所在集合合并到 $b$ 所在集合。
查询操作：直接比较根节点是否相同。