一个数组中找出连续子向量的最大和 分治算法 扫描算法O(n)

算法设计艺术

输入具有n个整数的向量data,输出向量的任意连续子向量的最大和,
当所有输入都是负数时,综合的最大子向量是空向量,总和为0;
例如输入10个数
31,-41,59,26,-53,58,97,-93,-23,84

输出
data[2..6]的和 187
59+26+(-53)+58+97

其中最高效的是扫描算法O(n)
分治算法O(n*logn)
基本算法是O(n^2)

/*
description:
从一个数组中找出连续子向量的最大和

参考<<编程珠玑>>
author:Jason
date:20160515
*/
#include<stdio.h>
#include<iostream>
using namespace std;

//最简单的方法  复杂度 O(n^3)
int maxsum_fun1(int data[],int len)
{
    int maxsofar=0;
    int sum=0;

    for(int i=0;i<len;i++)
    {
        for (int j=i;j<len;j++)
        {
            sum=0;
            for (int k=i;k<j;k++)
            {
                sum+=data[k];
            }
            maxsofar=max(maxsofar,sum);
        }
    }
    return maxsofar;

}

//复杂度 O(n^2)
int  maxsum_fun2(int data[],int len)
{
    int maxsofar=0;
    int sum=0;

    for(int i=0;i<len;i++)
    {
        sum=0;
        for (int j=i;j<len;j++)
        {
            sum+=data[j];
            maxsofar=max(maxsofar,sum);
        }
    }

    return maxsofar;
}

//分治算法  O(n*logn)
int maxsum_fun3(int data[],int l,int u)
{
    int sum=0;
    if (l>u) 
    {
        return 0;
    }
    if (l==u)
    {
        return max(0,data[l]);
    }

    //find max crossing left
    int m=(l+u)/2;
    int lmax=0;
    sum=0;
    for (int i=m;i>=l;i--)
    {
        sum+=data[i];
        lmax=max(lmax,sum);
    }

    //find max crossing right
    int rmax=0;
    sum=0;
    for(int i=(m+1);i<=u;i++)
    {
        sum+=data[i];
        rmax=max(rmax,sum);
    }

    int max_medium=rmax+lmax;
    int max_left=maxsum_fun3(data,l,m);
    int max_right=maxsum_fun3(data,m+1,u);
    //chose one max  
    int max_result=max(max_medium,max_left);
    max_result=max(max_result,max_right);
    return max_result;
}
//扫描算法 O(n)
int maxsum_fun4(int data[],int len)
{
    int maxsofar=0;
    int maxending=0;
    for (int i=0;i<len;i++)
    {
        maxending=max(maxending+data[i],0);
        maxsofar=max(maxending,maxsofar);
    }
    return maxsofar;
}
int main()
{
    int data[]={31,-41,59,26,-53,58,97,-93,-23,84};
    int len=10;
    cout<<"data:"<<endl;
    for(int i=0;i<len;i++)
    {
        cout<<data[i]<<" ";
    }
    cout<<endl;

    cout<<"--------------------------------"<<endl;
    int max_result_1=   maxsum_fun1(data,len);
    cout<<"fun1  O(n^3)  \nmax_result_1:"<<max_result_1<<endl;


    cout<<"--------------------------------"<<endl;
    int max_result_2=maxsum_fun2(data,len);
    cout<<"fun2  O(n^2)  \nmax_result_2:"<<max_result_2<<endl;
    cout<<"--------------------------------"<<endl;
    int max_result_3=maxsum_fun3(data,0,len-1);
    cout<<"fun3  O(n*logn)  \nmax_result_3:"<<max_result_3<<endl;
    cout<<"--------------------------------"<<endl;
    int max_result_4=maxsum_fun4(data,len);
    cout<<"fun4  O(n)  \nmax_result_4:"<<max_result_4<<endl;
    return 0;

}

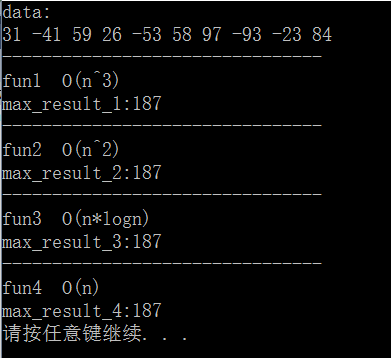
结果如下: