HDU1252-Hike on a Graph

Hike on a Graph

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 215    Accepted Submission(s): 101

Problem Description

"Hike on a Graph" is a game that is played on a board on which an undirected graph is drawn. The graph is complete and has all loops, i.e. for any two locations there is exactly one arrow between them. The arrows are coloured. There are three players, and each of them has a piece. At the beginning of the game, the three pieces are in fixed locations on the graph. In turn, the players may do a move. A move consists of moving one's own piece along an arrow to a new location on the board. The following constraint is imposed on this: the piece may only be moved along arrows of the same colour as the arrow between the two opponents' pieces.

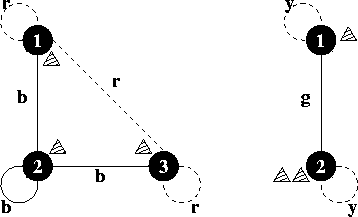
In the sixties ("make love not war") a one-person variant of the game emerged. In this variant one person moves all the three pieces, not necessarily one after the other, but of course only one at a time. Goal of this game is to get all pieces onto the same location, using as few moves as possible. Find out the smallest number of moves that is necessary to get all three pieces onto the same location, for a given board layout and starting positions.

 

Input

The input file contains several test cases. Each test case starts with the number n. Input is terminated by n=0. Otherwise, 1<=n<=50. Then follow three integers p1, p2, p3 with 1<=pi<=n denoting the starting locations of the game pieces. The colours of the arrows are given next as a m×m matrix of whitespace-separated lower-case letters. The element mij denotes the colour of the arrow between the locations i and j. Since the graph is undirected, you can assume the matrix to be symmetrical.

 

Output

For each test case output on a single line the minimum number of moves required to get all three pieces onto the same location, or the word "impossible" if that is not possible for the given board and starting locations.

 

Sample Input

   
   

    
    3 1 2 3  
   
   
   
   

    
    r b r  
   
   
   
   

    
    b b b 
   
   
   
   

    
     r b r  
   
   
   
   

    
    2 1 2 2 
   
   
   
   

    
     
    
    y g  
   
   
   
   

    
    g y  
   
   
   
   

    
    0
   
   
   
   

    
     
   
   
   
   

    
    题意：题目说的是有一个无相完全图，每条边都有一种颜色，有三个玩家分别在三个位置，然后他们开始从自己的位置移动，每次只能移动一步，移动的规则是当且仅当沿着移动的那条边和另外两个玩家之间的边的颜色相同。比如有三个玩家ABC，如果A想要移动到i则必须满足A到i的边的颜色和B,C z之间边的颜色相同，否则不能移动！问最少几步能将三个棋子移动到同一点上面。
   
   
   
   

    
     
   
   
   
   

    
    思路：广度优先搜索，用一个vis[N][N][N]存放从三个玩家的初始状态到目前状态走了多少步，队列存放的是三个玩家位置状态！
   
   
   
   

    
     
   
   
   
   

    
    代码：
   
   
   
   

    
    

     
     

      
      #include<cstdio>
#include<queue>
#include<string.h>
using namespace std;
struct node
{
    int x,y,z;
};
int vis[52][52][52],n;
char map[52][52]; 
int bfs(struct node start)
{
    queue<struct node>q;
    memset(vis,0,sizeof(vis));
    q.push(start);
    vis[start.x][start.y][start.z]=1;//注意，如果是在每次出队时检验是否成功，则必须初始化起点为1 
    while(!q.empty())
    {
        struct node tmp=q.front();
        q.pop();
        if(tmp.x==tmp.y&&tmp.y==tmp.z)//三点重合，说明已经移动到同一点，符合题意 
            return vis[tmp.x][tmp.y][tmp.z]-1;
        for(int i=1;i<=n;i++)
        {
            if(vis[i][tmp.y][tmp.z]==0&&map[tmp.x][i]==map[tmp.y][tmp.z])//x可以移动到i点，且这种状态为出现过
            {
                vis[i][tmp.y][tmp.z]=vis[tmp.x][tmp.y][tmp.z]+1;
                struct node cur=tmp;
                cur.x=i;
                q.push(cur);
            }
            if(vis[tmp.x][i][tmp.z]==0&&map[tmp.y][i]==map[tmp.x][tmp.z])//y可以移动到i点，且这种状态为出现过
            {
                vis[tmp.x][i][tmp.z]=vis[tmp.x][tmp.y][tmp.z]+1;
                struct node cur=tmp;
                cur.y=i;
                q.push(cur);
            }
            if(vis[tmp.x][tmp.y][i]==0&&map[tmp.z][i]==map[tmp.x][tmp.y])//z可以移动到i点，且这种状态为出现过
            {
                vis[tmp.x][tmp.y][i]=vis[tmp.x][tmp.y][tmp.z]+1;
                struct node cur=tmp;
                cur.z=i;
                q.push(cur);
            }
        }
    }
    return -1;//表示未能到达 
}
int main()
{
    int i,j,r;
    struct node start;
    while(scanf("%d",&n),n)
    {
        scanf("%d %d %d",&start.x,&start.y,&start.z);
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                scanf(" %c",&map[i][j]);
        r=bfs(start);
        if(r!=-1) printf("%d\n",r);
        else printf("impossible\n");  
    }
    return 0;
}