8 CELP编码介绍
Speex基于CELP,即码激励线性预测(Code Excited Linear Prediction)。本章介绍CELP基本原理,所以如果你已经对CELP很熟悉,可以跳到第9章。CELP技术基于以下3点思想:
1)利用一个线性预测(LP)模型模拟声道
2)使用(自适应的和固定的)密码本条目作为LP模型的输入(激励)
3)在“感知加权域”执行闭合搜索
本章介绍CELP的基本思想,其原理也在不断发展中。
8.1 语音产生的声源滤波器模型
产生语音的声源滤波器模型假设声带是声音的起源(激励信号),并且声道作为一个滤波器对各种语音声音调整谱形状。虽然这只是一个近似,却因为其简单性使得这一模型广泛用于语音编码中。这一模型也是为什么大多数语音编解码器(包括Speex)对音乐信号效果很差的原因。在这一模型中,不同的因素能根据激励(源)和谱形(滤波器)得以区分。浊音(如元音)是一个周期性激励信号,并能用一个时域脉冲序列近似或频域固定间隔的谐波近似。另一方面,摩擦声(如“s”,“sh"和”f“)是一种类似于高斯白噪声的激励信号,所谓的浊音摩擦音(如”z“和”v“)是一个由谐波部分和噪声部分组成的激励信号。
声源滤波器模型通常结合线性预测使用。CELP模型基于声源滤波器模型,如图8.1中CELP解码器所示。
图8.1 语音合成(解码)的CELP模型
8.2 线性预测(LPC)
线性预测是包括CELP在内的许多语音编码技术的基础,其思想是用x[n]之前的N个样本的线性组合来预测x[n]:
其中y[n]就是x[n]的线性预测。预测误差为:
线性预测的目的就是寻找使得误差平方和函数最小的最优预测系数ai:
可通过对ai求导,并使其等于0求得:
对于一个N阶滤波器,滤波器系数ai通过求解一个N*N线性系统Ra=r求得,其中
R(m)为信号x[n]的自相关:
因为R是Hermitian Toeplitz矩阵,所以可以利用Levinson-Durbin算法,使得复杂度由O(N^3)降低为O(N^2)。而且,可以证明A(z)的所有根都在单位圆内,这意味着1/A(z)总是稳定的。实际应用中由于精确度有限,有两个常用技术可以保证滤波器稳定:第一,将R(0)乘以一个比1稍微大一点的数(如1.0001),等价于对信号添加噪声;第二,也可以对自相关加窗,等价于在频域滤波,减少尖锐的共振。
8.3 音高预测
在浊音段,语音信号是周期的,所以可以通过对过去激励乘以一个增益来近似当前激励信号e[n]:
其中T为音高周期,B为音高增益。我们称其为长期预测,因为激励是由e[n-T]预测而来,而T>>N。
8.4 创新码本
最后的激励e[n]是预测音高来自固定码本信号c[n]之和,即码激励线性预测编码。最后的激励为:
c[n]量化在CELP编解码器分配的大多数位中,意味着不能由线性预测或音高预测获得信息。在z域最终信号X(Z)可表示为:
8.5 噪声加权
大多数(即便不是全部)现代音频编解码器都会”形成“噪声,它大多出现在耳朵不能检测到的频域。例如,耳朵更能忍受噪声谱中较大声部分,反之亦然。为了获得最佳语音质量,CELP编解码器在感知加权域最小化噪声均方误差,所以可以在编码器中对误差信号应用一个感知噪声加权滤波器W(z)。在大多数CELP编解码器中,W(z)是一个由线性预测系数(LPC)派生而来零极点加权滤波器,一般用带宽阐述。令合成滤波器1/A(z)代表频谱包络,CELP编解码器典型地导出噪声加权滤波器为:
在Speex参考实现中y1=0.9且y2=0.6。如果滤波器A(z)在z平面有(复)极点pi,滤波器A(z/y)将有一个pi‘=ypi的极点。
加权滤波器应用于误差信号,用来通过analysis-by-synthesis(AbS)最优化码本搜索,这导致趋向于1/W(z)的噪声谱形。虽然这一简单模型是CELP很有效的重要原因,但W(z)却是感知最优噪声加权函数的粗糙近似。图8.2阐释了由图8.1得来的噪声谱形。在本手册中,W(z)指的是噪声加权滤波器而1/W(z)是噪声整形滤波器(或曲线)。
图8.2 CELP中标准噪声整形,任意y轴偏移
8.6 为分析合成技术
CELP中的一个主要原理叫Analysis-by-Synthesis(AbS),即编码(分析)是通过闭环感知最优解码(合成)信号实现的。理论上,最佳的CELP流应通过尝试所有可能的位组合并选择其中产生最佳听觉解码信号的那个组合产生。实际中这明显是不可能的,有两个原因:所需的复杂度超出目前所有可用的硬件,并且”最佳听觉“选择标准是人的听力,机器做不到。
为了利用有限的计算资源进行实时编码,CELP最优化利用感知加权函数分解成更小的、更易管理的、顺序的检索。









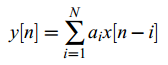
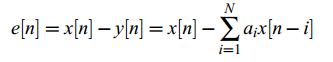
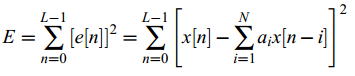
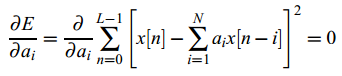
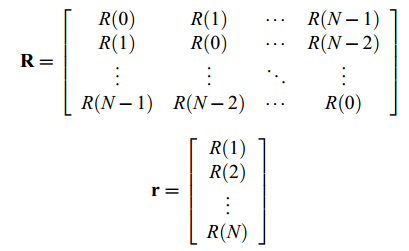
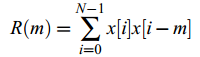
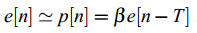


















 1454
1454

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








