运筹说 第67期 | 动态规划模型的建立与求解

通过前一期的学习，我们已经学会了动态规划的基本概念和基本原理。本期小编带大家学习动态规划模型的建立与求解。

动态规划模型的建立

一 概述

建立动态规划的模型，就是分析问题并建立问题的动态规划基本方程。

成功地应用动态规划方法的关键，在于识别问题的多阶段特征，将问题分解成为可用递推关系式联系起来的若干子问题，而正确建立基本递推关系方程的关键又在于正确选择状态变量，保证各阶段的状态变量具有递推的状态转移关系

二 例题展示

接下来小编将以资源分配问题为例介绍动态规划的建模条件及解法，详见例1。资源分配问题是动态规划的典型应用之一，资源可以是资金、原材料、设备、劳力等，资源分配就是将一定数量的一种或几种资源恰当地分配给若干使用者，以获取最大效益。

例1：某公司有资金10万元，若投资于项目的投资额为时，其收益分别为，问应如何分配投资数额才能使总收益最大?

首先这是一个与时间无明显关系的静态最优化问题，可列出其静态模型：

求，使，且满足约束

为了应用动态规划方法求解，可以人为地赋予它“时段”的概念。将投资项目排序，依次对项目1、2、3投资，即把问题划分为3个阶段，每个阶段只决定对一个项目应投资的金额，从而转化为一个3段决策过程。通常可以把决策变量定为原静态问题中的变量  ，即设

状态变量和决策变量有密切关系，状态变量一般为累计量或随递推过程变化的量。针对本例，可以把每阶段可供使用的资金定为状态变量，初始状态。为可分配用于第一种项目的最大资金，则当第一阶段（k=1）时，有

第二阶段（k=2）时，状态变量为余下可投资于其余两个项目的资金，即

一般地，当第k段时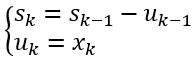

于是有

阶段k：本例中取1，2，3。

状态变量：第k段可以投资于第k项到第3个项目的资金。

决策变量 ：决定给第k个项目投资的资金。

状态转移方程：

指标函数：

最优指标函数 ：当可投资金为时，投资第k-3项所得的最大收益。

基本方程为

用动态规划方法逐段求解，便可得到各项目最佳投资金额， 就是所求的最大收益。

三 模型建立要点

1.分析题意，识别问题的多阶段特性，按时间或空间的先后顺序适当地划分为满足递推关系的若干阶段，对非时序的静态问题要人为地赋予“时段”概念。

2.正确地选择状态变量，使其具备两个必要特征：

（1࿰