杂记：Visual Tracking + Object Proposals + Features + Coding

这篇文章主要是做一个笔记式的讲解最近关注的一些东西，包括基于核相关滤波器的目标跟踪算法、EdgeBoxes目标假设算法、Color Names特征描述方法，最后再讲讲我对如何进行高效率编程的理解。

一、核相关滤波器   High-Speed Tracking with Kernelized Correlation Filters (KCF) PAMI15

    上面左图是一帧图像并给出了初始目标位置，右图红色框部分对应目标样本，然后我们对样本在两个不同方向上分别做循环移位，产生了右图中显示的其余样本。现在我们想拟合一个回归器，希望真样本的回归值最大，然后其它衍生样本的回归值随着循环移位长度的增加而递减，如下图所示：

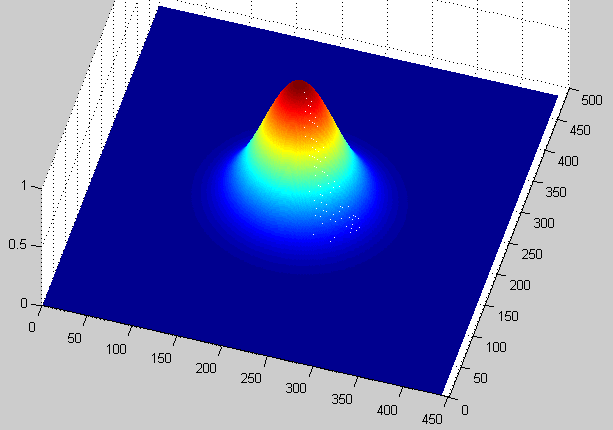
        上面右图显示的是期望的回归值，一般是一个高斯分布。

        试想一下，有了这么一个回归器（拟合函数），当输入目标样本图像时，它给出最高响应值，当输入一个由目标样本循环移位得到的衍生样本时，它给出一个相对较低的响应值，并且响应值随着移位量的增加而减小。那么这个回归器就可以用来做目标检测了，从而实现基于检测的跟踪。

        上图给出了线性峰度回归模型及其闭式解，其中大写X表示有所有样本组成的一个大矩阵。lambda是控制结构风险与经验风险比例的一个调节因子，lambda等于0时，该峰度回归器退化为一个线性回归器，即常说的最小二乘拟合。

        在求解该回归器的时候，需要对超大矩阵X和Y进行一系列运算，特别是矩阵求逆运算，非常耗时。X的每一行，即一个小x，它对应了一个图像样本，当样本采用HOG等高维特征表示时，x的元素个数非常多。

        所以从计算上来说，直接求解回归器不现实。但是循环矩阵理论为这一问题提供了解决方法。图中所示循环矩阵C(x)是一个由1维向量x衍生出的，其每一行是上一行的一个循环位移。循环矩阵的一个重要性质就是其特征值对应了xbar中各个元素，其中xbar表示x的离散傅里叶变换向量。而C(x)的特征向量对应离散傅里叶变换矩阵F的列向量。这里：xbar = F * x，即将向量x与矩阵F相乘就得到了x的傅里叶变换，关于离散傅里叶变换理论，大家可以查阅相关资料。

        当每个样本x_i都是由基本样本x经过循环移位得到时，大X就是一个循环矩阵：X=C(x)。在这种情况下，可以对回归器进行化简：

        上图是化简结果，可以看出在循环样本假设下，回归器可以在频率域快速求解，所有衍生样本x_i不再出现在回归器公式中，只需要知道基本样本小x的离散傅里叶变换向量即可。 然后带核的峰度回归器也能快速求解，具体可以参见KCF论文。求解出回归器以后，理论上可以对每个样本分别求取对应的回归值，选出回归值最高的样本作为检测（跟踪）结果。但是在循环样本假设下，检测过程可以同样非常快，因为我们只需评估一个样本的回归值，然后其它样本可以视为该基本样本的循环移位，对应的回归值可以通过傅里叶技巧得到。检测部分的细节也请参考原文。

二、EdgeBoxes目标假设 Edge Boxes: Locating Object Proposals from Edges(EdgeBoxes) ECCV14

        上面是一组用EdgeBoxes在图像中找到的目标假设，只画出了得分最高的前7个框。EdgeBoxes先检测图像中的边缘，然后将边缘连接成轮廓，最后在图像中寻找那些包含完整轮廓的个数较多的矩形窗作为检测输出。可以看出该方法能发现图像中的显著目标，但是也倾向于寻找尺寸更大的框。

        这里我们关注的不是该检测方法本身，而是它所依赖的高效率、高可靠性的边缘检测方法：Fast Edge Detection Using Structured Forests (Structured Edge Detector) PAMI15

        结构随机森林就是一个随机森林分类器，但是其输出的是结构信息（e.g.一个字符串，一个mask等）。随机森林是由多个决策树并联得到的，下面讲讲这个基本的决策树分类器：Decision Forests. A Unified Framework for Classification, Regression, Density Estimation, Manifold Learning and Semi-Supervised Learning. Microsoft 2011

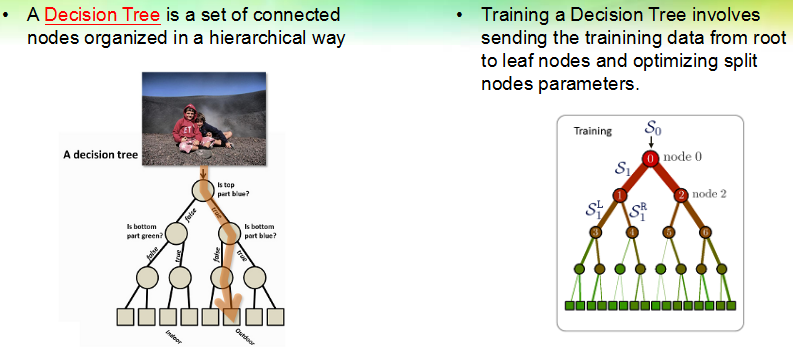
        一个决策树由一系列节点组成，包括最顶端的根节点、最末端的叶子节点，以及中间层的分离节点，根节点本身也属于分离节点。决策树执行分类任务的过程是简单明了的，如上面左图所示，样本输入到根节点，然后每个节点不断地重复着：问问题 -> 决定样本是该到左边还是右边。

      决策树是一颗二叉树，样本在树的节点之间流动，最终到达叶子节点，一个叶子节点对应一个决策结果，不同的叶子节点可以给出相同的决策。

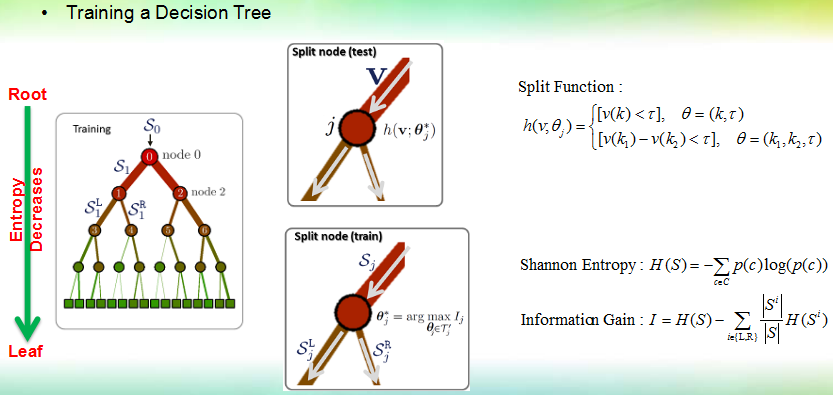
      比起使用决策树，其训练过程稍微复杂一点：准备了一组样本集和标签，如何确定每个节点的参数，使得最终能把样本集正确地分离开。

      决策树的训练过程就是依次确定各个分离节点的过程。一个分离节点有一个分离函数，常用形式有桩函数（stump），和差值函数（difference function），其中桩函数从样本向量中抽取一个维度（标量）然后用来和一个阈值tau做比较，来判断样本该去往左边还是右边，上图中[ ]是指示函数，输出0或1. 差值函数则从样本中抽取两个维度，然后作差并把差值和阈值做比较。

      分离节点的训练过程就是确定函数参数的过程，为了找到最佳的参数，需要定义一个目标函数，训练过程应该使得目标函数取得最大或最小值。常用的目标函数是信息增益，它是在香农熵的基础上定义的。熵是一个数据集纯净度的数值衡量——数据中类别数越多且各个类别比例越均衡，则熵越大，如果数据集只有一个类别，则熵最小。一个分离节点应该使得 离开这个节点的两个样本子集的熵之和 比 到达该该节点的训练集的熵更小