【笔记】robust MVDR-CSDN博客

本文链接：https://blog.csdn.net/Yenix92/article/details/134695262

MVDR波束形成具有较高SNR，但易受校准误差、导向矢量误差、相关矩阵估计误差等各种失配的影响，造成SOI损失。目前有不少研究致力于增加MVDR稳定性，基于个人有限的理解，现将这些论文整理成笔记。

[1] Robust Adaptive Beamforming Based on Steering Vector Estimation With as Little as Possible Prior Information

最优导向矢量可通过最大功率估计

$\underset{\mathbf{a}}{\rm{minimize}}\quad\mathbf{a}^H\hat{\mathbf{R}}^{-1}\mathbf{a}$

$\rm{subject\;to}\quad\mathbf{a}^H\tilde{\mathbf{C}}\mathbf{a}\leq\Delta_0,\;\Vert\mathbf{a}\Vert^2=N$

其中

$\Delta_0=\underset{\theta\in\Theta}{\rm{max}}\;\mathbf{d}^H(\theta)\tilde{\mathbf{C}}\mathbf{d}^H(\theta),\;\tilde{\mathbf{C}}=\int_{\tilde{\Theta}}\mathbf{d}(\theta)\mathbf{d}^{H}(\theta)\rm{d}\theta$

$\tilde\Theta$ 是 $\Theta$ 的补集， $\Theta$ 是SOI可能处在的方位，这里的重点是约束 $\mathbf{a}^H\tilde{\mathbf{C}}\mathbf{a}\leq\underset{\theta\in\Theta}{\rm{max}}\;\mathbf{d}^H(\theta)\tilde{\mathbf{C}}\mathbf{d}^H(\theta)$ 要求了导向矢量 $\mathbf{a}$ 在 $\Theta$ 中，而不会收敛到任何与干扰方向相关的导向矢量的线性组合中。上述QCQP问题转化成SDP问题求解

$\underset{\mathbf{a}}{\rm{minimize}}\;\rm{Tr}(\mathbf{R}^{-1}\mathbf{a}\mathbf{a}^H)$

$\rm{subject\;to}\;\rm{Tr}(\mathbf{a}\mathbf{a}^H)=N,\;\rm{Tr}(\tilde{\mathbf{C}}\mathbf{a}\mathbf{a}^H)\leq\Delta_0,\;\mathbf{a}\mathbf{a}^H\succeq\mathbf{0}$

论文中的仿真结果

算法复杂度为 $O(N^{4.5})$

[2] New Designs on MVDR Robust Adaptive Beamforming Based on Optimal Steering Vector Estimation

基于[1]所提出优化问题，作者提出增加少量的先验信息换取波束形成效果的提升，优化问题变为如下

$\underset{\mathbf{a}}{\rm{minimize}}\quad\mathbf{a}^H\hat{\mathbf{R}}^{-1}\mathbf{a}$

$\rm{subject\;to}\quad\mathbf{a}^H\tilde{\mathbf{C}}\mathbf{a}\leq\Delta_0,\;N(1-\eta_1)\leq\Vert\mathbf{a}\Vert^2\leq N(1+\eta_2)$

$\Vert\mathbf{Q}^H(\mathbf{a}-\mathbf{a}_0)\Vert^2\leq\varepsilon$

第二个约束相当于放宽了优化问题的可行域，取而代之是增加最优解与目标导向矢量相似性的约束，即这里的第三个约束， $\mathbf{Q}$ 定义的是广义相似性，论文里的仿真取最简洁的情况 $\mathbf{Q}=\mathbf{I}$ ，即 $\Vert(\mathbf{a}-\mathbf{a}_0)\Vert^2\leq\varepsilon$ ，约束条件描述的空间变为球体。这里增加的先验信息可以允许对目标导向矢量较粗略的估计，实际论文取 $\varepsilon=0.3N,\;\eta_1=\eta_2=0.5$ 是可以接受的，并不违背[1]所提出方法的初衷，即从最少的先验信息中得到最优导向矢量估计。麻烦的是这里的优化问题不是一个凸优化问题，实际上在 $\mathbf{Q}=\mathbf{I}$ 情况下，这里的QCQP问题转化成SDP问题后，可以得到全局最优解，但对于任意的 $\mathbf{Q}$ 则不能保证得到全局最优解。论文有大篇幅证明这里的QCQP等价于转化后的SDP，具体细节不在这里赘述。

作者另提出一个基准 $\Delta_1=\underset{\theta\in\Theta}{min}\;\mathbf{d}^H(\theta)\mathbf{C}\mathbf{d}(\theta),\;\mathbf{C}=\int_{\Theta}\mathbf{d}(\theta)\mathbf{d}^H(\theta)\rm{d}\theta$ ，将上面优化问题约束改成 $\mathbf{a}^H\tilde{\mathbf{C}}\mathbf{a}\leq\Delta_0$ 改成 $\mathbf{a}^H\mathbf{C}\mathbf{a}\geq\Delta_1$

实际上利用基准 $\Delta_0$ 和 $\Delta_1$ 都能有效地将导向矢量约束在期望导向区域的附近，远离干扰方向导向矢量的线性组合。对比[1]的优化方法（KVH beamformer），作者提出的两种方法略优。

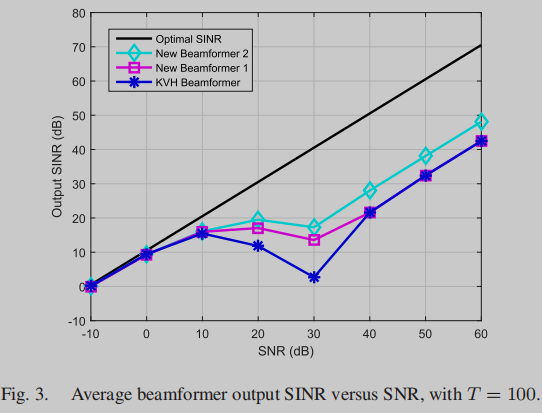
[3] Performance of DMI and Eigenspace-Based Beamformers

这篇介绍的算是特征空间波束成形的基础，假定有 $J$ 个干扰源，相关矩阵

$R_x=P_sS_dS_d^H+\sum_{j=1}^{J}P_{ij}S_{ij}S_{ij}^H+\sigma^2I=\sum_{i=1}^{M}\lambda_ie_ie_i^H$

其中特征值 $\lambda_1\geq\lambda_2\geq...\geq\lambda_{J+2}=...=\lambda_M=\sigma^2$ ，特征空间 $E_s=[e_1,e_2,...,e_{J+1}]$ 等价于信号干扰子空间，特征空间 $E_n=[e_{J+2},...,e_{M}]$ 则形成噪声子空间，利用 $S_d\perp\{e_{J+2},...,e_M\}$ ，可以将MVDR的加权改写成

$W=\mu R^{-1}S_d=\mu E_s\Lambda^{-1}E_s^HS_d$ ，其中 $\mu=[S_d^HE_s\Lambda^{-1}E_s^HS_d]^{-1}$

由于原论文没有考虑导向矢量失配，这里自己仿真了一下

导向矢量失配使在高输入SNR的情况下，MVDR的效果急剧下降。虽然这里提出的特征空间算法对比MVDR有一定提升，但没有解决导向矢量失配的问题，在高输入SNR的情况下并不如简单的对角加载。另外，尽管论文声称ESB在过度估计干扰数量的情况下仍有相当效果，但实际测试中干扰数量的估计对算法效果有较大影响。

[4] Robust MVDR Beamforming Using the DOA Matrix Decomposition

论文讨论的方法基本上是基于ESPRIT的源定位方法，这里先复习一下ESPRIT[5]

考虑两个子阵组成的阵列

$\mathbf{x}_1(t)=\mathbf{A}\mathbf{s}(t)+\mathbf{n}_1(t)$

$\mathbf{x}_2(t)=\mathbf{A\Phi}\mathbf{s}(t)+\mathbf{n}_2(t)$

假设有 $d$ 个声源， $\mathbf{\Phi}=\rm{diag}\{e^{j\gamma_1},e^{j\gamma_2},...,e^{j\gamma_d}\},\;\gamma_k=\omega\Delta\rm{sin}\theta_k/c$ ， $\mathbf{\Phi}$ 定义了 $d$ 个到达源的旋转不变性，很多地方在介绍ESPRIT的时候都用了ULA作为例子，其实线性阵列不是ESPRIT的硬性要求，但阵列必须可分为两个对源旋转不变的子阵， $\Delta$ 在这里定义了两个子阵的间距。也就是说简单的平移保留旋转不变性，但对阵列做旋转或对称操作就不保证旋转不变性，那最简单的方法就是先设计子阵1，再平移得到子阵2。整个阵列输出为

$\mathbf{x}(t)=\left[\begin{array}{c}\mathbf{x}_1(t)\\\mathbf{x}_2(t)\end{array}\right]=\left[\begin{array}{c}\mathbf{A}\\\mathbf{A\Phi}\end{array}\right]\mathbf{s}(t)+\left[\begin{array}{c}\mathbf{n}_1(t)\\\mathbf{n}_2(t)\end{array}\right]=\bar{\mathbf{A}}\mathbf{s}(t)+\mathbf{n}(t)$

对相关矩阵做特征分解

$\mathbf{R}=E[\mathbf{x}\mathbf{x}^H]=\mathbf{E}_s\mathbf{R}_s\mathbf{E}_s^H+\sigma^2\mathbf{I}$

由于 $\rm{span}\{\mathbf{E}_s\}=\rm{span}\{\bar{\mathbf{A}}\}$ ，必存在唯一非奇异的 $\mathbf{T}$ 使得 $\mathbf{E}_s=\bar{\mathbf{A}}\mathbf{T}$ ，则

$\mathbf{E}_s=\left[\begin{array}{c}\mathbf{E}_{s1}\\\mathbf{E}_{s2} \end{array} \right ]=\left[\begin{array}{c}\mathbf{AT}\\\mathbf{A\Phi T}\end{array}\right]$

由此可得 $\mathbf{E}_{s2}=\mathbf{E}_{s1}\mathbf{T}^{-1}\mathbf{\Phi T}=\mathbf{E}_{s1}\mathbf{\Psi}$ ，由于 $\mathbf{\Phi}$ 与 $\mathbf{\Psi}$ 相似， $\mathbf{\Psi}$ 的特征值一定是 $\mathbf{\Phi}$ 的对角元素， $\mathbf{\Psi}$ 通过最小二乘求解 $\mathbf{\Psi}=\mathbf{E}_{s1}^{\dagger}\mathbf{E}_{s2}$

而论文[4]中的方法是

$\mathbf{R}_{11}=E[\mathbf{x}_1\mathbf{x}_1^H]=\mathbf{AR}_s\mathbf{A}^H+\sigma^2\mathbf{I}=\mathbf{R}_{110}+\sigma^2\mathbf{I}$

$\mathbf{R}_{21}=E[\mathbf{x}_2\mathbf{x}_1^H]=\mathbf{A\Phi R}_s\mathbf{A}^H$

假设有 $q$ 个干扰源，其中 $\mathbf{R}_{110}$ 就是 $\mathbf{R}_{11}$ 最大的 $q+1$ 个特征值和对应特征向量构成的相关矩阵，若令 $(M-1)\times(M-1)$ 矩阵 $\mathbf{R}_d=\mathbf{R}_{21}\mathbf{R}_{110}^{\dagger}$ ，则 $\mathbf{R}_d$ 满足 $\mathbf{R}_d=\mathbf{A\Phi}\mathbf{A}^{-1}$ ，其中 $\mathbf{R}_{110}^{\dagger}=\sum_{i=1}^{q+1}\frac{1}{\mu_i}\nu_i\nu_i^H$ ，然后对 $\mathbf{R}_d$ 做特征分解，特征向量为 $\{\nu_i\}$ ，取修正的导向矢量为

$\mathbf{a}_r(\theta_0)=\underset{\nu_i}{\rm{argmax}}\frac{\mathbf{a}^H(\theta_0)\nu_i}{\vert\mathbf{a}^H(\theta_0)\vert\vert\nu_i\vert}$

这相当于通过ESPRIT做源定位，然后找出一个定位与期望来波方向最接近的，相应的特征向量作为导向矢量，注意 $\mathbf{R}_d$ 的特征向量就是组成 $\mathbf{A}$ 的向量。下一步是把相关矩阵关于 $\mathbf{a}_r=\nu_j$ 的特征值降到噪声水平，即

$\hat{\mathbf{R}}^{-1}=\sum_{i=1,i\neq j}^{M-1}\frac{1}{\mu_i}\nu_i\nu_i^H+\frac{1}{\sigma^2}\nu_j\nu_j^H$

先看结果

论文里没有明确说 $\mathbf{R}_{110}$ 是如何估计的，实际上无论是ESPRIT还是[4]中的方法都没有办法完全把信号干扰子空间和噪声子空间分离，信号干扰子空间不过是从输入的相关矩阵最大的 $q+1$ 个特征值对应的特征向量展开的空间估计，由于存在噪声，对于ESPRIT

$\rm{span}\{\mathbf{E}_{s}\}\neq\rm{span}\{\mathbf{A}\},\;\rm{span}\{\mathbf{E}_{s1}\}\neq\rm{span}\{\mathbf{E}_{s2}\}$

因此 $\mathbf{a}_r$ 是来波方向导向矢量的有偏估计。另外，不论 $\mathbf{a}_r$ 与 $\mathbf{a}_0$ 相差多少，输出总是保留 $\mathbf{a}_r$ 附近的信号，需要考虑进一步的限制，但若只按论文展示的结果看，效果还是可以的。

[6] Robust MVDR beamforming based on covariance matrix reconstruction

通常在其它文献中看到这篇文献的介绍都是一笔带过，最显赫的就是一条公式

$\tilde{\mathbf{R}}=\mathbf{R}-\frac{\mathbf{a}(\theta_0)\mathbf{a}(\theta_0)^H\mathbf{R}\mathbf{a}(\theta_0)\mathbf{a}(\theta_0)^H}{(\mathbf{a}(\theta_0)^H\mathbf{a}(\theta_0))^2}$

十分简洁，但实际上这篇论文还是挺有意思的。论文再一次说明了在低SNR下由于噪声存在，MVDR会更少地专注于抵消有导向矢量失配来波，但是在高SNR下，抵消效应就很明显了。由于希望来自 $\theta_0$ 方向的信号在导各种误差下不会被抵消，对角加载人为地加入噪声，这显然也削弱了对干扰信号的抑制，而论文采用的方法是从相关矩阵中减去期望来波方向的分量，但是这样做就不能保证 $\tilde{\mathbf{R}}$ 是半正定的。这里就指出了从半正定矩阵 $\mathbf{R}$ 减去一个rank-1的共轭对称矩阵

$\tilde{\mathbf{R}}=\mathbf{R}-\mathbf{vv}^H$

则 $\lambda_i(\tilde{\mathbf{R}})<\lambda_i(\mathbf{R})<\lambda_{i-1}(\tilde{\mathbf{R}})$ ，即 $\tilde{\mathbf{R}}$ 最多只有一个小于零的特征值。下一步就是考虑如何修正这个 $\tilde{\mathbf{R}}$ 让它成为半正定。论文用整整一页去证明对

$\tilde{\mathbf{R}}=\mathbf{R}-\lambda\frac{\mathbf{a}(\theta_0)\mathbf{a}^H(\theta_0)}{\Vert\mathbf{a}(\theta_0)\Vert^2}=\sum_{i=1}^{M}\mu_i\mathbf{u}_i\mathbf{u}^H_i,\mu_1\geq\mu_2\geq\ldots\geq\mu_M$ 有

$\underset{\lambda\rightarrow+\infty}{\rm{lim}}\frac{\vert\mathbf{a}^H(\theta_0)\mathbf{u}_M\vert}{\Vert\mathbf{a}(\theta_0)\Vert}=1$

这就是说对于 $\lambda\rightarrow+\infty$ ，来自 $\theta_0$ 方向的信号被完全保护起来，但过大的 $\lambda$ 会像对角加载那样削弱对干扰信号的抑制，实际上 $\lambda$ 的选择还是如第一条公式所示。而 $\mathbf{u}_M$ 的方向基本上是接近 $\mathbf{a}(\theta_0)$ 的，因此把 $\tilde{\mathbf{R}}$ 的最小的一个特征值变成噪声方差 $\sigma^2$ 它还是特征值中较小的一个，足以保护SOI。

Reference

[1] A. Kgabbazibasmenj, S. A. Vorobyov and A. Hassanien. Robust Adaptive Beamforming Based on Steering Vector Estimation With as Little as Possible Prior Information. IEEE Trans. Singal Process., vol. 60, no. 6, pp. 2974-2987. (2012)

[2] Y. Hunag, M. Zhou and S. A. Vorobyov. New Designs on MVDR Robust Adaptive Beamforming Based on Optimal Steering Vector Estimation. IEEE Trans. Singal Process., vol. 67, no. 14, pp. 3624-3638. (2019)

[3] L. Chang and C. Yeh. Performance of DMI and Eigenspace-Based Beamformers. IEEE Trans. Singal Process., vol. 40, no. 11, pp. 1336-1347. (1992)

[4] D. Li, Q. Yin, P. Wu and W. Guo. Robust MVDR Beamforming Using the DOA Matrix Decomposition. IEEE-ISAS 2011, pp. 105-110. (2011)

[5] R. Roy and T. Kailath. ESPRIT-Estimation of Signal Parameters Via Rotational Invariance Techniques. IEEE Trans. Singal Process., vol. 37, no. 7, pp. 984-995. (1989)

[6] P. Mu, D. Li, Q. Yin and W. Guo. Robust MVDR beamforming based on covariance matrix reconstruction. Sci. China Inform. Sci., vol. 56, 042303:1-042303:12. (2013)

Log
2023年11月29日 更新[1][2]
2023年11月30日 更新[3]
2023年12月4日  更新[4]
2023年12月6日  更新[6]