LeetCode – 3Sum — 题解

题干：

Problem:

Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note:
Elements in a triplet (a,b,c) must be in non-descending order. (ie, a ≤ b ≤ c)
The solution set must not contain duplicate triplets.

    For example, given array S = {-1 0 1 2 -1 -4},

    A solution set is:
    (-1, 0, 1)
    (-1, -1, 2)

1. Naive Solution

Naive solution is 3 loops, and this gives time complexity O(n^3). Apparently this is not an acceptable solution, but a discussion can start from here.

* The solution also does not handle duplicates. Therefore, it is not only time inefficient, but also incorrect.

Result:

Submission Result: Output Limit Exceeded

2. Better Solution

A better solution is using two pointers instead of one. This makes time complexity of O(n^2).

To avoid duplicate, we can take advantage of sorted arrays, i.e., move pointers by >1 to use same element only once.

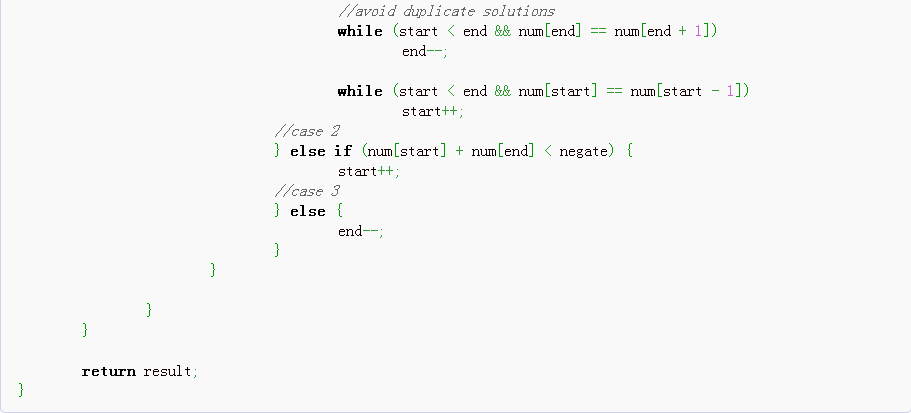
3. Wrong solution  version of right answer

I made a mistake when I code the right answer which causes an unaccepted trial. 

//3sum
  public List<List<Integer>> threeSum(int[] nums) {
        /*Wrong version
        //Sort Array
        Arrays.sort(nums);
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        */
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        //Sort Array
        Arrays.sort(nums);

        //i从0位置遍历到倒数第3个位置
        for(int i = 0; i < nums.length-2; i ++){
            //避免重复元素
            if(i == 0 || nums[i] > nums[i-1]) {
                int target = -nums[i];


                int start = i + 1;
                int end = nums.length - 1;
                //use the binary search
                while(start < end){
                    if(nums[start] + nums[end] == target){
                        List<Integer> temp = new ArrayList<Integer>();
                        temp.add(nums[i]);
                        temp.add(nums[start]);
                        temp.add(nums[end]);

                        list.add(temp);
                        start++;
                        end--;
                        //avoid duplicate
                        while(start < end && nums[end] == nums[end+1])
                            end--;
                        while(start < end && nums[start] == nums[start-1])
                            start++;
                    }else if(nums[start] + nums[end] < target){
                        start++;
                    }else{//nums[start] + nums[end] > target
                        end--;
                    }
                }
            }
        }
        return list;
    }

* The solution also does not handle duplicates. Therefore, it is not only time inefficient, but also incorrect.

转自：http://www.programcreek.com/2012/12/leetcode-3sum/

这篇也写得不错，思路可参考：http://www.cnblogs.com/springfor/p/3859670.html

文章有改动。