【面试题之算法部分】深入快速排序

最新推荐文章于 2022-03-16 16:20:48 发布

YoungLeoo

最新推荐文章于 2022-03-16 16:20:48 发布

阅读量2.2k

点赞数

分类专栏：面试题之庖丁解牛文章标签：快速排序面试题算法递归

本文链接：https://blog.csdn.net/YoungLeoo/article/details/47954967

版权

面试题之庖丁解牛专栏收录该内容

8 篇文章 0 订阅

订阅专栏

本篇文章我将讲述快速排序的基本思想，实现，和时间复杂度的深入分析。

基本思想：选取待排序列中的某个元素t，然后按照与该元素的大小关系重新整理序列中的元素，使得整理后的序列中排在t以前的元素均小于t，排在t以后的元素均大于等于t，我们将t称为划分元素。此时可以保证此时t的位置一定和最终有序序列t的位置相同，故我们可以选取t以前和以后的两个子序列作为新的序列去做同样的处理。不断递归去处理直至每个元素都调整到它对应的位置上，最终使得整个序列有序。

由以上可知，快速排序是通过反复的对原序列进行划分来达到排序的目的，所以快排是一种基于划分的排序方法。

下面给出两个不同版本的实现：

//1.《算法导论》上的实现

QUICKSORT(A, p, r)
if p < r
    q = PARTITION(A, p, r)
    QUICKSORT(A, p, q-1)
    QUICKSORT(A, q+1, r)

PARTITION(A, p, r)
x = A[r];
i = p-1;
for j = p to r-1
    if A[j] <= x
        i = i + 1
        exchange A[i] wich A[j]
exchange A[i+1] with A[r]
return i+1

划分过程详解：
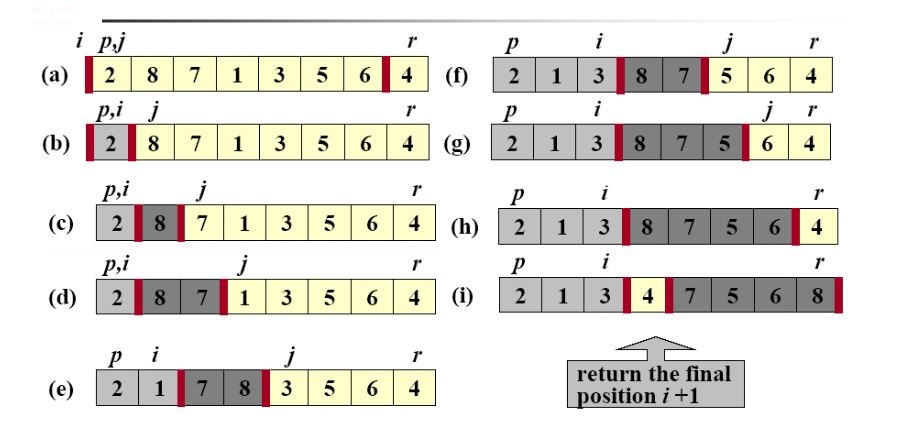
Partition总是选择一个x=A[r]作为主元，并围绕它来划分子数组A[p…r]，随着程序的执行，数组被划分成4个（可能有空的）区域。for循环的每一轮迭代的开始，每一个区域都满足都满足一定的性质：
1.若p <=k <= i，则A[k] <= x。
2.若i+1 <= k <= j-1，则A[k] > x。
3.若 j <= k <= r-1，则A[k]可能为任意一种情况。
4.若 k=r，则A[k] = x。
划分过程示例：
这里写图片描述

//2.另一种更常用的实现
void quickSort(int A[], int lo, int hi)
{
    if(lo >= hi) return;
    int i = lo, j = hi;
    int tmp = A[lo];
    while(i < j)
    {
        while(i < j && tmp <= A[j]) j--;
        if(i < j) s[i++] = s[j];
        while(i < j && tmp > A[i]) i++;
        if(i < j) s[j--] = s[i];
    }
    s[i] = tmp;
    quickSort(A, lo, i-1);
    quickSort(A, i+1, hi);
}

第二个版本有它的局限性：如果要求用单链表来实现快速排序时，由于没有父指针，需要确定递归左区间的第二个参数(即处于i-1处的节点)，需要O（n）的时间来查找，降低了快速排序的时间复杂度。

下面是单链表来实现快排的代码：

struct node{
    int key;
    node *next;
    node(int nKey, node *pNext) : key(nkey), next(pNext){}
};

node *partion(node *begin, node *end)
{
    int key = begin->key;
    node *p = begin;
    node *q = p->next;
    while(q != end)
    {
        if(q->key < key)
        {
            p = p->next;
            swap(p->key, q->key);
        }
        q = q->next;
    }
    swap(p->key, begin->key);
    return p;
}

void quickSort(node *begin, node *end)
{
    if(begin != end)
    {
        node *mid = partion(begin, end);
        quickSort(begin, mid);
        quickSort(mid->next, end);
    }
}

时间复杂度分析：

在最坏情况下，n个元素的数组被切分为n-1个元素和0个元素的两部分，PARTITION因为要经历n-1次迭代，所以运行代价为Ө(n)。即：T(n) = T(n-1) + T(0) + Ө(n) = T(n-1) + Ө(n)　（元素数为0时，QUICKSORT直接返回，所以运行代价为Ө(1)，利用代换法，可以得到最坏情况下快速排序算法的运行时间为Ө(n^2)。

在最好情况下，每次PARTITION都得到两个元素数分别为floor(n/2)和ceiling(n/2)-1的子数组，这种情况下：T(n) ≤ 2*T(n/2) + Ө(n)，所以最佳情况下快速排序算法的运行时间为Ө(n*lg(n))。

考虑平均情况，假设每次都以9:1的例划分数组，则得到：
T(n) ≤ T(9*n/10) + T(n/10) + Ө(n)
它的递归树如下：
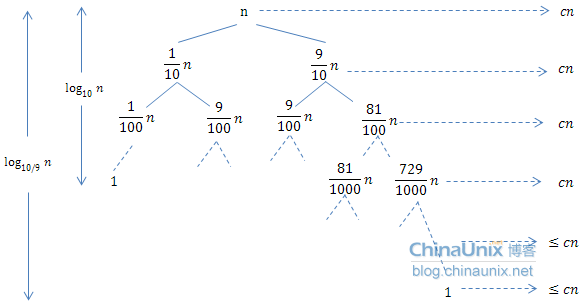
这里写图片描述
树的到最近的叶结点的路径长度为log_10(n)，在这层之前这棵树每层都是满的，所以运行时间为cn，而越往下直至最底层log_(10/9) (n)，每层的代价都会小于cn。所以以9:1划分情况下，总的运行时间
T(n) ≤ log_(10/9) (n) = O(lg(n))
事实上只要以常数比例划分数组的情况，哪怕是99:1，运行时间也仍然为O(lg(n))，只不过O记号中隐含的常量因子要大些。而一般情况下，平均下来的划分情况不应该比9:1差，直观上看来平均情况下快速算法的运行时间为O(lg(n))。

下面来分析一下平均情况。快速排序主要在递归地调用PARTITION过程。我们先看下PARTITION调用的总次数，因为每次划分时，都会选出一个主元元素（作为基准、将数组分隔成两部分的那个元素），它将不会参与后续的QUICKSORT和PATITION调用里，所以PATITION最多只能执行n次。在 PARTITON过程里，有一段循环代码（第3至第8行，将各元素与主元元素比较，并根据需要将元素调换）。我们把这段循环代码单独提出来考虑，这样在每次PATITIOIN调用里，除循环代码外的其它代码的运行时间为O(1)，所以在整个排序过程中，除循环代码外的其它代码的总运行时间为O(n*1) = O(n)。

接下来分析整个排序过程中，上述循环代码的总运行时间（注意：不是某次PATITION调用里的循环代码的运行时间）。可以看到在循环代码里，数组中的各个元素之间进行比较。设总的比较次数为X，因为一次比较操作本身消耗常量时间，所以比较的总时间为O(X)。如此整个排序过程的运行时间为O(n+X)。

为了得到算法总运行时间，我们需要确定总的比较次数X的值。为了便于分析，我们将数组A中的元素重新命名为 z_1，z_2，z_3，…，z_n。其中z_i是数组A中的第i小的元素。此外，我们还定义Z_i_j = {z_i, z_(i+1), …, z_j}为z_i和z_j之间（包含这两个元素）的元素集合。

我们用指示器随机变量X_i_j = I{z_i与z_j进行比较}。这样总的比较次数：
X = ∑ ∑ X_i_j
求期望得：
E[X] = E[∑ ∑ X_i_j] = ∑ ∑ E[X_i_j] = ∑ ∑ Pr{z_i与z_j进行比较}

注意两个元素一旦被划分到两个不同的区域后，则不可能相互进行比较。它们能进行比较的条件只能为：z_i和z_j在同一个区域，且z_i或z_j被选为主元元素，这样：
Pr{z_i与z_j进行比较} = Pr{z_i或z_j是从Z_i_j中选出的主元元素} = Pr{z_i是从Z_i_j中选出的主元元素} + Pr{z_j是从Z_i_j中选出的主元元素}
= 1/(j-i+1) + 1/(j-i+1) = 2/(j-i+1)　（因为两事件互斥，所以概率可以直接相加）

得到x_i_j的概率后，就可以得到总的比较次数：
E[X] = ∑ ∑ Pr{z_i与z_j进行比较} = ∑ ∑ 2/(j-i+1)
设变量k = j - 1，则上式变为：
E[X] = ∑ ∑ 2/(k+1)
< ∑ ∑ 2/k
= ∑ O(lg(n)) （调合级数求和）
= O(n*lg(n))

所以在平均情况下快速排序的运行时间为O(n*lg(n))。

参考资料：
1.《算法导论》
2.http://blog.sina.com.cn/s/blog_73428e9a01017f9x.html