排序算法之 冒泡排序 及其时间复杂度和空间复杂度

        冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端，故名。

算法分析

        冒泡排序算法是所有排序算法中最简单的（前面也提到过），在生活中应该也会看到气泡从水里面出来时，越到水面上气泡就会变的越大。在物理上学气压的时候好像也看到过这种现象；其实理解冒泡排序就可以根据这种现象来理解：每一次遍历，都把大的往后面排（当然也可以把小的往后面排），所以每一次都可以把无序中最大的（最小）的元素放到无序的最后面（或者说有序元素的最开始）；

        基本步骤：

     1、外循环是遍历每个元素，每次都放置好一个元素；　　　

     2、内循环是比较相邻的两个元素，把大的元素交换到后面；

     3、等到第一步中循环好了以后也就说明全部元素排序好了；

代码实现

 #include<stdio.h>
 //打印数组元素
 void print_array(int *array, int length)
 {
     int index = 0;
     printf("array:\n");
     for(; index < length; index++){
         printf(" %d,", *(array+index));
     }   
     printf("\n\n");
 }
 
 void bubbleSort(int array[], int length)
 {
     int i, j, tmp;
     
     if (1 >= length) return;// 判断参数条件
 
     for (i = length-1; i > 0; i--){//外循环，循环每个元素
         for (j = 0; j < i; j++){  // 内循环，
             if (array[j] > array[j+1]){// 交换相邻的两个元素
                 tmp        = array[j];
                 array[j]   = array[j+1];
                 array[j+1] = tmp;
             }   
         }   
     }   
 }

 int main(void)
 {
     int array[12] = {1,11,12,4,2,6,9,0,3,7,8,2};
     print_array(array, 12);
     bubbleSort(array, 12);
     print_array(array, 12);
     return 0;
 }

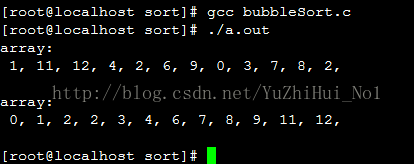
运行结果：

时间复杂度

        这个时间复杂度还是很好计算的：外循环和内循环以及判断和交换元素的时间开销；

       最优的情况也就是开始就已经排序好序了，那么就可以不用交换元素了，则时间花销为：[ n(n-1) ] /  2；所以最优的情况时间复杂度为：O( n^2 )；

       最差的情况也就是开始的时候元素是逆序的，那么每一次排序都要交换两个元素，则时间花销为：[ 3n(n-1) ] / 2；（其中比上面最优的情况所花的时间就是在于交换元素的三个步骤）；所以最差的情况下时间复杂度为：O( n^2 )；

        综上所述：

       最优的时间复杂度为：O( n^2 ) ；有的说 O(n)，下面会分析这种情况；

       最差的时间复杂度为：O( n^2 )；

       平均的时间复杂度为：O( n^2 )；

空间复杂度

      空间复杂度就是在交换元素时那个临时变量所占的内存空间；

     最优的空间复杂度就是开始元素顺序已经排好了，则空间复杂度为：0；

     最差的空间复杂度就是开始元素逆序排序了，则空间复杂度为：O(n)；

     平均的空间复杂度为：O(1)；

最优时间复杂度 n

        有很多人说冒泡排序的最优的时间复杂度为：O(n)；其实这是在代码中使用一个标志位来判断是否已经排序好的，修改下上面的排序代码：

 void bubbleSort(int array[], int length)
 {
     int i, j, tmp;
     int flag = 1;
     
     if (1 >= length) return;
 
     for (i = length-1; i > 0; i--, flag = 1){ 
         for (j = 0; j < i; j++){
             if (array[j] > array[j+1]){
                 tmp        = array[j];
                 array[j]   = array[j+1];
                 array[j+1] = tmp;
                 flag = 0;
             }   
         }   
         if (flag) break;
     }   
 }

        根据上面的代码可以看出，如果元素已经排序好，那么循环一次就直接退出。或者说元素开始就已经大概有序了，那么这种方法就可以很好减少排序的次数；其实我感觉这种方法也有弊端，比如 要额外的判断下，以及赋值操作；

空间复杂度为 0

        有人会说这个空间复杂度能降到0，因为空间复杂度主要是看使用的辅助内存，如果没有辅助内存变量，那么可以说空间复杂度为0；所以该算法中空间复杂度一般是看交换元素时所使用的辅助空间；

       1、 a  = a + b； b = a - b； a = a - b；

       2、 a = a * b；   b =  a / b； a = a / b；

       3、 a = a ^ b；  b =  a ^ b；a = a ^ b； 

       上面几种方法都可以不使用临时空间来交换两个元素，但是都有些潜在的问题，比如 越界；所以个人觉得还是老老实实的用个临时变量吧，这样算法意图就比较清晰了。

     转载请注明作者和原文出处，原文地址：http://blog.csdn.net/yuzhihui_no1/article/details/44339711#t5

     若有不正确之处，望大家指正，共同学习！谢谢！！！