08_排序之归并、快速

1.归并排序

使用分治思想

public static void mergeSort(int[] A, int n){
    int[] B = new int[A.length];
    mergeSort_c(A, 0, n - 1, B);
}

public static void mergeSort_c(int[] A, int left, int right, int[] B){
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort_c(A, left, mid, B);
        mergeSort_c(A, mid + 1, right, B);
        merge(A, left, mid, right, B);
    }
}

public static void merge(int[] A, int left, int mid, int right, int[] B){
    int i = left, j = mid + 1, k = 0;
    while (i <= mid && j <= right)
        if (A[i] <= A[j])
            B[k++] = A[i++];
        else
            B[k++] = A[j++];
    while (i <= mid) B[k++] = A[i++];
    while (j <= right) B[k++] = A[j++];

    //拷贝
    k = 0;
    int t = left;
    while (t <= right) A[t++] = B[k++];
}

归并排序是稳定的排序算法

时间复杂度分析，如何分析递归的时间复杂度
假设a可以分解为多个子问题b,c，那么b,c解决后，就可把b,c的结果合并成a的结果，递推式如下

T(a) = T(b) + T(c) + K

其中K表示将二者合并所需的时间
下面对n个元素进行分析，假设n个元素进行归并排序需要的时间是T(n)，那么分解成两个子数组排序的时间都是T(n/2)，我们知道，merge()函数合并两个有序子数组的时间复杂度是O(n)，所以归并排序的时间复杂度计算式为

T(1) = C;                       //C为常量级
T(n) = 2*T(n/2) + n;      // n>1

T(n) = 2 * T(n/2) + n
     = 2*(2 * T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 2^k * T(n/2^k) + k*n

当 T(n/2^k)=T(1) 时，也就是 n/2^k=1，我们得到 k=log2n 。我们将 k 值代入上面的公式，得到 T(n)=Cn+nlog2n 。如果我们用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

归并排序的空间复杂度。使用了一个辅助数组B，大小与A相同，故空间复杂度为O(n)，这是归并的一个缺点

2.快速排序

先思考递推公式

递推公式：
quick_sort(left…right) = quick_sort(left…mid-1) + quick_sort(mid+1… right)

终止条件：
left >= right

我们遍历left到right之间的数据，把小于pivot的放到左边，大于pivot的放到右边，pivot放到中间。这样，数组就被分成了三部分，前面left到mid-1之间都是小于pivot的，中间是pivot，后面mid+1到right之间是大于pivot的。
接着，我们递归的处理left到mid-1和mid+1到right的数据，直到区间缩小为1。
（注：这里的mid使用不太准确，因为pivot不一定每次都能完美中分）

public static void quickSort_c(int[] A, int left, int right){
    if (left >= right) return;
    int mid = partition(A, left, right);
    quickSort_c(A, left, mid - 1);
    quickSort_c(A, mid + 1, right);
}

关于piovt中分值的选择，我们这里选择数组末尾
partition分区函数是本排序公式的关键，我们可以用O(n)的空间复杂度完成（申请两个临时数组），也可以优化到原地排序，下面讲解原地排序的方法
我们用游标i把A[left,right-1]分成两部分，A[left,i-1]是小于pivot的，叫做“已处理区间”,A[i,right-1]是“未处理区间”。每次从未处理区间A[i,right-1]中取一个元素A[j]，与pivot对比，如果小于pivot，则将其加入已处理区间的尾部，也就是A[i]的位置。
数组的插入操作我们采用交换来省时， 只需要将 A[i]与 A[j]交换，就可以在 O(1) 时间复杂度内将 A[j]放到下标为 i 的位置。
如下图所示

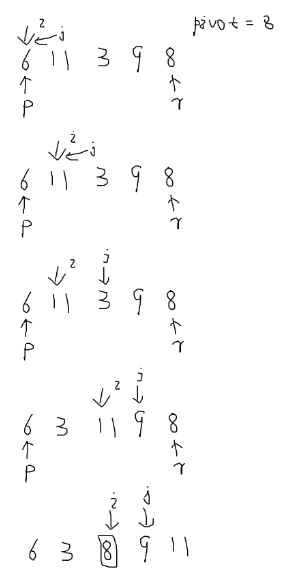
//实现原地排序
public static int partition(int[] A, int left, int right){
    int pivot = A[right];
    int i = left; //把数组分成“已处理”和“未处理”两个部分
    for (int j = left;j < right;j++){
        if (A[j] < pivot){
            int tmp = A[i];
            A[i] = A[j];
            A[j] = tmp;
            i++;
        }
    }
    int temp = A[i];
    A[i] = A[right];
    A[right] = temp;


    return i;
}

提问：快速排序是不是一个稳定的算法？
如下图所示

两个6的位置发生了改变，故并不是一个稳定的算法

3.归并与快排的区别

（1）归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。
（2）归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。

归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法，这也使它存在致命的缺点，即归并排序不是原地排序算法，空间复杂度比较高，是 O(n)。正因为此，它也没有快排应用广泛。
快速排序算法虽然最坏情况下的时间复杂度是 O(n2)，但是平均情况下时间复杂度都是 O(nlogn)。不仅如此，快速排序算法时间复杂度退化到 O(n2) 的概率非常小，我们可以通过合理地选择 pivot 来避免这种情况。

4.快排的时间复杂度分析

如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递归求解公式和归并相同，为O(nlogn)

T(1) = C；   n=1时，只需要常量级的执行时间，所以表示为C。
T(n) = 2*T(n/2) + n； n>1

但想要正好一分为二，是很难实现的
如果数组已经有序，如1，2，3，4，5，6，每次选择最后一个元素作为pivot，那每次得到的两个区间都是不均等的。大约需要n次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约n/2个元素，这种情况下，快排的时间复杂度就从O(nlogn)退化成了O(n2)

那么，平均情况呢？
需要使用递归树，暂时不讲，平均情况为O(nlogn)

5.如何在O(n)时间复杂度内求无序数组的第K大元素

我们选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot，对数组 A[0…n-1]原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。
如果 p+1=K，那 A[p]就是要求解的元素；如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间，我们再按照上面的思路递归地在 A[p+1…n-1]这个区间内查找。 同理，如果 K < p+1,那我们就在A[0…p-1]区间查找。

时间复杂度分析
第一次分区查找，对大小为n的数组执行操作，需要遍历n个元素，第二次分区查找，只需要对大小n/2的数组执行操作，需要遍历n/2个元素…依此类推，分区遍历元素的个数分别为n/4,n/8,n/16…直到区间缩小为1.
每次分区遍历的元素个数加起来，就是n+n/2+n/4+…+1，等比数列求和，等于2n-1，所以，上述解决思路的时间复杂度就为 O(n)。

参考课程：极客时间王争老师的《数据结构与算法之美》