康托编码

最新推荐文章于 2022-01-28 14:24:17 发布
最新推荐文章于 2022-01-28 14:24:17 发布
阅读量4.5k 收藏 2
点赞数 2
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ZIFENGCHUANSHUO007/article/details/38902123
版权
康托编码是一种高效解决n个数全排列中第k个位置数值的方法，具有O(n)的时间复杂度。通过康托展开的逆过程，可以得知给定全排列数在所有排列中的顺序。例如，求解321是第6小的全排列。代码实现是通过解线性递推关系找出具体数值。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

n个数的全排列，按照从下到大的顺序排列，问第k个位置的数是多少？

这个问题有几种方法，不过只有康托编码的时间复杂度是最低的。是O(n),简直凶残。

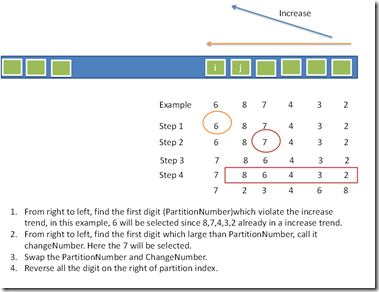
1.用next_permutation来求，这个也是leetcode上的一道题，就是求其下一个排列，然后对1234…n 运行n次 next_pernutation方法就能得到第k个数了

image

思想就是这样。

2.利用康托编码来求。

其实就是康托展开的逆过程。

康托展开用来求某个全排列数是第几小的数，也就是当这些数按顺序排时第几个数。

过程如下：比如求321 是 第几小的，可以这样来想：小于3的数有1和2 两个，首位确定之后后面两位有2！中情况，所以共有2*2！=4种。

小于2的数只有一个1，所以有1*1！=1种情况，最后一位是1，没有比一小的数，所以是0*0！=0

综上：小于321的数有4+1=5个，所以321是第六小的数。</

最低0.47元/天 解锁文章
Matafight
关注
康托编码与解码
Bazingaea的博客
03-05 1085
原文地址：https://blog.csdn.net/neutre/article/details/78065633 对于一个集合 {1,2,3，…，n}，很明显它有 n! 种全排列， 把它们全都按照字典序排好序（从小到大），对应顺序{1,2,3，…，n!}， 假如问你第X个全排列是什么，或者某个全排列在其中的序号是多少，可以利用康拓展开式来求。 康托展开式： X = a[n]*(n-1...
全排列的编码与解码——康托展开
uDon的博客
09-22 900
对于一个集合 {1,2,3，…，n}，很明显它有 n! 种全排列， 把它们全都按照字典序排好序（从小到大），对应顺序{1,2,3，…，n!}， 假如问你第X个全排列是什么，或者某个全排列在其中的序号是多少，可以利用康拓展开式来求。康托展开式： X = a[n]*(n-1)! + a[n-1]*(n-2)! + … + a[i]*(i-1)! + … + a[2]*1! + a[1]*0! 康
全排列的编码与解码——康托展开 (附完整代码)
AC，∑ndless
11-23 8362
一、康托展开：全排列到一个自然数的双射 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! ai为整数，并且0  适用范围：没有重复元素的全排列 二、全排列的编码： {1,2,3,4,...,n}的排列总共有n!种，将它们从小到大排序，怎样知道其中一种排列是有序序列中的第几个？ 如 {1,2,3} 按从小到大排列一共6个：
WIKIOI – 1083 Cantor表
weixin_33853827的博客
04-28 161
题目描述Description 现代数学的著名证明之一是Georg Cantor证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的： 1/1 1/2 1/3 1/4 1/5 … 2/1 2/2 2/3 2/4 … 3/1 3/2 3/3 … 4/1 4/2 … 5/1 … … 我们以Z字形给上表的每一项编号。第一项是1/1，然后是1/2，2/1，3/...
排列的编码【康托展开】
stoorz
07-09 561
题目大意： InputInputInput (4,(3,2,1,4)) (5,(3,5,1,2,4)) -1 OutputOutputOutput 15,67 思路： 考试时居然把这道题推出来了。。。 然后还AK了。。。 正题： 这道题要我们求出这个排列是字典序第几大的，也就是让我们求 有多少个排列比该排列小，再加1即是答案。 那么应该如何考虑呢？ 举个例...
结合力扣题目：第k个排列，学习康托展开和逆康托展开
01-20
讲述康托编码之前，需要先学习一下康托展开，康托展开是一个全排列到自然数的一个双射，说白了就是将一堆数从小到大排列，然后计算比某个排列数小的排列数有多少个，或者加1来计算某个排列数所在的位置。 公式： ...
N 和 N^2 之间的三种不同的双射或配对函数（包括康托多项式）：配对函数：将两个自然数编码为一个自然数（反之亦然）-matlab开发
05-30
Bijection_Pairing_N_N2(index_In,flag_Pair) 在 [0,...,K] 和 N^2 的一些持续增长的子集之间提供三种不同的显式双射（根据三种模式：康托或三角形、优雅或方形、二次幂- Odd 或 POTO 用于 2-adic 整数分解）。...
康托编码（模板）
qq_44866969的博客
11-04 205
//O(n)求1~n全排列字典序第k小，例如n=3，则123为k=1，132为k=2 void init(){ //预处理阶乘 fac[0]=1; for(int i=1;i<=17;i++){ fac[i]=fac[i-1]*i; } } vector<int> Kthpermutation(int n,ll k){ //一种全排列，例如n=6，则k=t1*5!+t2*4!+t3*3!+t4*2!+t5*1!+t6*0!+1 //ti=比第i位上的数字小且没有在小于.
经典算法之cantor数表
07-08
本题为一个比较简单的数学基础算法，找规律题目。适合那些算法刚入门的同学参考一下。
全排列的编码与解码——【康托展开及其逆运算】
*乘号的笔记本
04-04 643
参考过程：点击打开链接 参考代码：点击打开链接 康托展开表示的是当前排列在n个不同元素的全排列中的名次。比如213在这3个数所有排列中排第3。   那么，对于n个数的排列，康托展开为：   其中表示第i个元素在未出现的元素中排列第几。举个简单的例子：   对于排列4213来说，4在4213中排第3，注意从0开始，2在213中排第1，1在13中
【GDOI2003】排列的编码 {康托展开+高精度}
Nowed
07-09 270
题目 Description 　　对于n个元素的排列P=(p1,p2,……,pn)，请你编写一个程序，在不构造出所有排列的情况下，直接输出该排列在按字典序排列的字典中的序数d(p),其中p1∈{1,2,3,…,n},1&amp;amp;amp;amp;lt;=n&amp;amp;amp;amp;lt;=50。例如：n=4,若p=(2,3,4,1)，则d(p)=10;若p=(4,2,1,3),则d(p)=21 Input 　　每一行对应一个数据，格式为(...
Cantor的数表
tan313的专栏
06-15 880
题目描述 如下数列，前5项分别是1/1，1/2，2/1，3/1，2/2……。输入n，输出第n项。 1/1   1/2   1/3   1/4   1/5 2/1   2/2   2/3   2/4 3/1   3/2   3/3 4/1   4/2 5/1 样例输入 3 14 7 12345 样例输出 2/1 2/
全排列的编码与解码——康托展开及其逆展开
foradawn的博客
11-13 607
一、康托展开：全排列到一个自然数的双射   X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0!   ai为整数，并且0<=ai<i(1<=i<=n)    适用范围：没有重复元素的全排列     二、全排列的编码：   {1,2,3,4,...,n}的排列总共有n!种，将它们从小到大排序，怎样知道其中一种排列是有序序
洛谷 P1014 [NOIP1999 普及组] Cantor 表 | OpenJudge NOI 2.1 8760:Cantor表
君义NOIP的博客
01-28 815
【题目链接】 洛谷 P1014 [NOIP1999 普及组] Cantor 表 【题目考点】 1. 二维数组 2. 找规律 3. 两下标间元素数量 数组中下标a到下标b间元素个数n（包括下标a和下标b的元素） n = b-a+1 【解题思路】 先为每条斜线编号 假设有一个焦点位置不断移动，每移动一次，编号加1。 根据题目中给定的编号规律，可以得知： 当i为奇数时：焦点从i/1出发，从左下到右上移动到1/i 当i为偶数时：焦点从1/i出发，从右上到左下移动到i/1 第1条斜线上有1/1，1个格子 第2条
算法之我见 [康托展开] 排列编号
weixin_30542079的博客
08-24 97
问题描述：对于1~N的序列来说，将他的全排列升序编号，问第n排列是怎样的，或者给一个排列问是第几个序列？ 关键思想：这种问题可以用康托展开来解决，其关键思想其实很简单，说白了就是简单的排列组合。 我们先来写下1~4的全排列感受一下{ 　　1 2 3 4 1 2 4 3 1 3 2 4 1 3 4 2 1 4 2 3 ...
数学基础2---cantor数表
weixin_44606952的博客
08-02 445
题目描述： 如下列数，第一项是1/1，第二项是1/2，第三项是2/1，第四项是3/1，第五项是2/2，……。输入一个数n输出第n项数表的数； 表的顺序描述，这个表是斜着看，就从右上方斜着到左下方； 1/1 1/2 1/3 1/4 1/5 2/1 2/2 2/3 2/4 3/1 3/2 3/3 4/1 4/2 5/1 样例输入： 3 7 14 12345 样例输出： 2/1 4/1 4/...
康托展开公式
最新发布
03-11
### 康托展开公式及其计算方法 康托展开是一种用于解决排列组合问题中的编码方式，它能够唯一表示一个特定的排列。具体来说，给定一组不重复的元素组成的序列，可以通过康托展开将其映射成自然数范围内的某个整数值。 对于长度为 \( n \) 的不同字符构成的字符串或者数组而言，其康托展开值 X 可以通过下面的表达式来定义： \[ X=a_n\cdot(n-1)!+a_{n-1}\cdot(n-2)!+\ldots+a_i\cdot(i-1)!+\ldots+a_2\cdot1!+a_1\cdot0!\tag{1} \] 其中 \( a_i \) 表示当前位右侧小于该位置上数字的数量[^4]。 为了更好地理解这一过程，考虑如下伪代码实现： ```python def cantor_expansion(permutation): from math import factorial result = 0 for i in range(len(permutation)): smaller_count = sum(1 for j in permutation[i + 1:] if j < permutation[i]) result += smaller_count * factorial(len(permutation) - i - 1) return result ``` 上述函数接收一个列表 `permutation` 参数并返回对应的康托展开值。这里遍历输入序列每一个元素，统计右边有多少个小于自己的数，并乘以其所在位权重即剩余项阶乘之积累加至最终结果中[^5]。 值得注意的是，当涉及到实际编程实践时，通常会预先准备好各个可能因子（\( (n-i)! \)，\( i=0,\dots,n-1 \)），以便提高效率[^3]。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值