MATLAB数值分析学习笔记：黄金分割法

在工程上，最优化就是使被研究对象尽可能高效的过程，比如使时间花费最少，设计出最多的产品。在数学上，最优化就是寻找函数在某一区间上的局部极值，这些函数具有一个或多个变量，具有单自变量的函数，该过程被称为一维优化问题，否则称之为多维优化问题。

对于一维优化问题，在数学上往往是通过求解函数的导数，极值点导数为0，来求解的，这就变成了导数求根的问题了，可以使用划界法和开方法。

在划界法中，有一种方法被广泛应用，它就是黄金分割法。

下以黄金分割法求解极小值为例，就原理，代码实现，问题求解三个方面向大家介绍。

原理

至于黄金分割法有什么好处，为什么必须用黄金分割数这个特别的比例呢？黄金分割法的优点将在下文逐渐浮出水面。

定区间：黄金分割法首先要求给出要搜索的区间，设为(xl,xr)。那么两个黄金分割点就是

其中：

黄金分割率： 

以下有时写成了xr有时写成了xu，请把xr,xu看成一个点。

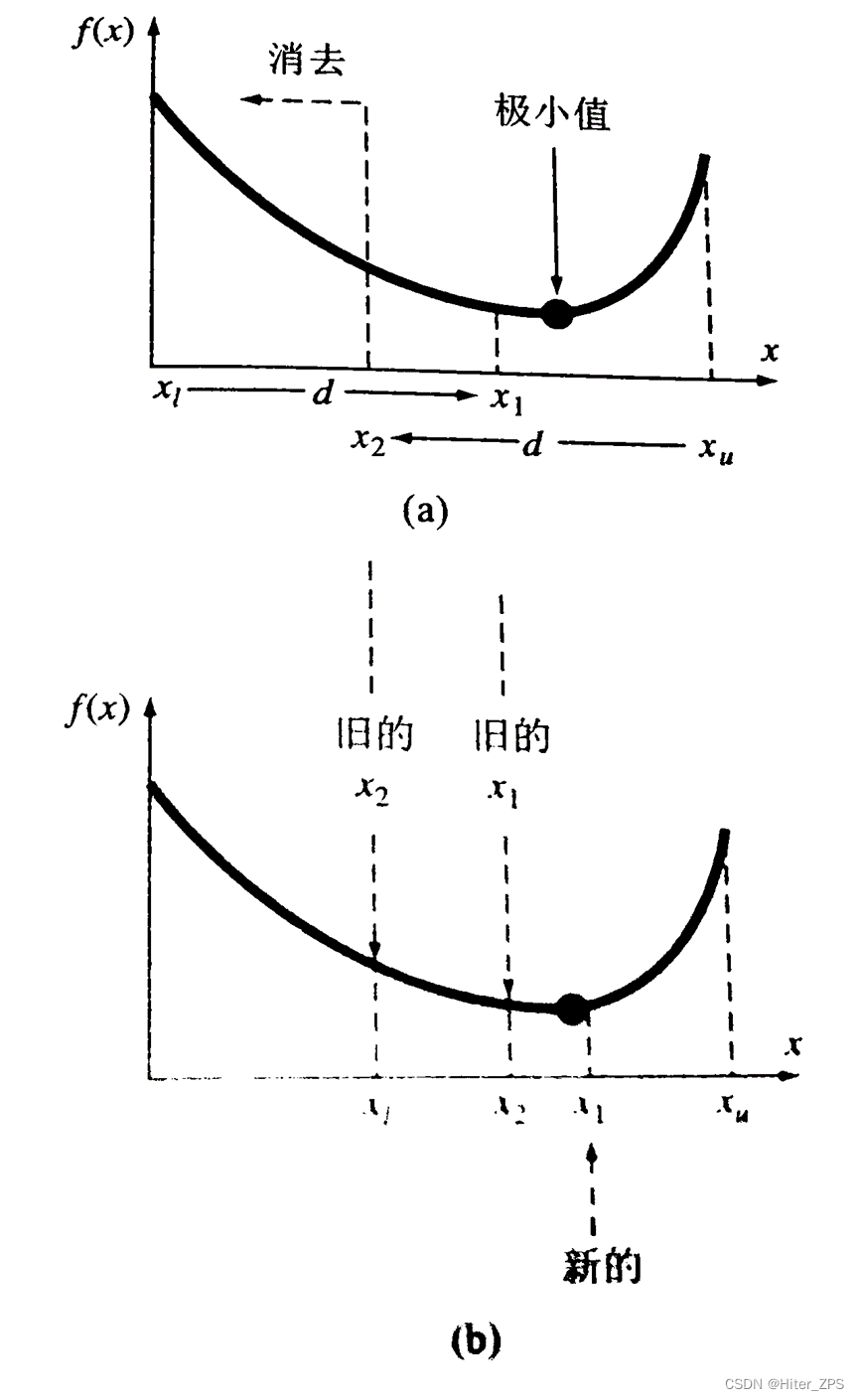
缩小区间：判断f1=f(x1)与f2=f(x2)的大小。

• 若f1<f2,则x1是局部极小值，xl~x2这一段就可以抛弃了，简单更新一下迭代值：xu为上界不变；由于（xl,x2）的抛弃，xl需要更新：xl=x2；这时候黄金分割法的优点就体现出来了，因为唯有黄金分割，才能使x1仍为下一个区间的一个黄金分割点，且为左黄金分割点，这样直接令x2=x1就完成了x2的更新；最后求解出新区间的右黄金分割点，令其为x1，就完成了迭代.

• 若f1>f2,则x2是局部极小值，x1~xu这一段就可以抛弃了，简单更新一下迭代值：xl为下界不变；xu需要更新：xu=x1；x2仍为下一个区间的一个黄金分割点，且为右黄金分割点，这样直接令x1=x2就完成了x1的更新；最后求解出新区间的左黄金分割点，令其为x2，完成迭代.

终止条件：如果最优点在x1处，则最终极小值在（x2,x1,xr）区间内

估计值最大可能距离为max(x1-x2,xr-x1)

通过计算：xr-x1=(2-)（xr-xl）=0.3820(xr-xl)>x1-x2=(2-3)（xr-xl）=0.2361(xr-xl).

故取

为终止迭代准则。

 代码实现

function [x,fx,ea,iter] = goldmin(f,xl,xr,es,maxit)
%goldmin:用黄金分割法求解函数极小值
%%输入:
%f=将要解的函数方程
%xl=（x_left），xl=（x_right）搜索区间
%es=允许的容差
%maxit = 允许的最大迭代次数
%%输出：
%x=所求极小值点
%fx=所求极小值
%ea=相对误差（ea<=es时即可输出）
%iter=迭代次数
if nargin<3,error('最少需要输入三个参数——函数和搜索区间'), end
%当输入的参数少于3个时，即函数和搜索区间没有齐全时，报错！
if nargin<4 || isempty(es),es=0.0001;end
%当输入的参数少于4个时（没有输入容差），默认为0.0001
if nargin<5 || isempty(maxit),maxit=50;end
%当输入的参数少于5个时（没有输入最大迭代次数），默认为50次
phi=(1+sqrt(5))/2;    %黄金分割数
iter=0;
d=(phi-1)*(xr-xl);
x1=xl+d;x2=xr-d;    %xl和xr之间的两个黄金分割点
f1=f(x1);f2=f(x2);
while(1)
    xint=xr-xl;
    if f1 < f2
        xopt=x1;    %x1是当前迭代的极小值点，用xopt表示
        xl=x2;    %舍弃掉xl~x2这一段区间，令x2为新的xl，缩小区间
        x2=x1;    %由黄金分割的性质，x1恰在新区间的左黄金分割点（令其为x2）上
        f2=f1;    
        x1=xl + (phi - 1)*(xr-xl); f1=f(x1);    %更新迭代值
    else
        xopt=x2; xr=x1; x1=x2; f1=f2;
        x2=xr - (phi - 1)*(xr-xl); f2=f(x2);
    end
    iter = iter + 1;
    if xopt~=0,ea=(2-phi)*abs(xint/xopt) ;end
    if ea <= es || iter>=maxit,break,end
end
x=xopt;fx=f(xopt);
end

问题求解

问题：

用黄金分割求如下函数极小值

 

 搜索区间为（0,4）。

f=@(x) (x^2)/10-2*sin(x);
[x,fx,ea,iter] = goldmin(f,0,4,0.0001,20)

结果:

>> goldmin_test
x =
    1.4275
fx =
   -1.7757
ea =
   1.1448e-04
iter =
    20

声明：文章来源于笔者学习【美】Steven C. CHapra所著，林赐译 《工程于科学数值方法的MATLAB实现》（第4版）的笔记，如有谬误或想深入了解，请翻阅原书。