MATLAB数值分析学习笔记：多项式拟合

在很多情况下，我们需要估计精确值之间的可能取值，常用的方法是多项式插值法。多项式插值法的原理是n个数据点可以确定n-1次多项式：例如三点确定一条抛物线。

工程上常用的多项式插值的方法有两种：牛顿插值法和拉格朗日插值法。

牛顿插值法

牛顿插值多项式的一般形式如下

从常系数到高阶过渡地求出系数bn，可以得到如下结果：

其中方括号代表有限均差。例如

 

均差表

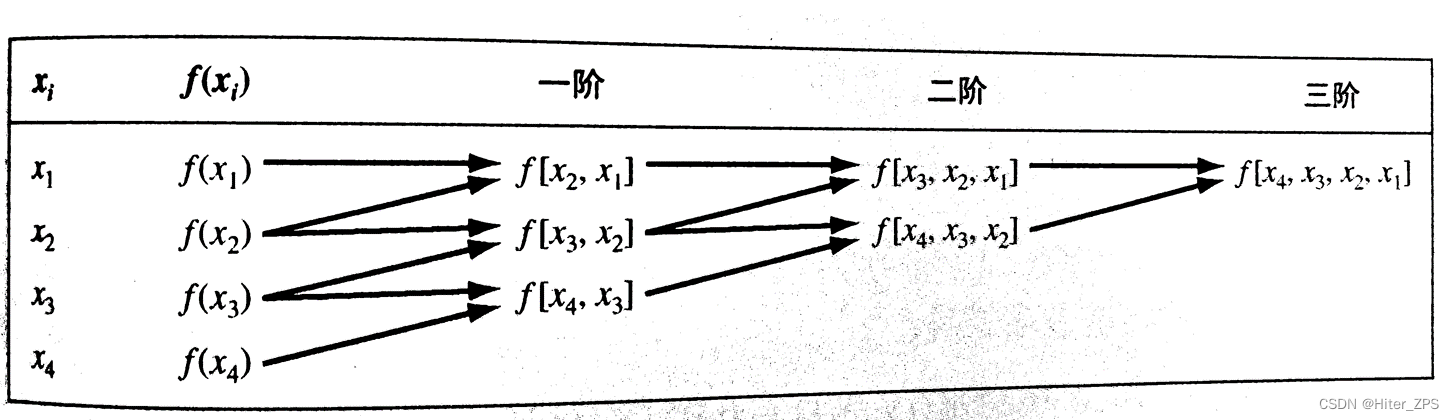
 代码实现

function yint = Newtint(x,y,xx)
%Newtint: Newton interpolating polynomial
%% 说明：使用n-1次多项式来进行插值
%
%输入：
% x=自变量
% y=因变量
% xx=需要被计算的自变量
% 输出：
%yint=需要计算的自变量对应的因变量值（插值多项式中）
%% 牛顿插值法计算多项式系数
n=length(x);
if length(y)~=n, error("自变量和因变量数组长度必须相同"); end 
b=zeros(n,n);
b(:,1)=y(:);
for j=2:n
    for i=1:n-j-1
        b(i,j)=(b(i+1,j-1)-b(i,j-1))/(x(i+j-1)-x(i)); %反复计算有限均差，得到系数
    end
end
xt=1;
%% 计算xx的因变量
yint=b(1,1);
for j=1:n-1
    xt=xt.*(xx-x(j));
    yint=yint+b(1,j+1)*xt;
end

 问题求解

例：作出下面测试数据的牛顿插值多项式图像，与原数据点放在一张图上并作比较

测试数据

x	0	1.8	5	6	8.2	9.2	12
y	26	16.415	5.3	3.5	2.015	2.54	8

解：

x=[0 1.8 5 6 8.2 9.2 12];
y=[26 16.415 5.3 3.5 2.015 2.54 8]
xx=0:0.1:12;
yy = Newtint(x,y,xx)
plot(x,y,'o')
hold on
plot(xx,yy)

得到图像如下，发现x=12处估计误差较大 

 拉格朗日插值法

将线性插值多项式看成由直线相连两个点的加权平均，则可以写为

第一个加权系数可以是x1出等于1、在x2出等于0的直线：

同理，第二个系数为

以此类推，可以得到拉格朗日插值多项式的一般形式：

其中拉格朗日系数为

代码实现

function yint = Lagrangeint(x,y,xx)
%Lagrangeint: Lagrange interpolating polynomial
%% 说明：使用n-1次多项式来进行插值
%
%输入：
% x=自变量
% y=因变量
% xx=需要被计算的自变量
% 输出：
%yint=需要计算的自变量对应的因变量值（插值多项式中）
%% 拉格朗日插值法计算多项式系数
n=length(x);
if length(y)~=n, error("自变量和因变量数组长度必须相同"); end 
s=0;
for i=1:n
    product = y(i);
    for j=1:n
        if i~=j
            product = product.*(xx-x(j))/(x(i)-x(j));
        end
    end
    s=s+product;
yint=s;   
end

 上例求解

x=[0 1.8 5 6 8.2 9.2 12];
y=[26 16.415 5.3 3.5 2.015 2.54 8]
xx=0:0.1:13;
yy = Lagrangeint(x,y,xx)
plot(x,y,'o')
hold on
plot(xx,yy)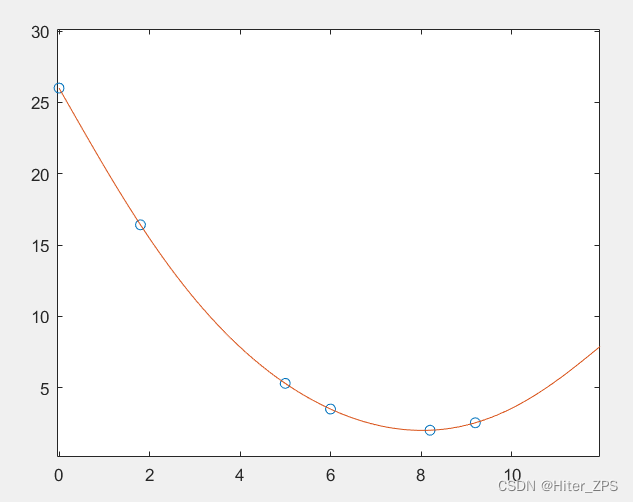

 内置函数

MATLAB中用于多项式插值的函数主要有polyfit和polyval

其中polyfit用于实现多项式回归，具体语法如下

p = polyfit(x,y,n)
[p,S] = polyfit(x,y,n)
[p,S,mu] = polyfit(x,y,n)

polyval用于多项式插值

y = polyval(p,x)
[y,delta] = polyval(p,x,S)
y = polyval(p,x,[],mu)
[y,delta] = polyval(p,x,S,mu)

应用起来很简单，用上例举例

测试数据

x	0	1.8	5	6	8.2	9.2	12
y	26	16.415	5.3	3.5	2.015	2.54	8

x=[0 1.8 5 6 8.2 9.2 12];
y=[26 16.415 5.3 3.5 2.015 2.54 8];
xx=0:0.1:12
p=polyfit(x,y,4);
yy=polyval(p,xx);
plot(x,y,'o')
hold on
plot(xx,yy)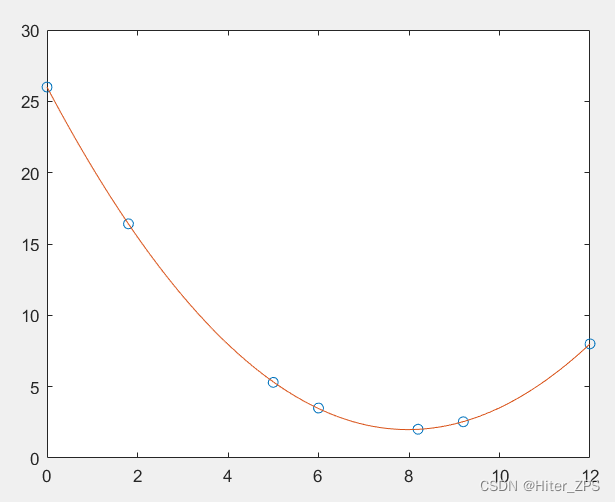

Remark: 

•  横坐标不等距通常会引起多项式插值的振荡
• 高次多项式插值的风险（Runge函数）

 

        对于下面的Runge函数，发现随着多项式次数增加。插值多项式与原曲线误差越来越大，下面分别取5个和11个点，进行4次和10次多项式拟合

x1=linspace(-1,1,5);%四次插值
y1=1./(1+25*x1.^2);
x2=linspace(-1,1,11);%十次插值
y2=1./(1+25*x2.^2);

xx=linspace(-1,1);
yi=1./(1+25*xx.^2);
p1=polyfit(x1,y1,4);%四次插值
y_1=polyval(p1,xx);
p2=polyfit(x2,y2,10);%十次插值
y_2=polyval(p2,xx);
pl1=plot(x1,y1,'o',xx,y_1,'b',xx,yi,'--',xx,y_2)
hold on 
pl2=plot(x2,y2,'*',xx,y_2,'k')
legend([pl1(3),pl1(2),pl2(2)],{'原始曲线','四次插值','十次插值'})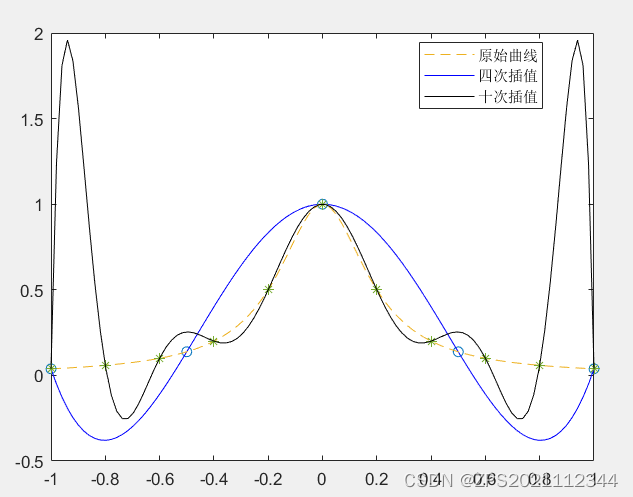

 可以发现，多项式插值不是次数越高越好，边缘可能会出现振荡。

声明：文章来源于笔者学习【美】Steven C. CHapra所著，林赐译 《工程与科学数值方法的MATLAB实现》（第4版）的笔记，如有谬误或想深入了解，请翻阅原书。