最优二叉搜索树

一只蒟蒻ovo

于 2024-04-30 16:26:01 发布

阅读量1k

点赞数 16

文章标签：数据结构动态规划算法

本文链接：https://blog.csdn.net/Zhang_Qin123/article/details/138322937

版权

一、二叉搜索树（二叉查找树）

所有根节点大于左子树的节点，小于右子树的节点的二叉树

满足以下性质：

1.如果左子树不为空，则左子树上的所有节点都小于根节点

2.如果右子树不为空，则右子树上的所有节点都大于根节点

3. 左右子树也为二叉搜索树

二、最优二叉搜索树

给定一个 n 个关键字的已排序的序列K=<k1，k2，k3......kn> （k1<k2<k3....<kn），对于每个关键字 ki ，都有一个概率 pi 表示其搜索频率，根据 ki 和 pi 构建一个二叉搜索树T，每个ki 对应树中一个节点，若搜索对象 x 等于某个 ki ，则可以在树T中找到该节点 ki 。

若 x<ki 或者 x>kn 或者 ki < x < ki+1 (1≤i<n)，则在T中搜索失败，此时引入外部节点 d0，d1，d2，.... dn，用来表示不在序列K中的值，称为伪节点，每个di 代表一个区间，即 d0 表示所有小于 k1 的值，dn 表示所有大于 kn 的值，对于剩下的 di 则表示在 ki 和 ki+1 之间的值，同时每个 di 也有一个概率 qi 表示搜索对象 x 落入区间 di 的概率。

将伪节点插入二叉搜索树中（ n=5 时），有多种形式

对于最优二叉搜索树，不同树的形式会产生不同的平均检索时间，求一颗平均比较次数最少的二叉搜索树。

平均检索时间：即检索遍历树中每个节点（K D序列）的时间期望

对于节点集　S＝< k1,k2,,,kn,d0,d1,,,,dn> 和概率分布 P=<p1,p2,,,,pn,q0,q1,,,,,qn>

规定树根的深度为 0 则节点 xi 在树中的深度为 depth(xi) i=0~n 空隙 dj 的深度为 depth(dj) j=0~n

平均比较次数公式（期望）

$m(T)=\sum_{i=1}^{n} p_{i}*(1+depth[k_{i}])+\sum_{j=0}^{n} q_{j}*depth(d_{j})$

公式理解：对于搜寻节点 ki ，从根节点到该节点需要 ( 1+depth[ki] ) 的步骤（包括根节点），对于搜寻空隙 di，则只需要(depth[di])的步骤（搜寻到 di 的父节点即可）

三、最优二叉搜索树算法（动态规划）

1.分析子问题（i，j）

找到含有节点 S=<ki,ki+1,,,kj,di-1,di,,,,dj> 概率分布P=<pi,pi+1,,,pj,qi-1,qi,,,qj> 的二叉搜索树

建立关系：以 ky 作为树的根，树被划为三部分

左子树：节点S [ i , y-1 ]，对应 P [ i , y-1 ]

根： ky

右子树：节点 S [ y+1 , j ]，对应 P [ y+1 , j ]

m[i,j]表示从节点 ki ~ kj 的最优二叉搜索树的平均比较次数（期望），则与（ky为当前树的根） m[i,y-1] m[y+1,j] 有递推关系：

$m[i,j]=min(m[i,y-1]+m[y+1,j]+w(i,j)) \, \, \, \, \, \, \, \, \, \, \, \, i\leq y\leq j$

$m[i,i-1]=q_{i-1} \, \, \, \, \, \, \, \, \, \, \, i=1,2,,,n$ (此时子树只有伪节点代价为 q[i-1])

1.m[i,y-1] 表示从节点 ki ~ ky-1 的最优二叉搜索树的平均比较次数

2.m[y+1,j] 表示从节点 ky+1 ~ kj 的最优二叉搜索树的平均比较次数

3. w(i,j) 对于给定的搜索数据 x，先要与 ky (根) 进行比较后才可以进入其左右子树查询，需要将 ky 与左右子树链接起来，子树的每个节点深度均增加1，所以比较次数需要加1，即 w(i,j)是由增加的左子树的比较次数，右子树的比较次数，和根的比较次数之和

$w(i,j)=w(i,k-1)+w(k+1,j)+1*q_{k}$

$w(i,j)=\sum_{a=i}^{j}p_{a}+\sum_{b=i-1}^{j}q_{b}$

$w(i,j)=w(i,j-1)+p_{j}+q_{j}$

2.推广至原问题，求最优二叉搜索树

以 1，2，3，4 这四个节点为例，分别以这四个节点作为根节点计算。

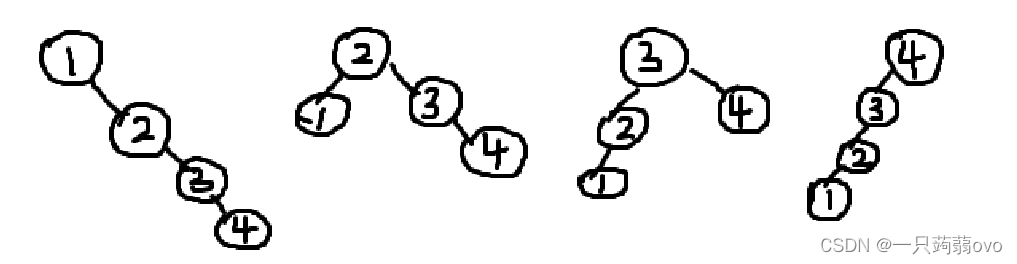
则此时计算出最优二叉搜索树从下面四个结果中取最小。

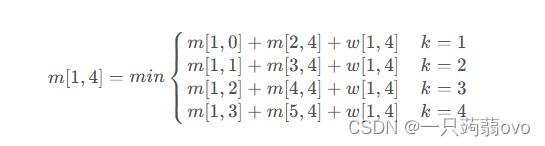
代码思想：

这里可以得出结论：ｍ［ｉ，ｊ］的计算是根据树中节点的个数判断的，首先需要一个循环记录节点的个数N，通过循环记录出起始节点ｉ，同时得出末尾节点ｊ＝ｉ＋Ｎ－１，再循环ｉ～ｊ之间的根节点ｋ，即可得出结论．因此时间复杂度为　 $O(n^{3})$

3.寻找最优方案

和之前的切割问题一样，只需要记录下当 m [ i , j ] 在最小时取到的根节点 k 即可 x [ i , j ] = k

在寻找最优方案时，从 x[1,n] 出发，通过递归将其分成 i~x[1,n]-1 与 x[1,n]+1~n，再依次类推,得出最优方案.

代码：

#include<stdio.h>
#include<iostream>
using namespace std;
int n,k[10001],d[10001],s[1001][1001];
double p[10001],q[10001];
double m[1001][1001],w[1001][1001];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)  scanf("%lf",&p[i]);
	for(int i=0;i<=n;i++)  scanf("%lf",&q[i]);
	for(int i=1;i<=n+1;i++)  
	{
		m[i][i-1]=q[i-1];  // 初始化默认伪节点 
		w[i][i-1]=q[i-1];
	}
	for(int l=1;l<=n;l++)
	for(int i=1;i<=n-l+1;i++)
	{
		int j=i+l-1;
		m[i][j]=100001;
		w[i][j]=w[i][j-1]+p[j]+q[j];  // W 的递推公式 
		for(int k=i;k<=j;k++)
		{
			if(m[i][k-1]+m[k+1][j]+w[i][j]<m[i][j])
			{
				s[i][j]=k;
				m[i][j]=m[i][k-1]+m[k+1][j]+w[i][j];
			}
		}
	}
	printf("%lf",m[1][n]);
}