浅谈神经网络归一化(输入归一化，BatchNorm和LayerNorm）

工大CV吴彦祖

已于 2025-03-23 20:21:25 修改

阅读量7.4k

点赞数 31

分类专栏： PytorchCV 文章标签：人工智能算法

于 2024-02-17 02:41:45 首次发布

本文链接：https://blog.csdn.net/Zssss12/article/details/136110017

版权

PytorchCV 专栏收录该内容

14 篇文章

订阅专栏

以前常看到许多著名的模型中(Transformer,SwinTransformer...)都存在着归一化操作,当时只道是寻常，了解了大概功能和其存在的意义之后就没再深研究，最近自己上代码打算着手实战，相对这个操作进行一个概要的梳理，重点在与原理与应用。

为什么要归一化？

大家在看论文时肯定都看到过归一化这个操作，那么为什么要进行归一化操作呢？GPT3.5返回的的答案是：“神经网络进行归一化是为了将输入数据的范围缩放到合理的区间，以便更好地进行训练和优化。归一化可以有助于提高模型的收敛速度，避免梯度消失或梯度爆炸问题，并增加模型的稳定性和泛化能力。”

为什么归一化可以更好的训练模型和优化呢？GPT回答的比较概括，具体来说，有以下几个方面的原因。

减少数值计算的复杂性：这点是最直接，最好理解的，在深度学习中，模型涉及大量的数值计算。如果输入数据的尺度很大，这些计算可能会涉及较大的数值范围，导致数值溢出或下溢的问题。通过数据缩放，可以将输入数据的范围缩小到较小的数值范围，有助于减少数值计算的复杂性和数值稳定性问题。
改善梯度下降：梯度下降是深度学习中常用的优化算法，通过沿着梯度的反方向来更新模型参数。当输入数据的尺度差异很大时，梯度下降的效果可能会受到影响，我们都知道，计算梯度时是基于链式求导法则计算梯度的，设损失函数为 $L\left ( w_1,...,w_n,b_1,...,b_m,... \right )$ ，它是所有被训练参数的函数，假设正在更新 $w_1$ ,那么链式求导公式也许可以写成这样 $\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial h}\frac{\partial h}{\partial g}\frac{\partial g}{\partial f}\frac{\partial f}{\partial w_1}$ ,其中 $f,g,h$ 是不同的函数，反正求 $w_1$ 梯度的最后一层偏导肯定是加权输入最近的激活函数算一个篇导数，再乘以该输入，以最广为人知的Sigmoid函数为例子 $Sigmoid(x)=\frac{1}{1+e^{-x}}$ 我们看下表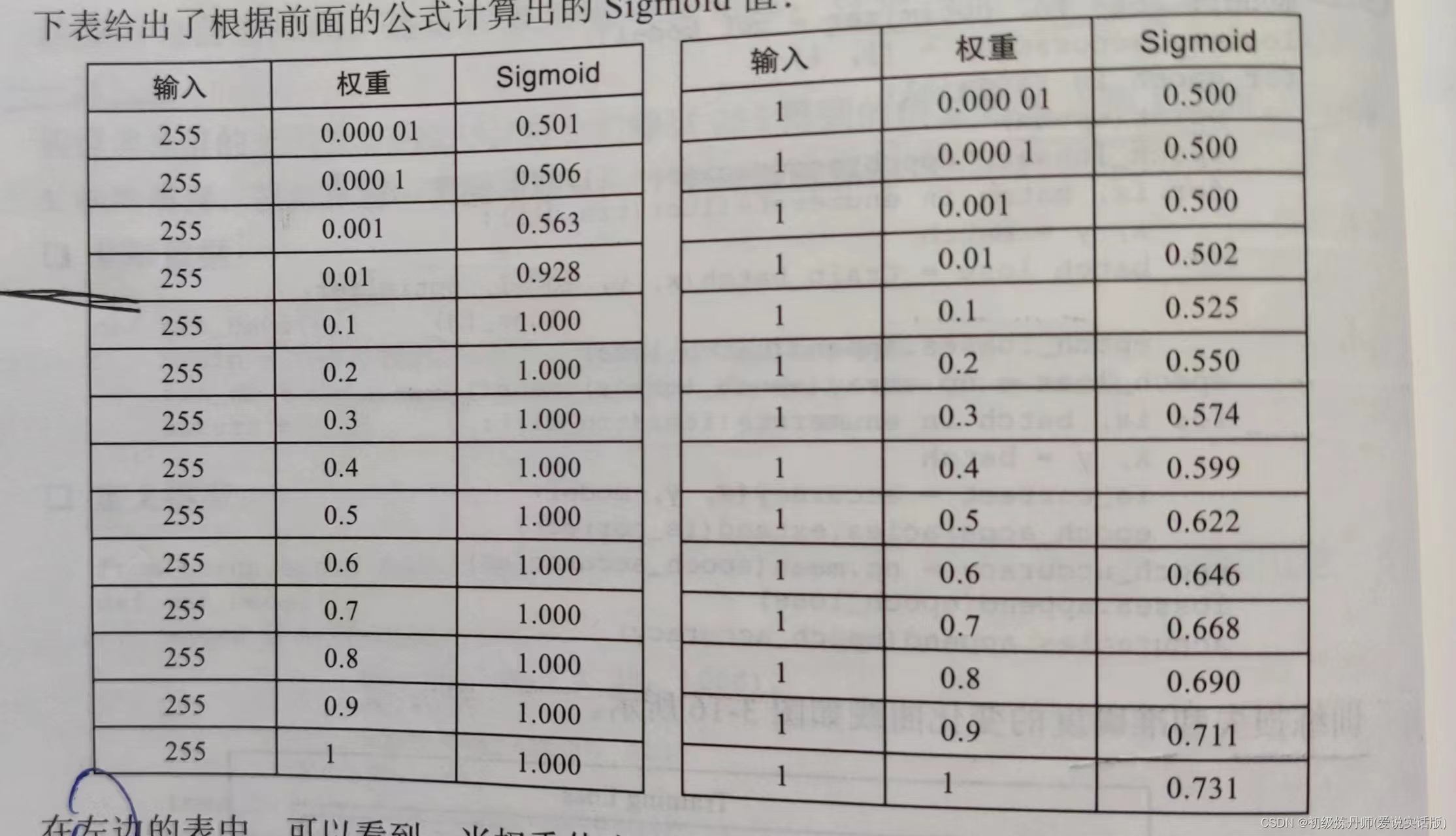，当输入是255时(RGB图像，的一个通道的一个像素点),当接收该输入的权重大于0.1是sigmoid的输出是不变的，这有什么影响？影响是单算链式求导的这一层偏导时，对权重的小幅度更改可能不会导致激活函数的输出有变化，那么由导数定义可知，这一层的导数为0！,又由于链式求导是相乘，这就会导致这个权重 $w_1$ 的梯度整体为0！它将不能更新，这个参数就学不明白了,同理输入过小的时候如下图，当权重小于0.2时sigmoid的输出不变，也会造成梯度消失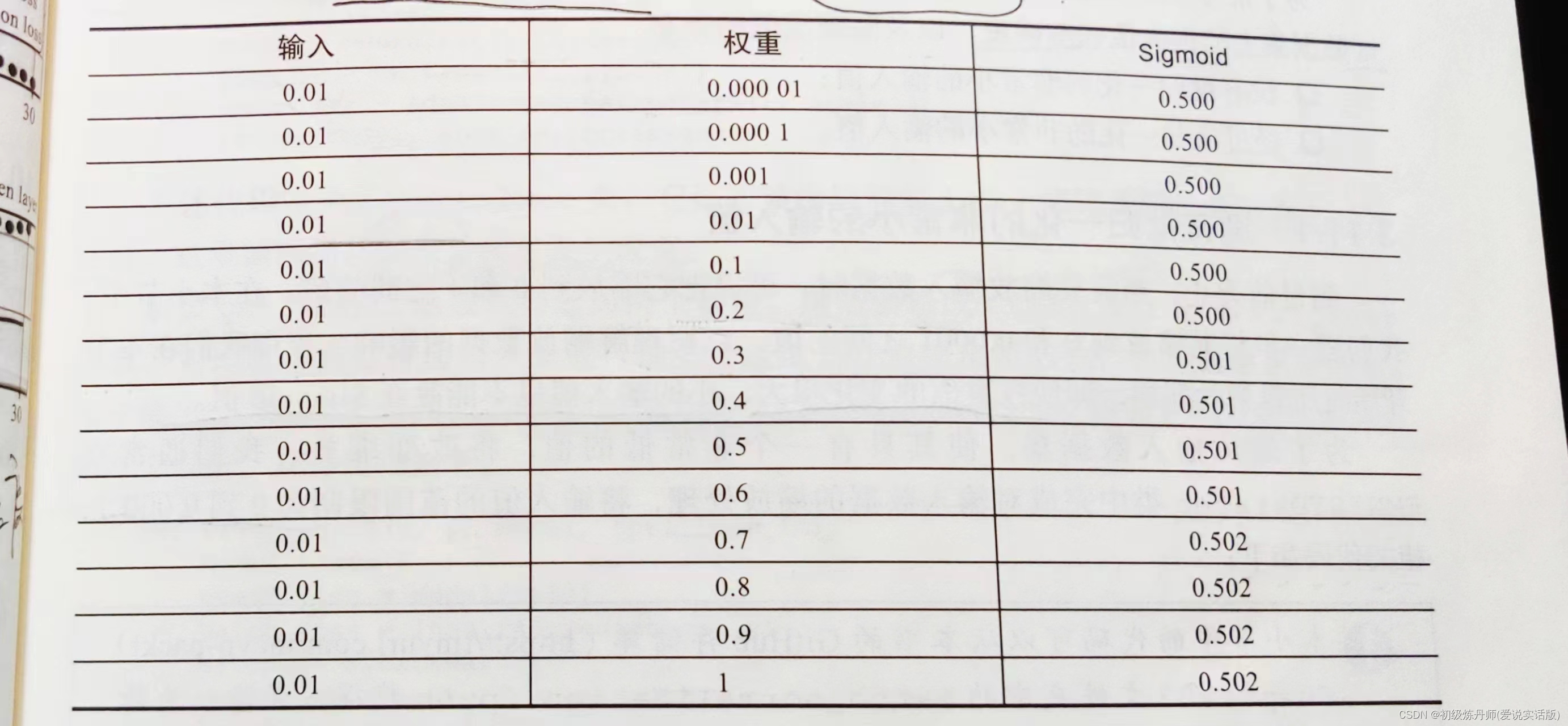但如果将输入归一化，原来[0,255]归一化到[0,1]如右表，权重的变化就会引起激活函数的变化，模型就可训练了。
统一量纲：设想一种情况，我用多模态数据作为输入，每个输入的量纲都不一样，有的是几十几百，有的是零点几的小数，而我所有权重偏置的初始都是由正态分布随机初始化的，那么这些随机初始化的数据差异也不会偏差太多，如果我们对很大的输入和对很小的输入都用相同的权重的话，那么大量纲的输入将对神经元的兴奋起主导作用，大量纲的输入就比小量纲的输入更有用吗？显然不是的，我们只想知道，大量纲输入内部的相对关系，和小量纲输入内部的相对关系，所以我们理应进行归一化操作。
加快收敛速度：这里跟统一量纲一同理解，假如我不进行归一化，那么模型自己就要去学这种量纲内部的相对关系，这就会导致模型帮你归一化，大量纲输入的权重小，小量纲输入的权重大，这就产生了一个问题，权重的量纲不统一，如果我们采用SGD优化算法，计算梯度后乘以相同的学习率，小量纲的权重变一点（对应大输入）对损失的影响很大，他的梯度很大，但是小量纲的权重应该慢调，大量纲的权重变一点（对应小输入）对损失的影响没那么大，他的梯度也没那么大，但是大量纲的权重应该快点调，这就很难统一一个合理的学习率，如果为了保险起见把学习率调的过小就会使一些参数先收敛一些参数后收敛，为了同时收敛就要训练更多的epoch，然而先收敛的参数又可能会过拟合，难以学到合理参数，(以上只是定性分析，理解意思即可），所以我们要进行归一化操作，这样可以使网络参数也间接归一化，方便学习率的选择（可以选择更大的学习率）和加速整体模型的收敛(即使用Adam优化器的动态学习率也不能不做归一化操作),使训练过程更加稳定
起到一定正则化的效果：归一化可以起到一定的正则化效果。归一化是将输入数据的特征值缩放到一个较小的范围内，使其具有相似的尺度。这有助于减少特征之间的差异，提高模型的稳定性和泛化能力，从而减少过拟合的风险。

在哪进行归一化？

归一化通常在以下两个位置进行：

输入特征归一化：将输入的特征数据进行归一化处理。这样做可以确保不同特征之间具有相似的尺度，避免某些特征对模型训练的影响过大。通常使用的方法有标准化（将特征缩放为均值为0，方差为1），最小-最大缩放（将特征缩放到指定的最小值和最大值之间），以及其他归一化方法。
每层特征输入到激活函数之前：关于很小或很大的输入值，也可能遇到下面这种情形：某个隐藏层的节点可能会产生一个很小的数值或一个很大的数值，此时将隐藏层权重连接到下一层就会导致之前遇到的同样的问题。（及此时隐藏层可以被视为输入层）在这种情况下，可以使用批归一化方法解决这个问题，因为这种方法对每个节点上的值进行了归一化处理，就相对输入值进行缩放处理一样。

归一化方法

BatchNorm

论文出处[1502.03167] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (arxiv.org)
batchnorm是一个非常经典的buildingblock(方便加速训练，方便结构化,训练效率更高)，它变成了一个深度网络的标配(使网络训练快，收敛快，整个网络更稳健，部分解决过拟合）
我们之前只对输入进行norm，现在我们对每一层进行norm
norm的意思是0均值，1标准差，还有γ和β作为可学习的参数
对批次(batch)内特征进行归一化(不是对单一样本进行归一化，对比于：LayerNorm)
不改变数据shape:BatchNorm1d:N*d——>N*d(fearure)

BatchNorm2d:N*C*H*W——>N*C*H*W(RGB image)

BatchNorm3d:N*C*d*H*W——>N*C*d*H*W(Deep image)

公式
具体思想1d；2d；3d：(这篇讲的很清楚了）nn.BatchNorm讲解，nn.BatchNorm1d, nn.BatchNorm2d代码演示-CSDN博客
官方文档：BatchNorm1d — PyTorch 2.2 documentation

BatchNorm2d — PyTorch 2.2 documentation

BatchNorm3d — PyTorch 2.2 documentation

Layernorm

Layer normalization (LayerNorm)是一种归一化技术，用于在深度学习模型中对输入或激活进行归一化。它的设计灵感来自于Batch Normalization（BatchNorm），但与BatchNorm不同，LayerNorm是在单个样本或单个样本的特征维度上进行归一化，而不是在整个批次上进行归一化。
LayerNorm的主要目的是减小神经网络中的内部协变量偏移（Internal Covariate Shift），即在网络的不同层之间输入分布的变化。它通过对每个样本或特征维度进行归一化，使得它们的均值为0，方差为1，从而使得网络的学习更加稳定和可靠。
LayerNorm的计算过程如下：

对于每个样本，计算其在特征维度上的均值和方差。
使用计算得到的均值和方差对样本进行归一化。
使用可学习的参数（缩放因子和偏移量）对归一化的结果进行缩放和平移。

公式：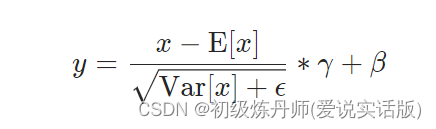

官方文档：LayerNorm — PyTorch 2.2 documentation

Batchnorm和layernorm的差异

1. 归一化范围：
- LayerNorm：它对每个样本进行单独归一化，即独立地对每个样本在所有特征或通道上进行归一化。它为每个单独的样本计算均值和方差。
- BatchNorm：它对每个特征或通道在一个批次的样本中进行归一化。它为每个特征或通道在批次中计算均值和方差。

2. 训练和推理行为：
- LayerNorm：在训练和推理过程中表现一致。归一化统计量是根据每个样本的输入数据单独计算的，适用于样本数量较小或需要在不同批次之间保持一致统计量的任务。
- BatchNorm：在训练过程中，它使用批次统计量计算归一化统计量。然而，在推理过程中，统计量是固定的，并根据训练过程中收集的批次统计量的移动平均值来计算。BatchNorm在推理过程中引入了额外的复杂性，因为它依赖于批次统计量，但它可以提供正则化的好处。

3. 适用范围：
- LayerNorm：常用于具有时间序列依赖关系的循环神经网络（RNN），它有助于在时间步骤上对RNN的隐藏状态进行归一化。
- BatchNorm：广泛应用于具有空间依赖关系的卷积神经网络（CNN），它对空间维度（如高度和宽度）上的激活进行归一化，有助于减少内部协变量偏移。

对此作一个刚详细的解读：

BatchNorm更适合计算机视觉（CV）任务，而LayerNorm更适合自然语言处理（NLP）任务，这主要与两者的数据结构、任务特点以及归一化操作的性质有关，以下是具体原因：

BatchNorm更适合CV任务的原因

• 数据结构特点：CV任务中，输入数据通常是图像，其形状为（batch_size,channels,height,width），即批量大小×通道数×高度×宽度。BatchNorm是对一个batch中同一通道的所有特征进行归一化，这样可以将不同图像的同一通道特征（如颜色通道）调整到相似的分布。例如，对于RGB图像，BatchNorm可以分别对红色、绿色和蓝色通道的特征进行归一化，使得不同图像的同一颜色通道特征具有可比性。

• 任务需求：在CV任务中，图像的特征是客观存在的，例如纹理、颜色、形状等。BatchNorm通过归一化操作，可以保留不同图像的同一特征之间的相对关系，这对于模型学习图像的通用特征（如边缘检测、纹理识别等）非常有帮助。

• 训练稳定性与效率：BatchNorm能够有效减少模型训练对初始化的依赖，提高梯度在网络中的流动，从而加快模型的收敛速度。在CV任务中，模型通常需要处理大量的图像数据，BatchNorm可以帮助模型更稳定地训练，尤其是在使用较大的学习率时。

LayerNorm更适合NLP任务的原因

• 数据结构特点：NLP任务中，输入数据通常是文本序列，其形状为（batch_size,seq_len,embedding_dim），即批量大小×序列长度×嵌入维度。每个句子的长度不一定相同，对于缺少的内容可能会用其他值填充，同一个词在不同的句子中可能有不同的含义，因此不能简单地将不同句子中相同位置的词进行比较，即BatchNorm不适用。

• 任务需求：在NLP任务中，语义信息是由上下文决定的。LayerNorm是对每个样本的所有特征（即一个句子中的所有词向量）进行归一化，可以保持同一句子中词向量之间的相对关系，这对于模型理解上下文语义非常重要。

• 独立于批次大小：LayerNorm不依赖于批次大小，这使得它在处理小批次数据时表现更好。在NLP任务中，由于文本序列长度可能变化较大，有时需要使用较小的批次大小以避免内存问题。LayerNorm在这种情况下仍然可以有效地工作。

• 模型结构适应性：Transformer类模型是NLP任务中常用的架构，而LayerNorm与Transformer的结构非常契合。LayerNorm可以对每个token的特征向量进行归一化，这有助于模型学习更稳定的语义表示，并且不会破坏token特征向量之间的相对角度关系，从而更好地支持基于相似度的计算。

4. 参数化：
- LayerNorm：它为每个特征或通道引入可训练参数，例如比例和偏移参数，允许网络独立地学习每个单独样本的最佳比例和偏移。
- BatchNorm：它与LayerNorm类似，为每个特征或通道引入可训练参数，但还包括用于推理过程中的批次统计量（均值和方差）的额外参数。

总之，LayerNorm在每个样本上进行归一化，而BatchNorm在批次上进行归一化。LayerNorm常用于RNN，而BatchNorm广泛用于CNN。LayerNorm和BatchNorm的训练和推理行为也不同，LayerNorm始终保持一致的行为，而BatchNorm在推理过程中依赖于批次统计量。这篇文章说的很好：

BatchNorm和LayerNorm——通俗易懂的理解_layernorm和batchnorm-CSDN博客

【机器学习】LayerNorm & BatchNorm的作用以及区别_layernorm的作用-CSDN博客