Change-making problem(换零钱问题)
问题的描述如下:
how can a given amount of money be made with the least number of coins of given denominations?
这是一个knapsack type problem(背包问题), and has applications wider than just currency.
该问题的数学语言描述如下:
Given a set of integer coin values {w1, w2, ..., wn} where w1 = 1 and wj < wj+1 for 1 ≤ j ≤ n − 1, and a positive integer W, find a set of non-negative integers {x1, x2, ..., xn} (对应需要的各个面值硬币的个数)which minimize
subject to
-

-
- 该问题的求解办法如下有三种办法, 下面一一介绍。
- (1)动态规划(dynamic programming)
- (2)贪婪算法(greedy algorithm)
- (3)线性规划(Linear programming)
-
- 方法一: 动态规划解决
- 一个问题要能使用动态规划解决, 该问题必须满足具有最优子结构 和 递归的原则。 下面我们来看看。
- (1)最优解(optimal solution)的结构(structure)
-
假如我们具有的硬币的不同的面值为
, 假设我们每一种面值的硬币的个数是无穷大。 现在我们想要用这个硬币集合去兑换价值为 n 的纸币。 现在假设我们兑换成了一堆等值的硬币(最优的结果, 注意最优的兑换结果不是唯一的), 下在我们将这堆硬币任意分成两堆, 一对的价值是b, 另外一堆的价值是n - b. 例如下面:
-
-
- 不难看出我们有如下的claim 成立:
-
- 证明略(Hint: proof by contradiction)
- 根据上述的声明, 我们有如下的结论:
-
-
- (2)递归结构
-
- 注意, 在对p 分钱进行兑换的时候, 对于最佳解(optimal solution),
-
- 递归式子如下:
-
-
- 接下来, 该算法的伪代码如下:
-
-
- 我们还有如下声明:
-
-
- C++ 程序如下:
-
#include <iostream> #include <climits> using namespace std; void makeChange(int d[], int k, int n) { const int Size = n + 1; int C[Size]; int S[Size]; C[0] = 0; S[0] = 0; int coin; int Min; for (int p = 1; p <= n; p++) { Min = INT_MAX; for (int i = 1; i <= k; i++) { if (d[i] <= p) { if (1 + C[p - d[i]] < Min) { Min = 1 + C[p - d[i]]; coin = i; } } } C[p] = Min; S[p] = coin; } for (int i = 0; i < Size; i++) { cout << C[i] << " "; } cout << endl; for (int i = 0; i < Size; i++) { cout << S[i] << " "; } cout << endl; while(n > 0) { cout << d[S[n]] << " " << endl; n -= d[S[n]]; } } int main() { int denomi[] = {0, 1, 3, 4}; int k = 4; int note = 0; cout << "please input a note in cents: "; cin >> note; makeChange(denomi, k, note); return 0; }
运行结果为: -
-
- 算法复杂度分析:
-
-
- (2)贪心算法
- 动态规划在解决这类问题的时候可能overkill, 我们需要更快的, 更简洁的算法, 那么我们常常选择贪婪算法来解决这个问题。 但是贪婪算法也有缺陷, 就是不保证找到最优的解。 例如:
-
硬币面值1,10,25.找30分钱,最优解是3*10,而贪心的情况下产生的解是1*5+25。
- any way, 下面介绍贪心算法。 贪心算法的遵循的规则就是每一次都选取当前看起来的最优的策略。 例如, 在coin change problem中, 我们的测量就是优先选取“面值大的硬币”。
-
- 需要注意的是, 上述算法并不总是产生最优的解, 例如:
-
-
- 但是, 虽然贪心算法不保证找到的解是最优的, 但是当我们的输入满足一定的条件的时候, 得到的结果就是最优的!!!!!!!!!!!!
- 例如, 对于US currency, 总过的面值有25, 10, 5, 1, 即如下:
-
- 证明如下:
-
-
方法三 线性规划(略)
Integer Linear Programming is often a quick way to solve this kind of problem, but the time it will take to resolve the problem is not certain, and may be slow in some cases








 本文探讨了换零钱问题,即如何用最少数量的特定面值硬币凑出指定金额,这是一个典型的背包问题。通过数学描述和约束条件,文章揭示了解决这一问题的重要性及其在货币以外的广泛应用。
本文探讨了换零钱问题,即如何用最少数量的特定面值硬币凑出指定金额,这是一个典型的背包问题。通过数学描述和约束条件,文章揭示了解决这一问题的重要性及其在货币以外的广泛应用。
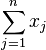





























 8435
8435

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








