数据结构 算法 时间复杂度 有序二叉树 平衡二叉树

Java的学习过程

类和对象（Java中最基本的部分，目前已经学完了） → 练习最基本的数据结构和算法 → Java基础的中阶（封装、继承、多态）→ 高阶（反射代理）

数据结构

数据结构就是研究数据在内存中如何进行高效存储。数据结构包括：数组+链表+树+...

以数组和链表举例

假设有一个无序数组，我们想要对其进行查询，如果知道要查询的数据的下标，我们就可以对其进行查询；也可以通过数据一个一个往后走进行查询，因为数组的数据是一个个紧挨着的连续的，所以我们对其查询的代价也是比较小的，会比较高效。

但是当我们想要删除数组里的一个数据时，我们不能凭空将想删除的数据从数组删除，因为数组是一块连续的内存空间，不能被分成两段。于是在数组中，要删除一个数，只能让后面的数依次向前进行覆盖，随后空出来的位置我们就将其置空。

插入也是同样的道理，将数据放在想要放的角标上，再将原本的数以及之后的数依次向后覆盖，因此对于一个数组内数据的删除和插入都是十分复杂的。

对于链表而言，如果想要删除一个数据，那就只需要让上一个数据指向下一个数据，中间的数据在内存中就没有作用了；而想要插入一个数的时候，只需要让新的数指向一个数，再让原本指向那个数的数指向要插入的数即可，所以链表的插入和删除是很方便快速的。

但是当我们想要查询链表中的一个数的时候，由于链表每个数据的地址是不连续的，在查询上付出的代价就特别高。

结论：如果我们的数据优先查询就选择数组，如果优先插入和删除就选择链表。

算法

算法就是解决问题的方法。

示例

以一个计算题举例：假如我们要计算 1+2+3+...+10000 的结果，我们可以怎么做？

方法一：使用for循环依次计算

public static void sum (int n){
    for(int i=0; i<n;  i++){
        sum = sum+i;
    }
}

方法二：使用等差数列公式计算

public static void sum (int n){
    sum=n*(1+n)/2;
}

由此可见，第一种也叫算法，第二种也叫算法，它们都是针对同一个问题的解决方法，区别只是计算的复杂度不同导致计算时间不同。方法一种要从1一直加到10000，进行10000次运算；而方法二只需要进行一次运算即可。所以方法一的计算复杂度更高，计算时间更长。

那么问题就来了，两种方法究竟谁更好谁更差呢？

时间复杂度

评判一个算法好坏一般从两个维度判断：时间复杂度和空间复杂度。

空间复杂度：反映当前这个算法所消耗的内存空间大小；

时间复杂度：反映当前这个算法数据的计算量。（最被看重的维度，评判算法好坏的标准也以该维度为主）

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < ...

如何计算算法时间复杂度

假设一个算法处理的数据总量是n（足够大），为了增删改查等目的，消耗计算次数y，存在：

y = an+b（a是系数，b是常数）假设n足够大的情况下，a和b失去了意义，y=n，时间复杂度也就是O(n)；

y = an^2+bn=c，假设n足够大的情况下，a和bn失去了意义，y=n^2，时间复杂度就是O(n^2)；

y = a，时间复杂度就是O(1)；

y = logn，时间复杂度就是O(logn)。

在上述例子中，方法一就是O(n)的时间复杂度，方法二就是O(1)的时间复杂度。

几个计算时间复杂度的题目

（1）以下算法的时间复杂度为：

void fun(int n){

    int i=1;

    while(i<=n)

        i=i*2;

}

分析：

第1轮 i=1=2^0

第2轮 i=2=2^1

第3轮 i=4=2^2

第4轮 i=8=2^3

第5轮 i=16=2^4

第y轮 i=2^(y-1) > n

由于时间复杂度并不严谨，可作简化近似式子

→ 2^y = n → y = log2 n

→O(log2 n)

（2）以下算法的时间复杂度为：

void fun(int n){

    int i=0;

    while(i*i*i<=n)

        i++;

}

分析：

第1轮 i=0 0=0^3

第2轮 i=1 1=1^3

第3轮 i=2 8=2^3

第4轮 i=3 27=3^3

第y轮 i=y-1 (y-1)^3>n

由于时间复杂度并不严谨，可作简化近似式子

→ y^3=n → y=3√n

→O(3√n)

（3）以下算法的时间复杂度为：

x=2;

while(x<n/2)

x=2*x;

分析：

第1轮 x = 2 = 2^1

第2轮 x = 2*2 = 2^2

第3轮 x = 2*2*2 = 2^3

第4轮 x = 2*2*2*2 = 2^4

第y轮 x = 2^y>n/2

由于时间复杂度并不严谨，可作简化近似式子

2^y = n → y = log2 n

→O(log2 n)

（4）以下算法的时间复杂度为：

int func(int n){

    int i=0, sum=0;

    while(sum<n)
    
        sum += ++i;

    return i;

}

分析：

第1轮 i=0 sum=0

第2轮 i=1 sum=0+1=1

第3轮 i=2 sum=0+1+2=3

第4轮 i=3 sum=0+1+2+3=6

第5轮 i=4 sum=0+1+2+3+4=10

第y轮 i=y sum=0+1+2+3+4+...+(y-1)= y*(0+(y-1))/2 >= n

由于时间复杂度并不严谨，可作简化近似式子

y^2=n → y= √n

→O(n^(1/2))

数据结构设计原理

假如有一个无序数组，要求对该无序数组进行查询，求查询的时间复杂度

当知道下标的时候，可以直接通过下标进行查询，此时时间复杂度是O(1)。但是大多数时候我们并不知道下标，于是需要对数组进行遍历，如果数组长度是n，此时需要查询n次，即无序数组的时间复杂度是O(n)

时间复杂度我们平时都是尽可能降低，那对于这个问题我们如何降低时间复杂度

        （1）将无序数组转变为有序数组；

        （2）通过折半查找法进行查询：

                ① 假设要查询的值叫做target，我们确定数组第一个位置（arr[0]）定义为left，数组的最后一个位置（arr[arr.length-1]）定义为right

                ② 我们定义一个变量mid = (left+right)/2

                ③ 我们将target与arr[mid]进行比较。

                        如果arr[mid]<target，则说明包括mid之后的所有数据都比target小，此时我们让right指到mid的位置，mid重新计算；

                        如果arr[mid]>target，则说明包括mid之后的所有数据都比target大，此时我们让right指到mid的位置，mid重新计算；

                        如果arr[mid]=target，则说明找到了要找的数，查找完成。

                ④ 重复③直到完成查找

对于该查找方式，我们消耗的时间复杂度是:

        分析：

        第1轮 n=(1/2)^0 *n

        第2轮 n=(1/2)^1 *n

        第3轮 n=(1/2)^2 *n

        第y轮 n=(1/2)^(y-1) *n

        由于时间复杂度并不严谨，可作简化近似式子

        (1/2)^y=n → y=log(1/2) n

        → O(log(1/2) n)

但是在该例子中，我们还需要考虑如何将数组从无序变为有序，以及改变数组的时间复杂度。将数组变为有序可以使用8大排序算法。

在8大排序算法中，快速排序法是最快的排序方法，时间复杂度是最低的，为O(nlogn)。

此时我们可以发现，即使是最快的快速排序法，它的时间复杂度与我们查找的时间复杂度加起来已经超过了遍历的时间复杂度O(n)，所以这样的方式肯定是行不通的。

有人提出一种算法，当我们想要将一个数插入一个数组的时候，用这个数n对数组的长度取余，并将n存放在这个数组里面上述余数的位置，后续查询的时候只需要将要查询的数target按照这个计算公式求出其角标即可，此时的时间复杂度是O(1)。

但是这样的算法同样存在问题，即当我们出现了相同余数的情况下无法将两个数放在同一个位置（这种现象叫做哈希碰撞），如果往前或者往后放一位的话就会占据其他数的位置，这种情况又应该怎么办呢？

有人提出可以使用多维数组的形式来存储这些数，当一个数组插入了足够的数之后，将这个数组禁用，并将数据存入新的数组，但是这种情况下，当多维数组同一个角标的位置都被占据之后又得开辟新的数组再将原来的存储进去，这样的做法十分复杂，同时单链长了以后也会变成O(n)，并且还会造成大量的空间浪费，因此也不可取。

同时有人就说可以使用链表的方式进行数据的插入，当需要占用同一个角标的时候将新的数存储在别的位置，并将原本的数指向这个数，形成一个链表。当单链上链表比较短的时候我们还可以认为这个时间复杂度为O(1)，这种方式被称为拉链法。

但是拉链法仅仅在链表比较短的时候时间复杂度是O(1)，当链表长了以后时间复杂度仍然是O(n)，为了解决这种方法，科学家就创造了树。

树

树分为二叉树和多叉树

在二叉树中比较有名的有：线索二叉树、完全二叉树、满二叉树、二叉排序树（有序二叉树）、平衡二叉树、红黑树（最优二叉树）、哈夫曼树。

有序二叉树

特点

在插入的过程中，左子树比父节点小，右子树比父节点大。

示例

对于一组数据 8 5 7 4 10 19 12 进行插入：

        第1次 8 直接插入即可，作为根节点；

        第2次 5 插入发现比8小，插入到8的左边；

        第3次 7 插入发现比8小但是比5大，插入到5的右边；

        第3次 4 插入发现比8小也比5小，插入到5的左边；

        第3次 10 插入发现比8大，插入到8的右边；

        第3次 9 插入发现比8大但是比10小，插入到1的左边；

        第3次 12 插入发现比8小也比10大，插入到10的左边。

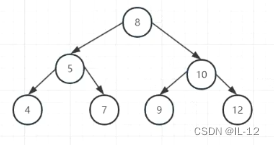
插入结果如图所示，该树相当于一个变相的折半查找法，其时间复杂度为O(log n)级别。

缺陷

有序二叉树的时间复杂度十分不稳定，当输入的数据排序越偏向与单链的时候，其时间复杂度越接近或者就是O(n)级别的时间复杂度。

平衡二叉树（二叉排序树的改进）

特点

在二叉排序树的基础上，要求左右子树高度差的绝对值不能超过1，一旦超过了1，立马进行旋转。

示例

对于一组数据 5 7 4 2 0 3 1 6 进行插入：

        第1次 5 直接插入即可；

        第2次 7 插入5的右边，此时5的左字树高度0，右子树高度1，左右子树高度差等于1，不需要进行旋转；

        第3次 4 插入5的左边，此时5的左字树高度1，右子树高度1，左右子树高度差等于0，不需要进行旋转；

        第4次 2 插入4的左边，此时4的左右子树高度差等于1，5的左右子树高度差等于1，不需要进行旋转；

        第5次 0 插入2的左边，此时4的左右子树高度差等于2，不平衡，需要进行旋转，让2成为新的根节点；

        第6次 3 插入4的左边，此时5的左右子树高度差等于2，不平衡，需要进行旋转，让4成为新的根节点；

        第7次 1 插入0的左边，此时没有不平衡，不需要进行旋转；

        第8次 6 插入7的左边，此时5的左右子树高度差等于2，不平衡，需要进行旋转，让6成为新的根节点，结束。

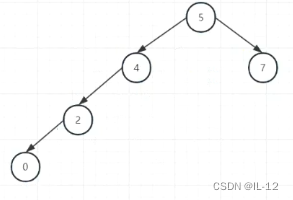（第一次旋转前）

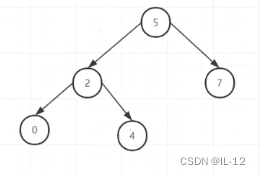（第一次旋转后）

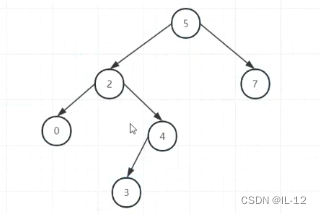（第二次旋转前）

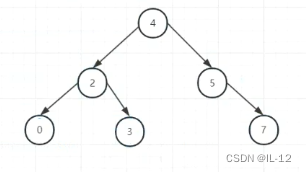（第二次旋转后）

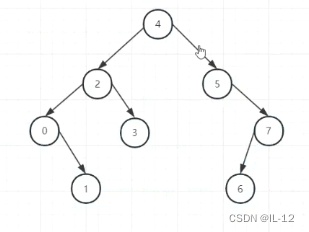（第三次旋转前）

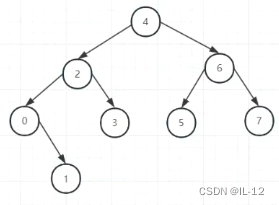（第三次旋转后 最终结果）

优缺点

优点：时间复杂度稳定在logn上；

缺点：每次旋转过分消耗计算资源。

结论

平衡二叉树同样不是我们的最优选择，于是在此基础上人们创造了红黑树（最优二叉树）。