超多目标演化算法及应用研究

最新推荐文章于 2023-01-05 17:44:25 发布

小怪兽会微笑

最新推荐文章于 2023-01-05 17:44:25 发布

阅读量2.5k

点赞数 9

分类专栏：论文陪读文章标签：算法人工智能

本文链接：https://blog.csdn.net/a1920993165/article/details/115488403

版权

论文陪读专栏收录该内容

59 篇文章

订阅专栏

超多目标演化算法及应用研究

各类优化算法入门优秀论文总结目录

1.摘要

本文是2017年中科大的计算机应用技术专业的李丙栋的博士学位论文，虽然不在顶刊上发表，但我从这篇论文上学到的远大于一般顶刊上论文。

首先，本文对超多目标演化算法进行了一个综诉（讲的非常好），还提出了一个算法，该算法是对一篇顶刊上的论文：Two-Archive Evolutionary Algorithm for Constrained Multiobjective Optimization的改进版本。
另外，本文提出了一个平衡不同性能指标影响的技术。
最后，本文还提出了一个多指标优化算法来处理超多目标优化问题。

2.介绍

概述

本文指出，自2013年以来，针对超多目标问题的文献突然变多了，其中还有发表在人工智能领域上的两篇论文，而不是专注于演化计算的期刊或会议。
下图为作者调研表：
在这里插入图片描述
基于算法的核心思想.我们将超多目标演化方法分为以下几类:基于松弛的支配定义的方法、基于多样性的方法、基于聚集的方法、基于评价指标的方法、基于参照点集的方法、基于偏好的方法和降维的方法。分类图如下：
在这里插入图片描述
每类概述如下：

基于松弛函数的方法试图通过放松传统的支配定义来提升算法的选择压力
基于多样性的方法试图通过降低多样性维持机制的副作用来提升算法的性能
基于性能指标的方法通过评价指标的数值来引导搜索过程，因为更好的指标数值通常意味着解集合是帕累托前沿的更好的逼近
基于参照点集合的方法使用了组参照点来评估非支配解的质量
基于偏好的方法通过引入用户的偏好信息来引导算法的搜索方向
基于降维的方法试图减少超多目标演化算法的口标数量，从而将原问题转化为另一个难度更低、目标数更少、但是帕累托前沿类似的问题。

多目标中的困难

当目标数量增加时，算法设计者不得不处理下面几个困难:

支配阻抗现象（Dominance resistance (DR)phenomenon):由于解集合中非支配解的占比急剧增加，导致的解之间不可比较的情况。
有限的解集合大小:在:非退化的情况下、一个m目标问题的帕累托前沿是一个(m-1)-维流形。然而．描述这一流形需要的解的个数随着标数m指数型增长。
解集合在目标空间的可视化需要设计专门的技术，如映射到低维度空间，平行坐标表示法等

本文框架
在这里插入图片描述

3.超多目标算法综述

3.1 基于松弛支配的方法

为了将超多目标优化问题中的非支配解区分开来、提升朝向帕累托前沿的选择压力，学者们提出了很多帕累托支配关系的变种。作者将这类技术分为两类:基于数值的支配和基于数量的支配。

3.1.1基于数值的支配

顾名思义，这类方法通过改变解的目标函数值来改进帕累托支配关系。总的来说.这些改动的目的在于增大非支配解的支配区域、以期提升解之间的存在支配关系的可能性。
下图是该类方法的总结：
在这里插入图片描述

3.1.2基于数量的支配

基于数值的方法试图通过比较互相优劣的目标计数来比较两个解

在这里插入图片描述

3.2基于多样性的方法

尽管现阶段的额很多研究工作集中在改进帕累托支配定义.上，但是仍有部分工作研究通过使用专用的多样性评估方法来改进超多目标演化算法。总的来说，这类方法试图通过多样性提升的副作用来改进算法性能。汇总表如下：

在这里插入图片描述

3.3基于聚集函数的方法

使用聚集函数是区分超多目标问题解的另一途径。根据聚集的信息、这类方法可以被分为两类:聚集个体信息的方法和聚集成对比较结果的方法。

3.3.1聚集个体信息的方法

这种方法通常使用聚集个体的信息来比较解。它们又可以细分为两个子类:聚集自标函数值和聚集目标的排名。见下表。
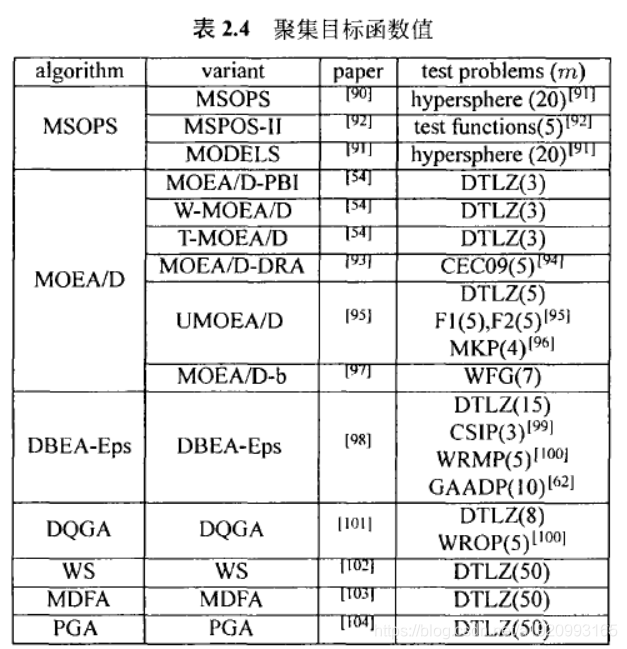
在这里插入图片描述

一、聚集目标函数值

加权和、加权切比雪夫（又称为加权最小-最大方法)、向量角度距离缩放和边界交点方法是常用的聚集函数.Garza-Fabre等人在超多目标优化问题上测试了加权和方法、其中权重系数用来表示目标的重要性。通过使用一系列的权重向量、研究者可以将-一个超多目标优化问题分解成很多个单目标优化子问题。

二、聚集目标函数排名

排序支配(Ranking Dominance )将每个目标数值的排名进行聚合。一个解排序支配另一个解当且仅当它的聚集数值比另一个解更小。论文中使用了两种聚集方法:元素之和和元素最小值,实验结果显示，排序支配比帕累托支配的收敛性更好。但是，在某些情况下．因为目标的退化，它可能回舞蹈搜索的方向，类似的方法在论文中也被提及。
在这里插入图片描述

3.3.2聚集成对比较结果的方法

除了个体信息，与种群中其他个体的成对的比较结果也可以用来聚合。

在这里插入图片描述
2.3.3讨论

尽管基于聚集的方法不依赖帕累托支配将种群向帕累托前沿推进，这类方法在处理超多目标优化问题也有着自己的困难。而这些困难也正是未来潜在的科研方向。

权重向量的设置:对于聚集个体信息的方法，权重向量对于多样性有着巨大的影响。但是如何处理有限的计算资源和指数型增长的权重向量之间的冲突，仍未有一个广泛认可的答案。
聚集函数的选择:论文川的实验结果显示MOEA/D的解集合在某些测试
样例上收敛性很好但是对于整个帕累托前沿的覆盖较差。切比雪夫函数可能会对于多样性保持造成影响,因为，有些权重向量可能对应到了同一个帕累托最优解。另一方面，加权和的方法对于非凸Pareto前沿的问题处理的并不好，未来也需要进行改进

3.4基于评价指标的方法
因为最终解集合的优劣是按照评估指标来比较的、所以使用评价指标的数值来指导搜索过程也是个直觉上比较直接的方法。根据算法使用的评价指标、我们将算法分为以下三类:基于超体积的、基于距离指标的和基于R2指标的方法。

3.4.1基于超体积的方法

超体积评估指标是唯一一个已知可以和帕累托支配关系一致的方法。它的这一性质催生了一系列的基于超体积的演化算法.
在这里插入图片描述
3.4.2基于距离指标的函数
由于计算超体积的计算代价过大、有些学者提出了基于距离指标的算法。

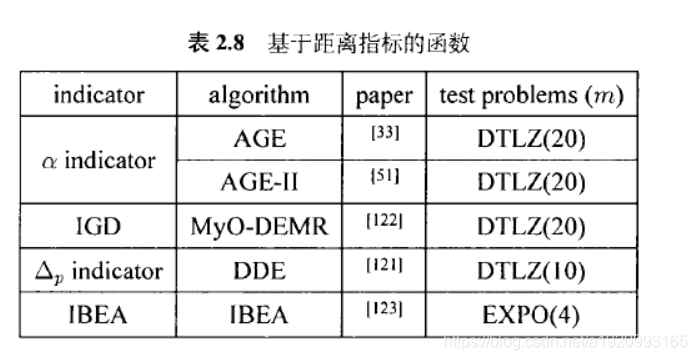
3.4.3 基于R2指标的方法
R2-MOGA and R2MODE使用了R2指标来嵌入了改进版的Goldberg 提出的非支配排序方法(non-dominated sorting method)。

在这里插入图片描述
3.4.4缺点

计算复杂度大
得到的解通常不均匀
需要参考点或参考集

3.5基于参照点集合的方法

近年来出现了一类基于参照点集的算法。这类算法依照参照点集合来评价解的优劣。因此，搜索的过程由选中的参考来指导方向。这类方法有两个关键点:(a)如何构造参照点集合（b）如何使用参考点集合比较解的优劣。
在这里插入图片描述

3.6基于偏好的方法

为了逼近超多目标优化问题的整个帕累托前沿，我们需要根据目标数目指数型地增加种群大小.但是、在处理很多现实问题时，种群大小相对于整个目标空间而言太小、以至于无法给出一个有意义的逼近.因此，根据用户的偏好﹐瞄准帕累托前沿的一个子集进行逼近看起来是个很好的想法。这类方法在文献中已有深入的讨论。
对于基于偏好的方法，两个关键点在于如何将偏好进行建模以及何时将偏好信息融入搜索过程。现存的偏好模型很多，例如目标点模型、目标折衷模型、目标排名模型等等。根据结合偏好信息和优化过程的时机，基于偏好的方法可以分为以下三类：

·先验算法(先选择后搜索):偏好信息在搜索之前定义好，并影响搜索的方向
·交互型算法(边搜索边选择):优化算法与决策者进行交互、根据决策者的反馈不断修正搜索方向、使得最终种群朝向用户感兴趣的领域
·后验型算法(先搜索后选择):偏好信息在搜索过程结束之后引入，在搜索产出的种群中再选择一个子集作为整体的输出

在这里插入图片描述

在这里插入图片描述
3.7基于降维的方法

尽管很多算法试图直接处理超多目标优化问题的困难、系列降维的方法则从另一角度入手处理问题:绕过超多目标优化问题的困难。降维方法致力于处理目标有冗余的超多日标优化问题。Ishibuchi等人指出、如果新增加的目标之间高度相关或者依赖,算法 NSGA-Il的性能并不会大幅退化。当一个高维的超多目标优化问题和另一个目标数较少的问题有相似的帕累托前沿时，我们可以尝试优化目标数较少的问题。根据降维技术的使用时机，这类算法可以分为以下两类:离线型方法和在线型方法。
在这里插入图片描述

在这里插入图片描述
3.8超多目标问题

4.改进版的两档案算法

在本章中，作者针对两档案算法的主要缺陷,提出了改进版的两档案算法(Improved Two Archive Algorithm,ITAA)在提出的算法中，作者采用基于惩罚的边界交叉方法(Penalty-based Boundary Intersection,PBI)作为CA 的截断选择策略(54})、并采用基于平移的密度估计(Shift-based Density Estimation, SDE)/551作为DA的排序策略。通过引入PBI方法、超过一定大小时CA可以进行截断。SDE则用来提升DA 的收敛性、避免其严重滞后于整个种群的收敛。实验结果显示、改进版的算法在收敛性和多样性上的总体性能都优于原版算法。

5.基于随机排序的多指标超多目标演化算法

一种处理超多目标优化问题的很直观的方法是利用解集合的性能指标来引导搜索方向。但是，单个指标函数的偏向性很有可能使得搜索算法关注帕累托前沿的某个子区域。例如基于 $I_{\epsilon+}$ 指标的算法IBEA在处理超多目标优化问题时的多样性较差。这种现象说明 $I_{\epsilon+}$ 指标相对多样性而言更加偏好收敛性更好的解。其他指标（如拥塞距离、平移密度估计 $I_{SDE}$ 等等）则偏好多样性更好的解。
由于不同的指标可能有不同的偏向性，而不同的偏向性可能相互补充，因此，使用多个指标的组合而非单个指标进行环境选择可能会得到一个更好的基于指标的算法。在这一想法的基础.上，本章针对超多目标优化问题提出了一个多指标算法。设计这样一个算法的关键问题在于如何在环境选择是组合使用很有可能互相冲突的多个性能指标。由于随机排序已经被验证在平衡约束优化中适应度和l约束违反量之间的冲突方面表现出色，所以作者采用了随机排序技术来处理多个指标的平衡问题。在一系列的测试问题上的实验结果表明，基于随机排序的多指标算法stochastic ranking based multi-indicator algorithm (SRA)都显示出很好的总体性能。
本章的主要贡献在于以下几点:

作者介绍了一种新的技术用来平衡超多同标演化算法中不同评估指标的影响。通过一个基于随机冒泡排序的排序过程,不同指标的影响得到平衡。通过一个可调节的参数，排序过程使得算法设计者可以在不同的评估指标之间做一个折衷。
为了处理需要算法具有很强收敛性的问题，一个基于方向的档案被结合到随机排序算法的框架里面，以保存收敛较好的解并帮助维持算法的多样性。
在 DTLZ和WFG两个基准测试问题集上的全面的实验结果表明、不同的测试问题集合对于各个算法有着不同的偏好。困此，在评估超多目标演化算法时，把多个数据集都包含进来很有必要。

随机排序算法

算法框架
在这里插入图片描述