蓝桥杯 格子刷油漆

<<  返回

  历届试题 格子刷油漆  

时间限制：1.0s   内存限制：256.0MB

       

问题描述

　　X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形（如下图所示），现需要把这些格子刷上保护漆。


　　你可以从任意一个格子刷起，刷完一格，可以移动到和它相邻的格子（对角相邻也算数），但不能移动到较远的格子（因为油漆未干不能踩！）
　　比如：a d b c e f 就是合格的刷漆顺序。
　　c e f d a b 是另一种合适的方案。
　　当已知 N 时，求总的方案数。当N较大时，结果会迅速增大，请把结果对 1000000007 (十亿零七) 取模。

输入格式

　　输入数据为一个正整数（不大于1000）

输出格式

　　输出数据为一个正整数。

样例输入

2

样例输出

24

样例输入

3

样例输出

96

样例输入

22

样例输出

359635897

      额额，写出来还是得靠这位大神博客的启发：http://blog.csdn.net/u010126535/article/details/20651999；

写的太好了，启发了我的思路（之前思路非常不好），我的思路基本上就是照抄他的，但是最后求解过程以及初始状态有些许不同，再次膜拜。

这位大牛解此题的关键就在于创建了两个数组，设为q2[n]和q1[n],分别存储长度为n的矩阵从一角开始遍历完后终于任意点以及终于同一列相对位置点的数量

递推关系有：

       q1[n]=q1[n-1]*2（可以根据定义以及格子关系求得）

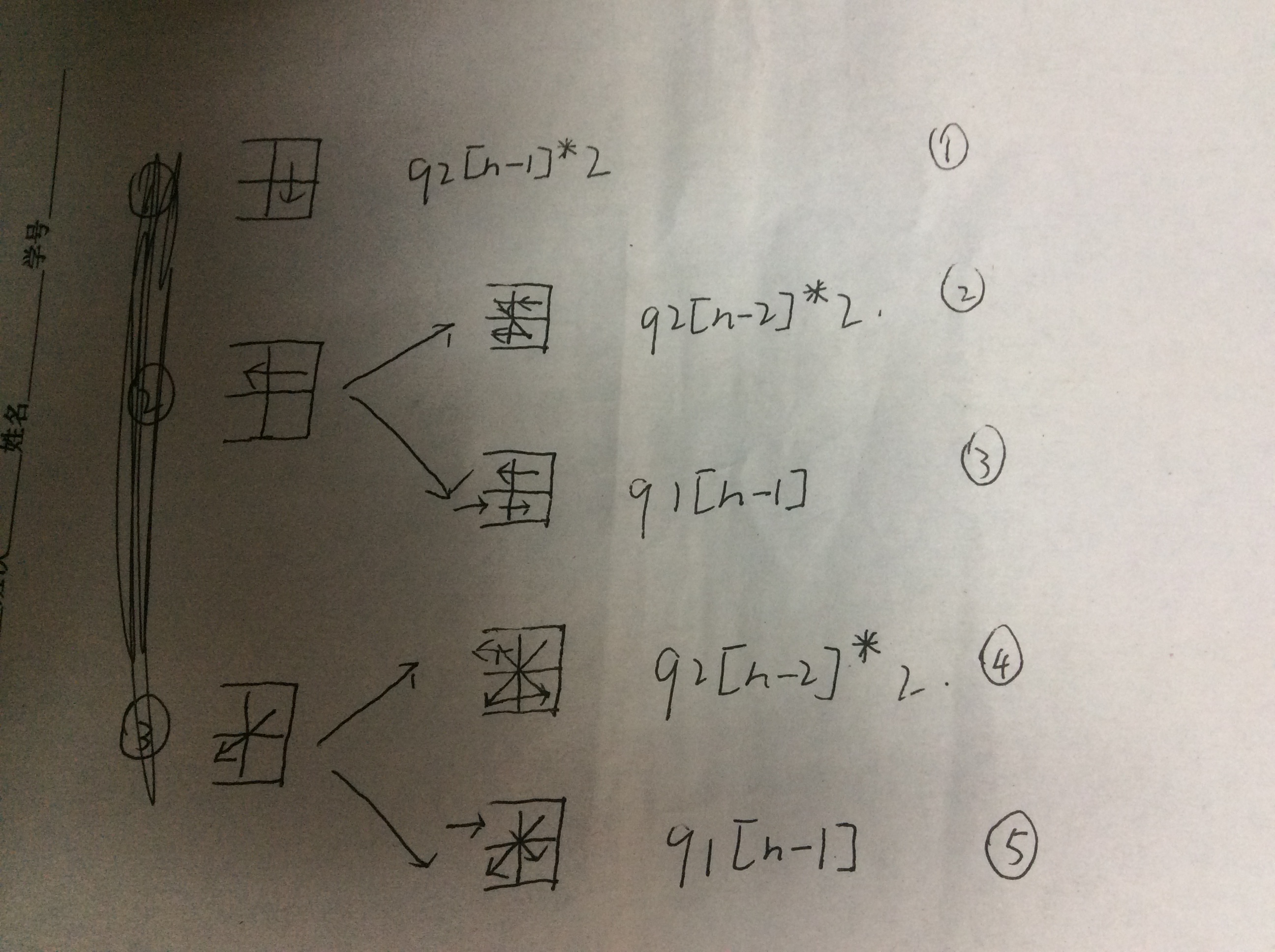
       q2[n]=q1[n-1]*2+q2[n-1]*2+q2[n-2]*4（这个式子见下图以及说明）

情况一 先去同一列相邻格子 q2[n]+=q2[n-1]*2

情况二 先去相邻列的同行格子 

         然后又有 先去右下角再来左边部分 q2[n]+=q2[n-2]*2

                          先遍历完左边部分再去左下角 q2[n]+=q1[n-1]

情况三 直接来左下角

         然后又有 先去右边格子 再遍历完左边 q2[n]+=q2[n-2]*2

                          先遍历完左边再去右边的格子 q2[n]+=q1[n-1]

整理就得出上式

最终结果就是（设矩形长度为n）

四个角作为起点的数量加上中间开始的数量

从中间某列的一点（2种选择）出发一定要先遍历完这一列的一侧并且回到这一列的另一个点（这就是q1派上用场的时候），另外一侧就直接用q2表示的数目加上好了（两种选择），所以是下式中有个4；

4*q2[n]+∑（2到n-1）（4*q1[i]*q2[n-i]+4*q1[n-i+1]*q2[i-1]）（两部分分别为先遍历左边的和先遍历右边的）

最后别忘了经常mod1000000007

下面附上奇短的代码

#include<iostream>
#define DF 1000000007
using namespace std;
long a,b,c,d,n;
long long sum,q1[1001],q2[1001];
int main()
{
	cin>>n;
	q1[1]=1;
	q2[1]=1;
	q1[2]=2;
	q2[2]=6;
	for (a=3;a<=n;a++)
	{
		q1[a]=q1[a-1]*2;
		q1[a]%=DF;
		q2[a]=q2[a-1]*2+q1[a-1]*2+q2[a-2]*4;
		q2[a]%=DF;
	}
	sum=(q2[n]*4)%DF;
	for(a=2;a<n;a++)
	sum=(sum+4*(q1[a]*q2[n-a]%DF+q1[n-a+1]*q2[a-1]%DF))%DF;
		cout<<sum<<endl;
}