part2 基于动态规划的最长公共子序列算法

最新推荐文章于 2024-07-25 11:27:31 发布

香菇包还是韭菜包

最新推荐文章于 2024-07-25 11:27:31 发布

阅读量718

点赞数 28

分类专栏：算法文章标签：算法动态规划

本文链接：https://blog.csdn.net/a1b2c3666666/article/details/138444076

版权

算法专栏收录该内容

4 篇文章 0 订阅

订阅专栏

本文详细阐述了如何使用动态规划解决最长公共子序列问题，包括问题描述、策略选择、伪代码描述、算法正确性证明、复杂性分析以及其实现与测试。重点讲解了如何构建二维数组dp，递推关系和空间优化技巧。

摘要由CSDN通过智能技术生成

1.理解问题，给出问题的描述。

2.算法设计，包括算法策略与数据结构的选择。

1.理解问题，给出问题的描述。

给定两个序列 X 和 Y，当另一个序列 Z 既是 X 的子序列又是 Y 的子序列时， Z 是 X 和 Y 的公共子序列。

2.算法设计，包括算法策略与数据结构的选择。

(1)算法策略：

①初始化一个二维数组 dp，其中 dp[i][j]表示 s1 的前 i 个字符和 s2 的前 j 个字符的最长公共子序列的长度。

②遍历两个字符串的所有字符，如果 s1[i-1] == s2[j-1]，则 dp[i][j] =dp[i-1][j-1] + 1；否则，dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

③返回 dp[m][n]，即 s1 和 s2 的最长公共子序列的长度。

(2)数据结构的选择：使用一个二维数组 dp 来存储中间结果，其中 dp[i][j]表示 s1 的前 i 个字符和 s2 的前 j 个字符的最长公共子序列的长度。

想要了解动态规划的宝宝可以康康我的这篇文章：

动态规划的基本思想https://blog.csdn.net/a1b2c3666666/article/details/138444468?spm=1001.2014.3001.5502里面详细介绍了动态规划法~

3.描述算法（伪代码）。

function LCS(s1, s2):

m = length(s1)

n = length(s2)

dp = [[0] * (n + 1) for _ in range(m + 1)]

for i in range(1, m + 1):

for j in range(1, n + 1):

if s1[i - 1] == s2[j - 1]:

dp[i][j] = dp[i - 1][j - 1] + 1

else:

dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

return dp[m][n]

4.算法的正确性证明。

(1)初始化：

当 i=0 或 j=0 时，dp[i][j]=0，因为空序列与任何序列的最长公共子序列长度为 0。

(2)递推关系：

对于任意 i>0 和 j>0，如果 s1[i-1] == s2[j-1]，那么 dp[i][j] = dp[i-1][j-1] + 1；否则，dp[i][j] = max(dp[i-1][j], dp[i][j-1])。这个递推关系保证了在每一步都能找到当前位置的最长公共子序列长度。

(3)最优解：

最后返回的 dp[m][n]就是 s1 和 s2 的最长公共子序列的长度。

5. 算法复杂性分析。

（1）时间复杂性：由于算法需要遍历两个字符串的所有字符，所以时间复杂性为 O(m*n),其中 m 和 n 分别为两个字符串的长度。

（2）空间复杂性：算法使用了一个二维数组 dp 来存储中间结果，其大小为（m+1）(n+1),所以空间复杂性为 O(mn)。

6.算法的实现与测试。

代码及运行结果截图：

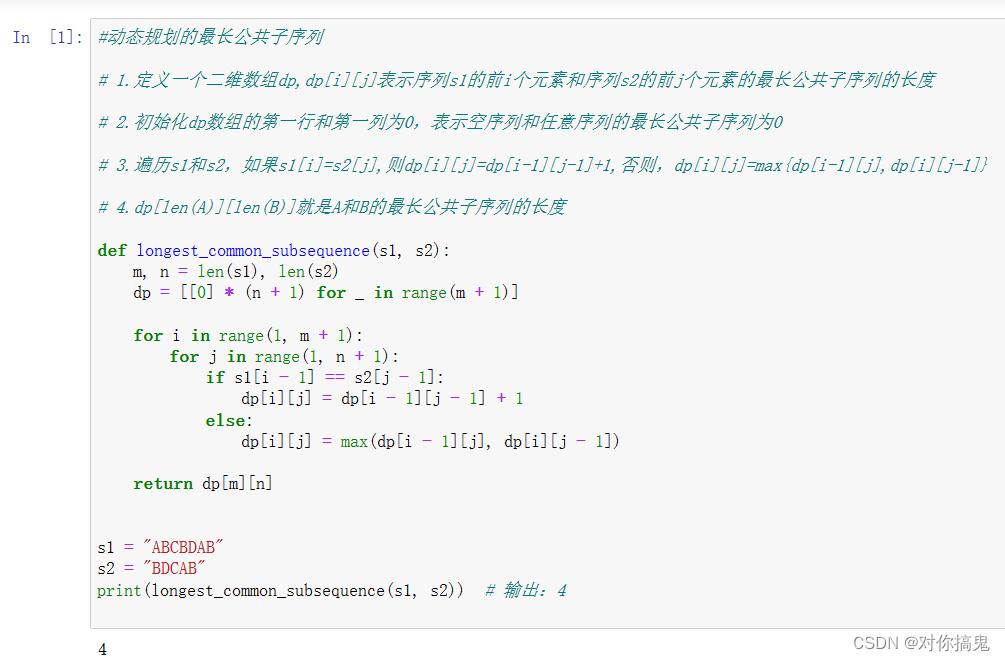
def longest_common_subsequence(s1, s2):
    m, n = len(s1), len(s2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]

    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if s1[i - 1] == s2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

    return dp[m][n]


s1 = "ABCBDAB"
s2 = "BDCAB"
print(longest_common_subsequence(s1, s2))  # 输出：4