动态规划的基本思想

目录

1.前言

2.基本思想

3.区分：动态规划法和分治法

4.适用于什么类型的问题

5.用动态规划法求解问题时的详细步骤

6.伪代码

7.总结

---

1.前言

动态规划的基本思想类似于分治法，但是由于通常情况下许多子问题可能是相同的，所以动态规划法仅对每个子问题求解一次，这样就减少了计算量。 也就是说 —— 一旦某个给定子问题的解已经算出，则以填表形式将它存储，下次需要时直接拿出来用就好了。

想要了解分治法基本思想的宝宝可以康康我的这篇文章：

分治法的基本思想及步骤https://blog.csdn.net/a1b2c3666666/article/details/138425914?spm=1001.2014.3001.5502

简单说明了动态规划是怎么一回事儿，接下来我们来系统详细地梳理一遍ovo

2.基本思想

（1）分治：

        将原问题分解为更小、更易求解的子问题，然后对子问题进行求解，并最终产生原问题的解

（2）解决冗余：

        求解过程中，所有子问题只求解一次并以表的方式保存，对于相同子问题并不重复求解而通过查表的方式获得。

3.区分：动态规划法和分治法

（1）相同之处：基于分治思想

（2）不同之处：分治法中各个子问题是独立的，而动态规划方法中允许子问题之间存在重叠。

4.适用于什么类型的问题

什么类型的问题适合用动态规划法来解决呢？

（1）最优子结构：

        问题可以分解为子问题，且这些子问题的最优解可以组合成原问题的最优解。

（2）重叠子问题：

        在解决过程中，相同的子问题会被多次遇到，可以通过存储这些子问题的解来提高效率。

（3）无后效性：

        某阶段状态一旦确定，就不会受到之后阶段决策的影响

5.用动态规划法求解问题时的详细步骤

（1）定义状态：

        确定问题的状态，即描述问题的变量和参数。

（2）初始化边界条件：

        确定问题的初始状态或边界情况，作为递推的基础。

（3）确定状态转移方程：

        根据问题的特点，确定状态之间的关系，即如何从前一个或多个状态转移到下一个状态。

（4）迭代计算：

        从基础情况出发，逐步构建出整个问题的解。

（5）返回结果：

        根据最终的状态，得到问题的最优解。

6.伪代码

在这里我们以斐波那契数列（兔子数列）为例,来计算第n项的值：

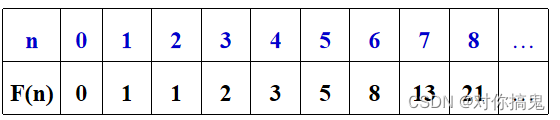
伪代码如下：

def fibonacci(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    dp = [0] * (n+1)                   //用列表dp来存储已经计算过的斐波那契数列的值，避免重复计算
    dp[0] = 0
    dp[1] = 1
    for i in range(2, n+1):
        dp[i] = dp[i-1] + dp[i-2]   //通过递推关系，逐步计算出第n项的值
    return dp[n]                       //返回dp[n]即为所求的斐波那契数列的第n项

7.总结

        动态规划在计算机科学、运筹学、经济学等领域都有广泛的应用，特别是在算法竞赛和面试中，动态规划问题经常出现，掌握动态规划对于解决这类问题至关重要。