AOJ 1313 Intersection of Two Prisms （数值积分）

Intersection of Two Prisms

Suppose that P1 is an infinite-height prism whose axis is parallel to the z-axis, and P2 is also an infinite-height prism whose axis is parallel to the y-axis. P1 is defined by the polygon C1 which is the cross section of P1 and the xy-plane, and P2 is also defined by the polygon C2 which is the cross section of P2 and thexz-plane.

Figure I.1 shows two cross sections which appear as the first dataset in the sample input, and Figure I.2 shows the relationship between the prisms and their cross sections.

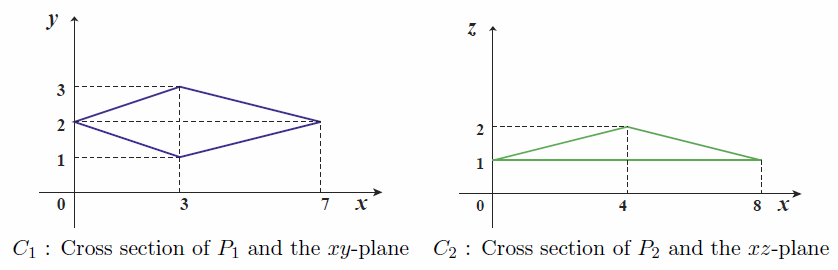
Figure I.1: Cross sections of Prisms

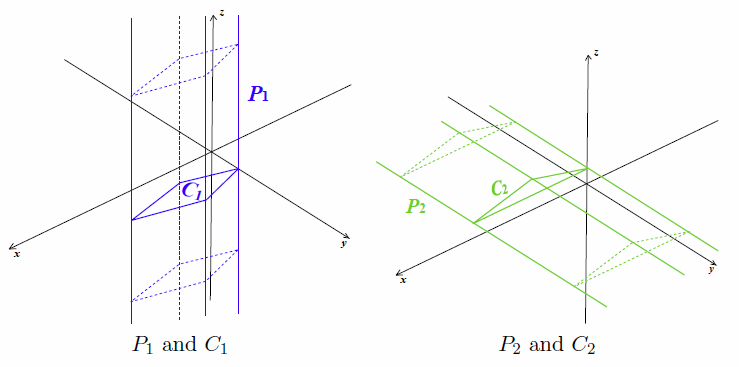
Figure I.2: Prisms and their cross sections

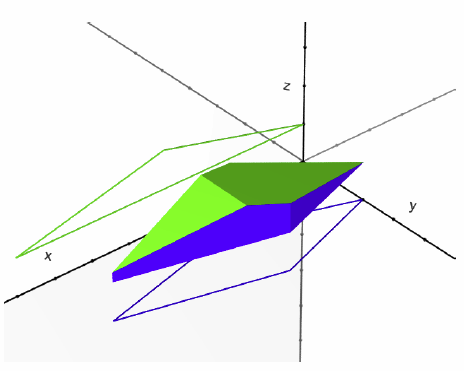
Figure I.3: Intersection of two prisms

Figure I.3 shows the intersection of two prisms in Figure I.2, namely, P1 and P2.

Write a program which calculates the volume of the intersection of two prisms.

Input

The input is a sequence of datasets. The number of datasets is less than 200.

Each dataset is formatted as follows.

m n
x11 y11
x12 y12 
.
.
.
x1m y1m 
x21 z21
x22 z22
.
.
.
x2n z2n

m and n are integers (3 ≤ m ≤ 100, 3 ≤ n ≤ 100) which represent the numbers of the vertices of the polygons, C1 and C2, respectively.

x1i, y1i, x2j and z2j are integers between -100 and 100, inclusive. (x1i, y1i) and (x2j , z2j) mean the i-th and j-th vertices' positions of C1 and C2 respectively.

The sequences of these vertex positions are given in the counterclockwise order either on the xy-plane or the xz-plane as in Figure I.1.

You may assume that all the polygons are convex, that is, all the interior angles of the polygons are less than 180 degrees. You may also assume that all the polygons are simple, that is, each polygon's boundary does not cross nor touch itself.

The end of the input is indicated by a line containing two zeros.

Output

For each dataset, output the volume of the intersection of the two prisms, P1 and P2, with a decimal representation in a line.

None of the output values may have an error greater than 0.001. The output should not contain any other extra characters.

Sample Input

4 3
7 2
3 3
0 2
3 1
4 2
0 1
8 1
4 4
30 2
30 12
2 12
2 2
15 2
30 8
13 14
2 8
8 5
13 5
21 7
21 9
18 15
11 15
6 10
6 8
8 5
10 12
5 9
15 6
20 10
18 12
3 3
5 5
10 3
10 10
20 8
10 15
10 8
4 4
-98 99
-99 -99
99 -98
99 97
-99 99
-98 -98
99 -99
96 99
0 0

Output for the Sample Input

4.708333333333333
1680.0000000000005
491.1500000000007
0.0
7600258.4847715655

---

题意：

有一个侧棱与z轴平行的棱柱P1和一个侧棱与y轴平行的棱柱P2。他们都向两端无限延伸，地面分别是包含M个顶点和N个顶点的凸多边形，其中第i个顶点的坐标分别是(X1i,Y1i)和(X2i, Z2i)。请计算这两个棱柱公共部分的体积。

分析：

首先会想到先求出公共部分的凸多面体的顶点坐标，然后在计算其体积的这一方法，公共部分的凸多面体的顶点都是一个棱柱的侧面与另一个棱柱的侧棱的交点，可以通过O(nm)时间的枚举求得，因而这一方法貌似很合理。但因为涉及三维空间的几何运算，实现起来非常麻烦。

事实上，只要沿着x轴对棱柱切片，就可以非常简洁的解决这道问题。我们按某个x值对侧棱与z轴平行的棱柱P1切片后，就得到了[y1,y2] * (-oo, oo)这样的在z轴方向无限延伸的长方形的横截面。同样的，我们按某个x值对侧棱与y轴平行的棱柱P2切片后，就得到了(-oo,oo) * [z1, z2]这样的在y轴方向无限延伸的长方形的横截面。因此，我们按某个x值对两个棱柱的公共部分切片后，得到的横截面就是长方形[y1, y2] *[z1, z2]。而长方形的面积通过(y2 –y1) * (z2 – z1)就可以轻松求得，之后只要关于x轴对面积求积分就能得到公共部分的体积了。

首先，我们枚举出原棱柱底面顶点的所有x坐标并排序。于是，在相邻两个x坐标之间的区间中，按x值切片得到的长方形的顶点坐标是关于x的线性函数，所以面积就是关于x的二次函数，其积分很容易计算。虽然可以通过求得表达式后再计算二次函数的积分，不过利用下面的Simpson公式则更为轻松。

 

Simpson公式就是在数值积分中用二次函数来近似原函数进行积分而得到的公式。如果原函数本身就是次数不超过二的多项式的话，那么通过该公式就可以求得精确的积分值。利用该公式，我们就无需求出关于x的多项式，而只要计算按区间的端点和中点切片得到长方形的面积就足够了。

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 100 + 10;
const int INF = 100000000;

int M, N;
int X1[maxn], Y1[maxn];
int X2[maxn], Z2[maxn];

//计算按x值对多边形切片得到的宽度
double width(int* X, int* Y, int n, double x)
{
    double lb = INF, ub = -INF;
    for (int i = 0; i < n; i++){
        double x1 = X[i], y1 = Y[i], x2 = X[(i + 1) % n], y2 = Y[(i + 1) % n];
        //检查与第i条边是否相交
        if ((x1 - x) * (x2 - x) <= 0 && x1 != x2){
            //计算交点的坐标
            double y = y1 + (y2 - y1) * (x - x1) / (x2 - x1);
            lb = min(lb, y);
            ub = max(ub, y);
        }
    }
    return max(0.0, ub - lb);
}

void solve()
{
    //枚举区间的端点
    int min1 = *min_element(X1, X1 + M);
    int max1 = *max_element(X1, X1 + M);
    int min2 = *min_element(X2, X2 + N);
    int max2 = *max_element(X2, X2 + N);
    vector<int> xs;
    for (int i = 0; i < M; i++)
        xs.push_back(X1[i]);
    for (int i = 0; i < N; i++)
        xs.push_back(X2[i]);
    sort(xs.begin(), xs.end());

    double res = 0;
    for (int i = 0; i + 1 < xs.size(); i++){
        double a = xs[i], b = xs[i + 1], c = (a + b) / 2;
        if (min1 <= c && c <= max1 && min2 <= c && c <= max2){
            //利用Simpson公式求积分
            double fa = width(X1, Y1, M, a) * width(X2, Z2, N, a);
            double fb = width(X1, Y1, M, b) * width(X2, Z2, N, b);
            double fc = width(X1, Y1, M, c) * width(X2, Z2, N, c);
            res += (b - a) / 6 * (fa + 4 * fc + fb);
        }
    }
    printf("%.10f\n", res);
}

int main()
{
    while (scanf("%d%d", &M, &N), M || N){
        for (int i = 0; i < M; i++){
            scanf("%d%d", &X1[i], &Y1[i]);
        }
        for (int i = 0; i < N; i++){
            scanf("%d%d", &X2[i], &Z2[i]);
        }
        solve();
    }
    return 0;
}