-
3 3 50 3 1 1 4 5 1 5 6 7 4 100 1 2 3 4 5 6 7 1 1 7
样例输出
-
3 0
1
-
思路:求算出每个数字对于的LED数码管的编号,再算出每一个编号的数码管对应的可以显示的数字。用二维数组保存,作为标记。
-
再求出每一行LED编号,都满足的数字有哪些,与对于的n的每一位相比较,比n小的才满足。
-
看每一位有多少个数字满足,然后相乘即为结果。
-
因为我是比赛结束才做的,晚上题目还没有挂出来,还没提交,暂时还不知道是否能AC,写的挺匆忙,代码也挺凌乱的,不好意思。
-
#include <iostream> #include <cstdio> #include <string.h> #include <algorithm> using namespace std; int fla[8][10]={{}, {1,0,1,0,0,1,1,1,1,1}, {1,0,0,0,1,1,1,0,1,1}, {1,0,1,1,1,0,0,1,1,1}, {0,0,1,1,1,1,1,0,1,1}, {1,0,1,0,0,0,1,0,1,0}, {1,1,0,1,1,1,1,1,1,1}, {1,0,1,1,0,1,1,0,1,1}}; /*第n个管亮,对应的可以表示的数字 1:0,2,5,6,7,8,9 2:0,4,5,6,8,9 3:0,2,3,4,7,8,9 4:2,3,4,5,6,8,9 5:0,2,6,8 6:0,1,3,4,5,6,7,8,9 7:0,2,3,5,6,8,9 */ int main() { int S; cin>>S; while(S--){ int k; char n[11]; scanf("%d %s%*c",&k,n); int len=strlen(n); if(k>len){//当k大于n的位数的时候,字符串右移,左边补0,方便后来的比较 for(int i=len;i>=0;i--) n[i+k-len]=n[i]; for(int i=0;i<k-len;i++) n[i]='0'; } int ans[6]={0},out=1; int fla2=0; for(int i=0;i<k;i++){ char t[999]; gets(t); int num[11]={0}; int fla1[6]={0}; for(int j=0;j<strlen(t);j++){ if(t[j]>='1'&&t[j]<='7'){ fla1[i]++; for(int k=0;k<10;k++){ if(fla[t[j]-'0'][k]){ num[k]++; } } } } for(int j=0;j<10;j++){ if(fla2==0){ if(num[j]==fla1[i]&&j<=n[i]-'0'){ //当满足要求的数字个数,等于每行输入的LED灯的个数,且数字小于n的第i位时,才可以 ans[i]++; } } else{ if(num[j]==fla1[i]) ans[i]++; } } if(n[i]>'0')fla2=1;//当n的某一位大于0时,后面的数字就不需要比n[i]小了 out *=ans[i]; } printf("%d\n",out); } return 0; }感谢 qq_32400847的提醒,上面代码的确是有二个错误。
-
1.我的数组第一行中把LED灯1对应数字3写掉了。
-
2.后面求出符合要求的数字后,进行排列组合的思路有问题,
-
当符合要求的数字有等于n的第i位时,就会多计算进去。
-
-
改进后的代码如下:
-
#include <iostream> #include <cstdio> #include <string.h> #include<vector> #include<algorithm> #include<map> #include<set> using namespace std; int fla[8][10]={{}, {1,0,1,1,0,1,1,1,1,1}, {1,0,0,0,1,1,1,0,1,1}, {1,0,1,1,1,0,0,1,1,1}, {0,0,1,1,1,1,1,0,1,1}, {1,0,1,0,0,0,1,0,1,0}, {1,1,0,1,1,1,1,1,1,1}, {1,0,1,1,0,1,1,0,1,1}}; /*第n个管亮,对应的可以表示的数字 1:0,2,3,5,6,7,8,9 2:0,4,5,6,8,9 3:0,2,3,4,7,8,9 4:2,3,4,5,6,8,9 5:0,2,6,8 6:0,1,3,4,5,6,7,8,9 7:0,2,3,5,6,8,9 */ int main() { int S; cin>>S; while(S--){ int k; char n[11]; scanf("%d %s%*c",&k,n); int len=strlen(n); if(k>len){//当k大于n的位数的时候,字符串右移,左边补0,方便后来的比较 for(int i=len;i>=0;i--) n[i+k-len]=n[i]; for(int i=0;i<k-len;i++) n[i]='0'; } vector< vector<int> > v(k); int fla1[6]={0}; for(int i=0;i<k;i++){ char t[999]; gets(t); int num[11]={0}; for(int j=0;j<strlen(t);j++){ if(t[j]>='1'&&t[j]<='7'){ fla1[i]++; for(int k=0;k<10;k++){ if(fla[t[j]-'0'][k]){ num[k]++;//求出满足每一行输入的LED的 数字个数 } } } } for(int j=9;j>=0;j--){ if(num[j]==fla1[i]){//当数字个数等于每一行输入的LED的数量时,该数字符合要求 v[i].push_back(j);//把满足要求的数存入V里 } } } int ans=0; for(int i=0;i<k;i++){ for(int j=0;j<v[i].size();j++){ if(v[i][j]<n[i]-'0'){ int t=1; for(int l=i+1;l<k;l++){ t*=v[l].size(); } ans+=t; } } } printf("%d\n",ans); } return 0; }
-
描述
电子数字在生活中很常见,而许多的电子数字是由LED数码管制作而成。数字LED数码管一般由7个发光二极管封装在一起,组成'8'字型,引线在内部连接完成。如下图所示,我们可以对每个发光管进行编码从1到7。而数字0到数字9可以由这七根发光管的亮暗来表示。

对LED数码管的二极管进行编码
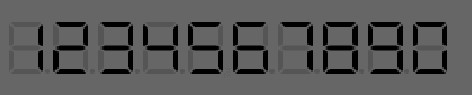
用LED数码管表示数字0-9
假设我们现在有从左到右排列好的K个LED数码管,并且我们已知每个数码管当前有哪些编号的二极管是亮着的,另外剩余的二极管由于某些原因,我们并不清楚它们的亮暗情况。由于已经有部分二极管是确定亮着的,所以每个LED数码管能表示的数字范围会有所缩小,譬如假设1号二极管已经确定是亮着的状态,那么这个LED数码管就不能表示数字1和4。
我们想知道的是,给定一个数N,在这K个LED数码管的当前亮暗的状态下,所有可能表示的数中,比N小的数有多少个。
注意,前导0是必须的,假设有4个数码管的话,'0000'表示0,'0123'表示123,即每个数的表示方法唯一。
输入
每个输入数据包含多个测试点。
第一行为测试点的个数 S ≤ 100。之后是 S 个测试点的数据。测试点之间无空行。
每个测试点的第一行为 K(1 ≤ K ≤ 5)和N(0 ≤ N ≤ 109)。之后是K行,每行表示对应数码管已点亮的二极管的情况。每行至少包含一个数字,表示对应点亮的二极管的编号,即每个数码管至少有一根二极管是点亮的。二极管编号的范围保证在1到7之间,且每行无重复编号。
注意表示数码管点亮情况的每行数字之间以及行首行末之间可能存在冗余空格,每行的字符总长度不超过100。
输出
对于每个测试点,对应的结果输出一行,表示这K个数码管在当前状态下,所有可能表示的数中,比N小的数有多少个。
样例解释
第一个样例中,只有'020', '026', '028'符合要求。
第三个样例中,只有'000'符合要求。






















 580
580

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








