（一）傅里叶变换：傅里叶级数（Fourier Series）

信号的正交分解到傅里叶级数（FS）

一、信号分解为正交函数

详见完备正交集，函数/信号的正交分解

二、傅里叶级数的三角形式

由（一）可知，可将一个周期为T的信号f(T)，在（t0,t0+T）内表示为三角函数集的线性组合，即：

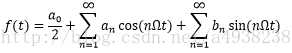
上式即为周期信号f(t)，在区间（t0,t0+T）内的三角傅里叶级数展开式。Ω=2π/T称为基波角频率。

需要指出，并非任意周期信号都能进行傅里叶级数展开。被展开的周期信号f(t)必须满足狄里赫利(Dirichlet)条件：

即在一个周期内：

（1）函数连续或只有有限个第一类间断点；

（2）函数极大值或极小值的数目应为有限个；

（3）函数是绝对可积的。

若f(t)满足狄里赫利条件，可得其各系数为：

计算得：

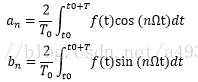
若对傅里叶级数进行-到的积分，可得

解得：

这里把a0/2写成了A0，道理是一样的

 

周期信号f(t)与其对应的频谱：

 

 

三、傅里叶级数的指数形式（简称傅里叶级数）

三角形式的傅里叶级数含义比较明确，但运算常感不便。对于一个周期为T的信号f(t)还可以表示为指数型的傅里叶级数。

因为负指数函数集在(t0,t0+T)内为完备正交函数集，所以f(t)可被负指数函数集中各个函数的线性组合表示，其傅里叶系数Fn为：

所以f(t)可以表示为：