（二）傅里叶变换：傅里叶变换、傅里叶变换的推导（Continuous Time Fourier Transform）

Norstc

于 2017-11-05 10:49:50 发布

阅读量8.9k

点赞数 1

分类专栏：信号与系统文章标签：通信数学

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/a493823882/article/details/78447931

版权

信号与系统专栏收录该内容

28 篇文章

订阅专栏

一、从傅里叶级数到（连续时间）傅里叶变换（CTFT）FS->CTFS

设某一周期信号的傅里叶系数为Fn，将f(t)展开成指数形式可得：

$f(t)=\sum_{n=-\infty}^{\infty} F_ne^{jn\Omega t}$

其傅里叶系数为：

$F_n=\frac1T\int_{t_0}^{t_0+T}f(t)e^{-jn\Omega t}\rm dt$

其中， $\Omega=\frac{2\pi}{T}$

两边同时乘以T，即同时除以1/T，得：

对于非周期信号，T->∞时，有：

$\Omega\rightarrow \rm d \omega, n\Omega\rightarrow \omega$ ①

$\frac1T=\frac{\Omega}{2\pi}\rightarrow \frac{\rm d \omega}{2\pi}$ ②

谱线间隔Ω趋近于无穷小dw，离散频率nΩ变成连续频率w，信号的频谱变成连续频谱。

在这种情况下，FnT=2πFn/Ω可能趋于一有限值，记作F(jw)，称为频谱密度函数，简称频谱函数。

首先是傅里叶系数，根据①式：

$\lim_{T\rightarrow \infty}F_n(\Omega)T=F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}\rm dt$

( F_n*T=F_n/(1/T)=F_n/f ，频谱密度即单位频率上的频谱）

然后是傅里叶级数，根据②式：

$f(t)=\frac1{2\pi}\sum_{n=-\infty}^{\infty} F_nTe^{jn\Omega t}\frac{2\pi}{T}$

当T趋于无限大，FnT变为Fjw，求和变积分，谱线间隔变微分，傅里叶级数变为：

$f(t)=\frac1{2\pi}\int_{-\infty}^{\infty} F(j\omega)e^{j\omega t}\rm d\omega$

二、傅里叶变换

将F(jw)与f(t)重新列写为一对傅里叶变换式

$F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}\rm dt$

$f(t)=\frac1{2\pi}\int_{-\infty}^{\infty} F(j\omega)e^{j\omega t}\rm d\omega$

F(jw)称为f(t)的傅里叶变换，或频谱密度函数，简称频谱。

f(t)称为F(jw)的傅里叶反变换或原函数。

频谱一般是复函数，还可写作：

|F(jw)|称为幅度谱，φ(w)称为相位谱。

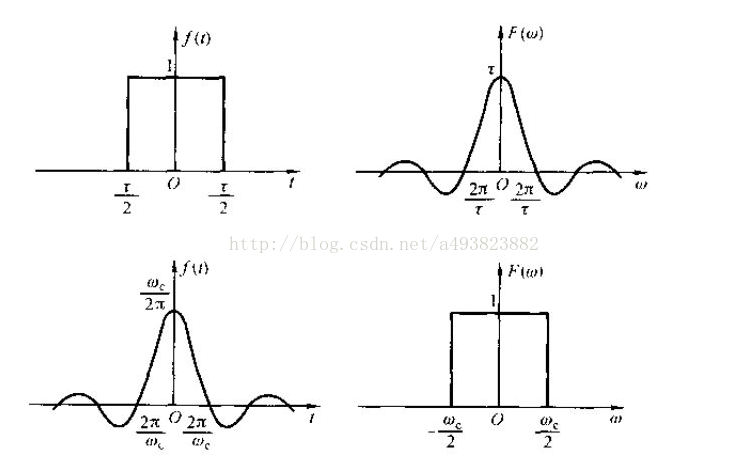
时域连续函数与其频谱图示：

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。