NBUT 1640多边形的公共部分+多边形面积交

Description

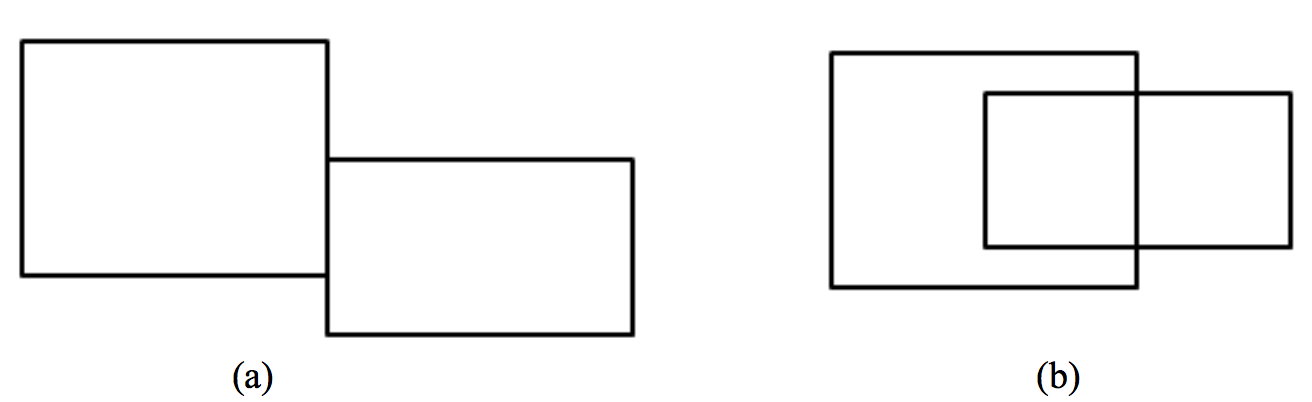
给定两个简单多边形,你的任务是判断二者是否有面积非空的公共部分。如下图,(a)中的两个矩形只有一条公共线段,没有公共面积。

在本题中,简单多边形是指不自交(也不会接触自身)、不含重复顶点并且相邻边不共线的多 
边形。

注意:本题并不复杂,但有很多看上去正确的算法实际上暗藏缺陷,请仔细考虑各种情况。

Input 
输入包含不超过 100 组数据。每组数据包含两行,每个多边形占一行。多边形的格式是:第一 个整数 n 表示顶点的个数 (3<=n<=100),接下来是 n 对整数(x,y) (-1000<=x,y<=1000),即多边 形的各个顶点,按照逆时针顺序排列。

Output 
对于每组数据,如果有非空的公共部分,输出”Yes”,否则输出”No”。

Sample Input

4 0 0 2 0 2 2 0 2 
4 2 0 4 0 4 2 2 2 
4 0 0 2 0 2 2 0 2 
4 1 0 3 0 3 2 1 2

Sample Output

Case 1: No 
Case 2: Yes

Hint

无

直接求连个多边形的面积交。。这里有可能是凹边形。所以用三角划分的办法求。（直接半平面交的话。。一直wa）.最最坑的一点。求出的面积>0wa了。而面积>eps过了。。。（卧槽啊）。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<map>
#include<stack>
#include<set>

using namespace std;

const int maxn=555;
const int maxisn=10;
const double eps=1e-8;
const double pi=acos(-1.0);

int dcmp(double x)
{
    if(x>eps) return 1;
    return x<-eps ? -1 : 0;
}
inline double Sqr(double x)
{
    return x*x;
}
struct Point
{
    double x,y;
    Point()
    {
        x=y=0;
    }
    Point(double x,double y):x(x),y(y) {};
    friend Point operator + (const Point &a,const Point &b)
    {
        return Point(a.x+b.x,a.y+b.y);
    }
    friend Point operator - (const Point &a,const Point &b)
    {
        return Point(a.x-b.x,a.y-b.y);
    }
    friend bool operator == (const Point &a,const Point &b)
    {
        return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
    }
    friend Point operator * (const Point &a,const double &b)
    {
        return Point(a.x*b,a.y*b);
    }
    friend Point operator * (const double &a,const Point &b)
    {
        return Point(a*b.x,a*b.y);
    }
    friend Point operator / (const Point &a,const double &b)
    {
        return Point(a.x/b,a.y/b);
    }
    friend bool operator < (const Point &a, const Point &b)
    {
        return a.x < b.x || (a.x == b.x && a.y < b.y);
    }
    inline double dot(const Point &b)const
    {
        return x*b.x+y*b.y;
    }
    inline double cross(const Point &b,const Point &c)const
    {
        return (b.x-x)*(c.y-y)-(c.x-x)*(b.y-y);
    }

};

Point LineCross(const Point &a,const Point &b,const Point &c,const Point &d)
{
    double u=a.cross(b,c),v=b.cross(a,d);
    return Point((c.x*v+d.x*u)/(u+v),(c.y*v+d.y*u)/(u+v));
}
double PolygonArea(Point p[],int n)
{
    if(n<3) return 0.0;
    double s=p[0].y*(p[n-1].x-p[1].x);
    p[n]=p[0];
    for(int i=1; i<n; i++)
    {
        s+=p[i].y*(p[i-1].x-p[i+1].x);
    }
    return fabs(s*0.5);
}
double CPIA(Point a[],Point b[],int na,int nb)
{
    Point p[maxisn],temp[maxisn];
    int i,j,tn,sflag,eflag;
    a[na]=a[0],b[nb]=b[0];
    memcpy(p,b,sizeof(Point)*(nb+1));
    for(i=0; i<na&&nb>2; ++i)
    {
        sflag=dcmp(a[i].cross(a[i+1],p[0]));
        for(j=tn=0; j<nb; ++j,sflag=eflag)
        {
            if(sflag>=0) temp[tn++]=p[j];
            eflag=dcmp(a[i].cross(a[i+1],p[j+1]));
            if((sflag^eflag)==-2)
                temp[tn++]=LineCross(a[i],a[i+1],p[j],p[j+1]);
        }
        memcpy(p,temp,sizeof(Point)*tn);
        nb=tn,p[nb]=p[0];
    }
    if(nb<3) return 0.0;
    return PolygonArea(p,nb);
}
double SPIA(Point a[],Point b[],int na,int nb)
{
    int i,j;
    Point t1[4],t2[4];
    double res=0.0,if_clock_t1,if_clock_t2;
    a[na]=t1[0]=a[0];
    b[nb]=t2[0]=b[0];
    for(i=2; i<na; i++)
    {
        t1[1]=a[i-1],t1[2]=a[i];
        if_clock_t1=dcmp(t1[0].cross(t1[1],t1[2]));
        if(if_clock_t1<0) swap(t1[1],t1[2]);
        for(j=2; j<nb; j++)
        {
            t2[1]=b[j-1],t2[2]=b[j];
            if_clock_t2=dcmp(t2[0].cross(t2[1],t2[2]));
            if(if_clock_t2<0) swap(t2[1],t2[2]);
            res+=CPIA(t1,t2,3,3)*if_clock_t1*if_clock_t2;
        }
    }
    return res;
    //return PolygonArea(a,na)+PolygonArea(b,nb)-res;
}

Point a[222],b[222];
Point aa[222],bb[222];

int main()
{
    int n1,n2;
    int cas=0;
    while(scanf("%d",&n1)!=EOF)
    {
        for(int i=0; i<n1; i++) scanf("%lf %lf",&a[i].x,&a[i].y);
        scanf("%d",&n2);
        for(int i=0; i<n2; i++) scanf("%lf %lf",&b[i].x,&b[i].y);
        if(fabs(SPIA(a,b,n1,n2))>eps) printf("Case %d: Yes\n",++cas);
        else printf("Case %d: No\n",++cas);
    }
    return 0;
}