训练第五周之Dijkstra算法

http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html（作者:华山大师兄）这是某大神文章，我觉得讲得非常清晰生动，本篇也复制了大神很多东西，所以在此注明，希望大家去支持大神。

---

Dijkstra算法：

一、定义：

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。一般做题的时候如果给出了起点终点的话就基本可以确定用Dijkstra算法了。

二、描述：

设G=(V,E)是一个带权图，求从结点v0到结点vn的最短路径。我们可以把图中结点分为两部分，一部分在集合S中，表示已经确定了从v0到vi的最短路径的结点集合，并且是按最短路径长度从小到大依次加入S中；另一部分在U中，表示还没确定最短路径的结点。每次在U中找到从v0到vj路径长度最短的那个结点加入到S中，直到所有结点都在S中结束。

三、步骤：

定义dist[i]表示从v0到vi的最短路径；road[a][b]为题目所给矩阵，有路则标权值，无路标INF，本身标0，可自行画成图更清晰；S[i]表示已经确定了从v0到vi最短路径长度的结点集合，初始S[i]=false；mindist为v0到U中集合的最短路径长度，初始为INF

1.把road[v0][i]赋给dist[i]，并把S[i]初始化false

2.把v0放入集合S中，即令S[v0]=1，dist[v0]=0

3.找到v0到集合U中路径长度最短的结点u

4.把u放入集合S中，令S[u]=1；并更新v0到U中所有点的路径，即如果dist[j]>dist[u]+road[u][j],就把后者赋给前者

5.U中是否还有结点，如果有重复4和5，如果没有则最短路径已找到

四、附图(从大神那复制过来的，因为超有感觉)：

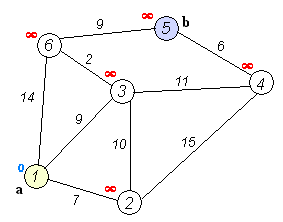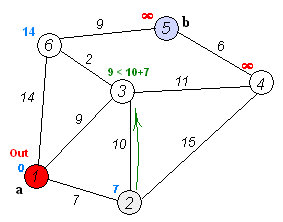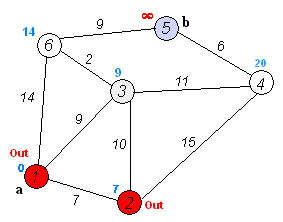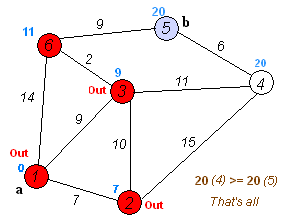
五、核心代码(当然抄了大神的)：

#define INF 99999999 /*我们通常将正无穷定义为99999999，因为这样即使两个正无穷相加，其和仍然不超过int类型的范围（C语言int类型可以存储的最大正整数是2147483647）*/
int road[MAXNUM][MAXNUM];           //题目所给矩阵，有路标权值，无路标INF，本身到本身则标0
long long dist[MAXNUM];             //从v0到vi的最短路径
bool s[MAXNUM];                     //表示已经确定了从v0到vi最短路径长度的结点集合
//int pre[MAXNUM];                 //如果题目要求输出路线，就用pre来记录前项，本来用的prev结果CE了
int n;                              //n为结点个数
void Dijkstra(int v0)               //v0为起点
{
    int i,j,u;
    for(i=1;i<=n;i++)       
    {
        dist[i]=road[v0][i];        //按题目所给矩阵初始化dist[i]的值
        s[i]=false;                 //清空集合S
        /*if(dist[i] == MAXINT)     //初始化prev[i]值，没有前项则为-1，有则为v0
            　　pre[i] = -1;
 　　     else 
            　　pre[i] = v0;*/
    }
    dist[v0]=0;
    s[v0]=true;                     //讲v0加入集合S
    for(i=2;i<=n;i++)
    {
        int mindist=INF;            //mindist为v0到U中集合的最短路径长度
        int u=v0;           
        for(j=1;j<=n;j++)           //找到v0到集合U中路径长度最短的结点u
        {
            if(!s[j]&&dist[j]<mindist)
            {
                mindist=dist[j];
                u=j;
            }
        }
        s[u]=true;                  //把u放入集合S中
        for(j=1;j<=n;j++)           //更新v0到U中所有点的路径
        {
            if(!s[j]&&road[u][j]<INF)
                if(dist[j]>road[u][j]+dist[u])
                {
                    dist[j]=road[u][j]+dist[u];
                    //pre[j] = u;  //记录前驱顶点 
                }
        }
    }
}

六、例题：

1、最短路-hdu2544

题目概述：给定n个路口，m条路，以及走每一条路的时间，帮工作人员找到从商场到到赛场花时间最短的路线，输出最短时间

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define INF 99999999
int road[105][105];
long long dist[105];
bool s[105];
int n,m;
void Dijkstra(int v0)
{
    int i,j,u;
    for(i=1;i<=n;i++)
    {
        dist[i]=road[v0][i];
        s[i]=false;
    }
    dist[v0]=0;
    s[v0]=true;
    for(i=2;i<=n;i++)
    {
        int mindist=INF;
        int u=v0;
        for(j=1;j<=n;j++)
        {
            if(!s[j]&&dist[j]<mindist)
            {
                mindist=dist[j];
                u=j;
            }
        }
        s[u]=true;
        for(j=1;j<=n;j++)
        {
            if(!s[j]&&road[u][j]<INF)
                if(dist[j]>road[u][j]+dist[u])
                {
                    dist[j]=road[u][j]+dist[u];
                }
        }
    }
    printf("%lld\n",dist[n]);
}
int main()
{
    int i,j,a,b,c;
    while(scanf("%d%d",&n,&m)!=EOF&&(n!=0||m!=0))
    {
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                if(j==i) road[i][j]=0;
                else road[i][j]=INF;
        for(i=1;i<=m;i++){
            scanf("%d%d%d",&a,&b,&c);
            road[a][b]=c;
            road[b][a]=c;
        }
        Dijkstra(1);
    }
    return 0;
}