栈和队列专题

声明：部分试题、解决方案来自LeetCode，本文旨在学习

1.Valid Parentheses

Given a string containing just the characters ‘(‘, ‘)’, ‘{‘, ‘}’, ‘[’ and ‘]’, determine if the input string is valid.

The brackets must close in the correct order, “()” and “()[]{}” are all valid but “(]” and “([)]” are not.

Solution：

时间复杂度O（n），空间复杂度O（n）

bool isValid(string const& s)
{
    string left = "([{";
    string right = ")]}";
    stack<char> stk;

    for (int i = 0; i < s.size(); i++)
    {
        char c = s[i];
        if(left.find(c) != string::npos)
            stk.push(c);
        else
        {
            if(stk.empty() || stk.top() != left[right.find(c)])
                return false;
            else
                stk.pop();
        }
    }

    return stk.empty();
}

2.Longest Valid Parentheses

Given a string containing just the characters ‘(’ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.

For “(()”, the longest valid parentheses substring is “()”, which has length = 2.

Another example is “)()())”, where the longest valid parentheses substring is “()()”, which has length = 4.

Solution：

时间复杂度O（n），空间复杂度O（n）

int longestValidPaarentheses(string s)
{
    int max_len = 0;
    int last = -1;      //the position of the last ')'
    stack<int> lefts;   //keep track of the positions of non-matching '('s

    for (int i = 0; i < s.size(); i++)
    {
        if(s[i] == '(')
            lefts.push(i);
        else
        {
            if(lefts.empty())
                last = i;  //no matching left
            else
            {
                //find a matching pair
                lefts.pop();
                if(lefts.empty())
                    max_len = max(max_len,i-last);
                else
                    max_len = max(max_len,i-lefts.top());
            }
        }
    }

    return max_len;
}

3. Largest Rectangle in Histogram

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

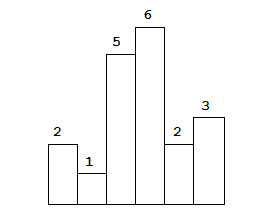
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

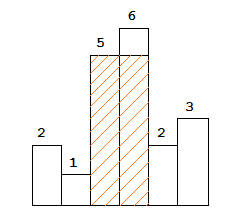
The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given heights = [2,1,5,6,2,3],
return 10.

分析：

如上图，从左向右处理直方，当i=4时，小于当前栈顶（即直方3），对于直方3，无论后面还是前面的直方，都不能得到比目前栈顶元素更高的高度了，处理掉直方3（计算从直方3到直方4之间的举行的面积，然后从栈里弹出）；对于直方2也是如此；直到碰到比直方4更矮的直方1.

这就意味着，可以维护一个递增的栈，每次比较栈顶与当前元素。如果当前元素大于栈顶元素，则入栈，直至栈顶元素小于当前元素。结尾时入栈元素0，重复合并一次。

Solution：

时间复杂度O（n），空间复杂度O（n）

int largestRectangleArea(vector<int> &height)
{
    stack<int> s;
    height.push_back(0); //结尾入栈元素为0
    int result = 0;
    int i = 0;

    while(i < height.size())
    {
        if(s.empty() || height[i] > height[s.top()])
            s.push(i++);
        else
        {
            int tmp = s.top();
            s.pop();
            result = max(result,height[tmp]*(s.empty() ? i : i-s.top()-1));
        }
    }

    return result;
}

下面是二叉树非递归遍历，包括分层层次遍历，非递归先序、中序、后序遍历。先放一张图，是结果截图。

由于主要用到的是栈和队列，故放在本专题

4.层次遍历分层打印

层次遍历用到了队列这一数据结构，分层打印则需要记录当前层和下一层需要打印的个数。

void split_hierarchy_order(Node* root)
{
    queue<Node*> q;
    Node* p;
    q.push(root);
    int cur_hierarchry_count = 1;
    int next_hierarchy_count = 0;

    while(!q.empty())
    {
        if(cur_hierarchry_count > 0)
        {
            p = q.front();
            q.pop();
            if(p != NULL)
                cout << p->val << " ";
            else
                cout << "#" << " ";

            cur_hierarchry_count--;

            if(p != NULL  && (p->left != NULL || p->right != NULL))  //这里运行了C++的判断机制：一旦p != NULL不成立，由于后面的 && 操作符就不继续判断了，从而p->left不会报错
            {
                q.push(p->left);
                next_hierarchy_count++;

                q.push(p->right);
                next_hierarchy_count++;
            }
        }
        else
        {
            cout << endl;
            cur_hierarchry_count = next_hierarchy_count;
            next_hierarchy_count = 0;
        }
    }
}

下面的先序、中序、后序遍历的非递归遍历都需要用到栈这一数据结构

5.非递归先序遍历

void inrecur_pre_order(Node* root)
{
    stack<Node*> s;
    Node* p = root;

    while (!s.empty() || p != NULL)
    {
        while(p != NULL)
        {
            cout << p->val << " ";
            s.push(p);
            p = p->left;
        }
        if (!s.empty())
        {
            p = s.top();
            p = p->right;
            s.pop();
        }
    }
}

6.非递归中序遍历

非递归中序遍历与先序遍历思路基本差不多，对于何时打印节点的值稍微考虑一下就行了。

void inrecur_in_order(Node* root)
{
    stack<Node*> s;
    Node* p = root;

    while (!s.empty() || p != NULL)
    {
        while (p != NULL)
        {
            s.push(p);
            p = p->left;
        }
        if (!s.empty())
        {
            p = s.top();
            cout << p->val << " ";
            s.pop();
            p = p->right;
        }
    }
}

7.非递归后序遍历

非递归后续遍历应该是非递归遍历中最难的了，为了方便理解思路。我们需要在数据结构做些改动。

struct Node{
    int val;
    Node* left;
    Node* right;
    bool isFirst;  //用于记录节点是否是第一次被访问
    Node(int value,Node* l = NULL,Node* r = NULL,bool isF = false):val(value),left(l),right(r),isFirst(isF){};
};

根据非递归后续遍历的任务，我们可以理解为在节点第二次被访问时进行输出。

void inrecur_post_order(Node* root)
{
    stack<Node*> s;
    Node* p = root;

    while (p != NULL || !s.empty())
    {
        while (p != NULL)
        {
            s.push(p);
            p->isFirst = true;
            p = p->left;
        }
        if (!s.empty())
        {
            p = s.top();
            s.pop();

            if (p->isFirst == true)    //第一次出现在栈顶
            {
                s.push(p);
                p->isFirst = false;
                p = p->right;
            }
            else       //第二次出现在栈顶
            {
                cout << p->val << " ";
                p = NULL;   //很重要
            }
        }
    }
}