学习笔记（八）：FingerDraw与WiFi手势追踪

2020《FingerDraw: Sub-wavelength Level Finger Motion Tracking with WiFi Signals》读书笔记

  本文基于基于感知微小运动的CSI商模型和指画分割与重建技术，实现误差为1.27cm的任意二维手势绘制。如图（1）所示：

1. WiFi手势识别现状

  WiFi手势识别大致可分为基于模式识别方法（如Mudra、Widar3.0）和基于运动追踪方法的两类（如Qgesture、GingerDraw）。

模式识别仅能识别预定义的手势集，不能进行任意的手指运动跟踪。

现有的基于运动追踪的方法有如下缺点:
① 受到原始CSI振幅中的噪声的影响，并且在提取的多普勒速度分布中呈现低信噪比，导致定位的粗粒度。用共轭相乘法有幅度噪声。
② 要求目标移动至少几个波长，以便正确提取运动信息。

2. 现有方法不能感知亚波长级手指运动的原因

2.1和2.2说明了为什么利用原始CSI信号和模式识别方法精确度不够
2.3说明QGesture的方法的缺陷

2.1 手指运动和CSI信号变化之间在菲涅耳区背景下的映射

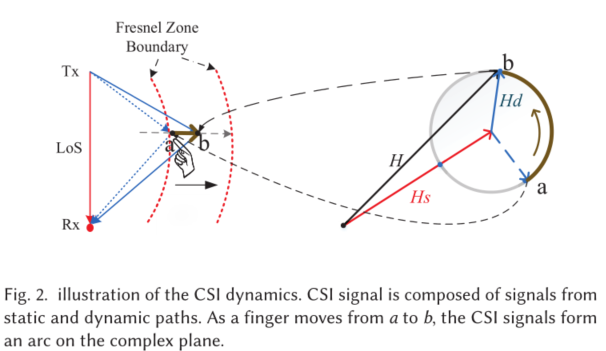
  图2中，手指在一对WiFi收发器的感应范围内移动。接收信号强度是来自静态视线(LoS)传播和环境反射的所有路径分量以及手指的动态反射路径的叠加。波长$\lambda$的信号，反射径长度变化$d$，动态反射路径就会有$2\pi d/\lambda$的相移。

CSI模型：
$$H(f,t)=H_s(f,t)+H_d(f,t)=H_s(f,t)+A(f,t)e^{-j2\pi \frac{d(t)}{\lambda }}$$  当手指移动时，反射路径改变其长度，动态相量$H_d(f,t)$分量相应旋转。如果反射路径的长度变化小于一个波长，则叠加的CSI沿圆弧变化。动态分量的旋转方向与手指的运动方向相关，能反映出反射路径的长度增加或减少。
  当一个物体穿过一系列菲涅耳区时，接收信号显示出连续的类似正弦波的波形。如果由移动物体引起的反射路径长度变化短于一个波长，则接收信号只是正弦状波形的一个片段。
  对于类似的手指运动，CSI波形图样可能会有所不同，这取决于手指在绘图时移动穿过多少个菲涅耳区，以及菲涅耳区中的初始位置。

2.2 实验验证相似手势CSI波形的巨大差异

  控制变量法：图3（1）和图三（2）位置相同，字母d大小不同，图三（2）和图三（3）初始位置不同，字母d大小相同。

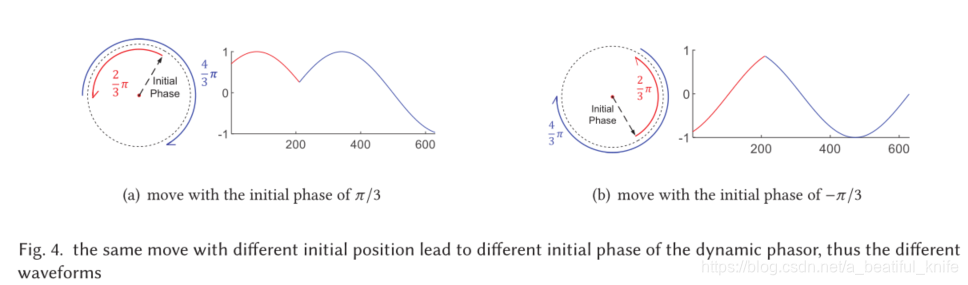
  图四是理论仿真。

2.3 Qgesture方法的缺陷

  2018《QGesture: Quantifying Gesture Distance and Direction with WiFi Signals.》
  Qgesture中估计静态分量的方法是在滑动窗口上平均CSI数据，所以手势轨迹精度不够。

3. 基于CSI商的手势追踪

3.1 CSI商模型优点

1)消除了原始CSI信号中的大部分噪声，更有利于监测微小的手指运动
2)提供了完全可用的复数值的相位和振幅信息，保持了运动位移和CSI信号之间的相关性（复平面的轨迹能反映运动特征）

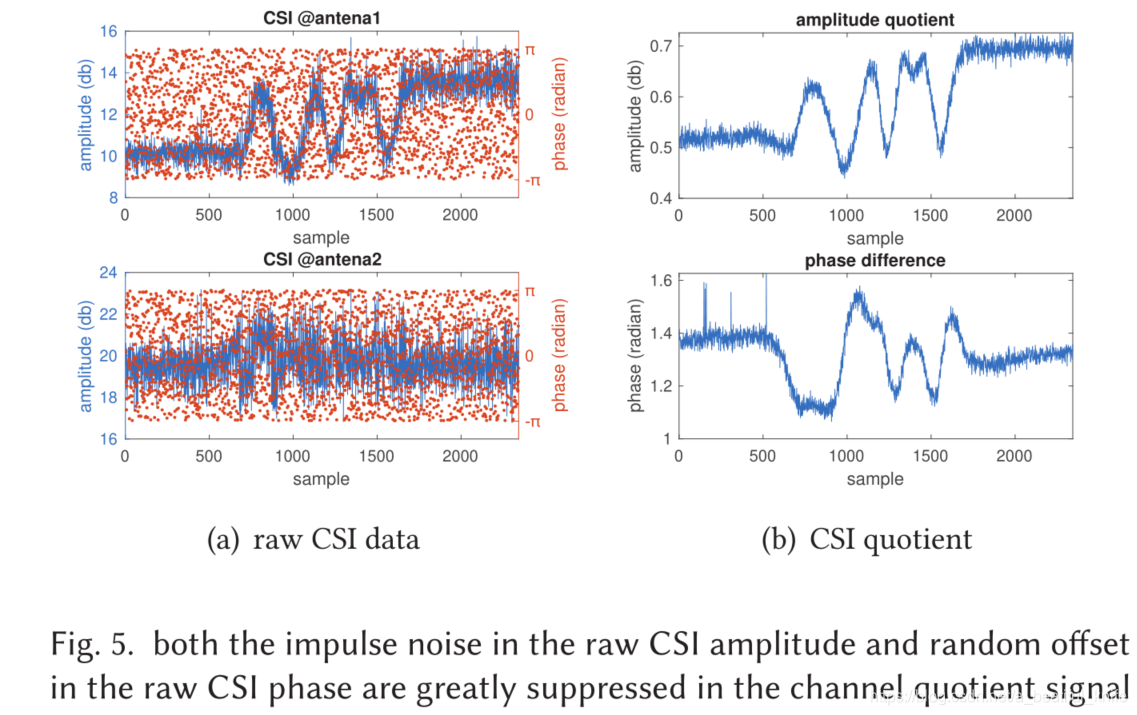
  图5显示了原始CSI和CSI商。在图5(a)中，CSI相位的样本(红点)随机分布在所有天线的[−$\pi$,$\pi$]中，并且观察到振幅中有严重脉冲噪声（蓝线）。CSI商中，幅度和相位上去除大部分噪声。

3.2 CSI商模型（和Farsense一模一样，就当复习）

  假设两个固定位置有一对收发器和一个移动目标（如手指），如图（1）所示。LoS和反射环境静态物体的信号组合成静态信号分量，手指反射构成动态信号分量，CSI商的形式为:
H q ( f , t ) = A n o i s e ( f , t ) e − j θ o f f s e t ( f , t ) ( H s 1 ( f , t ) + H d 1 ( f , t ) ) A n o i s e ( f , t ) e − j θ o f f s e t ( f , t ) ( H s 2 ( f , t ) + H d 2 ( f , t ) ) = H s 1 ( f , t ) + H d 1 ( f , t ) H s 2 ( f , t ) + H d 2 ( f , t ) H_{q}(f, t)=\frac{A_{n o i s e}(f, t) e^{-j \theta_{o f f s e t}(f, t)}\left(H_{s 1}(f, t)+H_{d 1}(f, t)\right)}{A_{n o i s e}(f, t) e^{-j \theta_{o f f s e t}(f, t)}\left(H_{s 2}(f, t)+H_{d 2}(f, t)\right)}=\frac{H_{s 1}(f, t)+H_{d 1}(f, t)}{H_{s 2}(f, t)+H_{d 2}(f, t)} H