BCH码（能纠正多个随机错误的循环码）

PS：课上讲的也是编解码流程，也没有原理，网上也没找到每一步的原理，想要了解设计思路还是需要去找一下原版的论文。

参考blog：
【1】【举例子详细分析】BCH码(BCH code)

1. 伽罗华域和多项式

  见之前的blog伽罗华域GF

2. 提出背景和思路

  奇偶校验码只能检查出错误而不知道具体是哪里出错。
  hamming码只能纠正 1 bit 错误。
  在GF$(2^q)$中，用多项式表示对应的有限域中的数值，多项式又可表示成二进制bit流的形式，等于二进制bit流与符号之间的一一映射，同时二进制多项式加法和二进制的按位异或等同（二进制流所受的干扰可用加法表示），多项式乘法及其逆运算能够实现多项式的恢复，本原多项式能保证逆运算结果具有唯一性。

  现假设待传输的消息用二进制流对应的$m(x)$表示，乘上一个编码多项式$p(x)$，传输过程收到干扰可表示为$e(x)$，则接受到：$$c(x)=m(x)p(x)+e(x)$$如果接受端也知道p(x)，那么就能得到$m(x)$和$e(x)$。

本原元→本原多项式：

1. GF$(2^q)$上的本原元是一个元素, 在域中的任何非零元素都可以表示为它的方幂
2. 任意一个有限域 GF$(2^q)$必有一个本原元$\alpha$
3. 本原元的阶数为$2^q-1$，即${\alpha }^{2^q-1}+1=0$
4. 本原多项式$p(x)$是以本原元$\alpha$为根的、首项系数为1的最低阶不可约多项式

3. 案例：为什么需要本原多项式

对于GF$(2^4)$，有本原多项式$p(x)=x^2+x+1$
  $m(x)$是$1001$，而编码多项式$p(x)$是$1101$，则$m(x)\ast p(x)=1100101$。若收到了干扰$e(x)=0000010$，则接受到$1100111$,

e(x)	e(x)/p(x) 的余项
1000000	1000000
0100000	0100000
0010000	0010000
0001000	1100000
0000100	0110000
0000010	1110000
0000001	1010000

  从表中可看出，$e(x)$和所得余项一一对应，通过余项结果可找到对应的$e(x)$。如果采用$p(x)=10001=101\ast 101$，1000000和0000100除以10001后余项均为1000000。

4. BCH码编码过程

  思想：一个本原多项式纠正一个错误，通过修正编码多项式$$c(x)=m(x)Q(x)+e(x)$$令其中$Q(x)=p(x)p_3(x)p_5(x)\cdots p_{2t-1}(x)$，p(x)是本原多项式，实现纠正多个错误。

  $p_{2t-1}(x)$的性质(a mod b=c，表明a除以b余数为c):

1. $p_{2i-1}(x)modp(x)=0，i=2,...,t$
2. 本原BCH码$p(\alpha )=p({\alpha }^3)=...=p({\alpha }^{2t-1})=0$

  以$n=2^4-1=15$, 纠错数量$t=3$ 的本原BCH码为例，设$\alpha$为GF$(2^4)$的本原元，本原多项式为$p(x)=x^4+x+1$，那么$Q(x)=p(x)p_3(x)p_5(x)$，现有$p(x)=x^4+x+1=(x-\alpha )(x-{\alpha }^2)(x-{\alpha }^4)(x-{\alpha }^8)$，画表得到其共轭根为${\alpha }^3,{\alpha }^6,{\alpha }^{12},{\alpha }^9$，故$p_3(x)=(x-{\alpha }^3)\left(x-{\alpha }^6\right)\left(x-{\alpha }^2\right)\left(x-{\alpha }^9\right)=x^4+x^3+x^2+x+1$，剩余两根构成$p_5(x)=\left(x-{\alpha }^5\right)\left(x-{\alpha }^{10}\right)=x^2+x+1$。此时$g(x)=p(x)p_3(x)p_5(x)=x^{10}+x^8+x^5+x^4+x^2+x+1$。

此时n=15，t=3，deg（g(x)）= 10, k=n-deg=5，t=3，设计的码距d=2t+1，实际码距和设计码距相等

PS：（以上推导过程为法一，适合做题不适合编程）
法二：上图中极小多项式是$x^{2^q-1}$的因式分解结果，一个BCH码的生成多项式也可由$LCM[f_1(x),f_2(x),\dots ,f_{2t}(x)]$给出，详细可见参考文献【1】

5. BCH码译码过程

由于$m(x)Q(x)$以${\alpha }^1,{\alpha }^2,\dots ,{\alpha }^{2t}$为根。想要知道错误图样，需要知道在位置i是否发生错误。
定义$e(x)={\sum }_{i=0}^{n-1}{e}_i{x}^i={\sum }_{l=1}^{\gamma }{Y}_l{x}^{i_l}$，$i_l$表示错误位置。
译码五步：

5.1 伴随多项式的计算
法一：接收端知道$Q(x)$，能得到对应的$h(x)=\frac{x^n+1}{Q(x)}$，从而写出H，即可计算s（x）
法二：

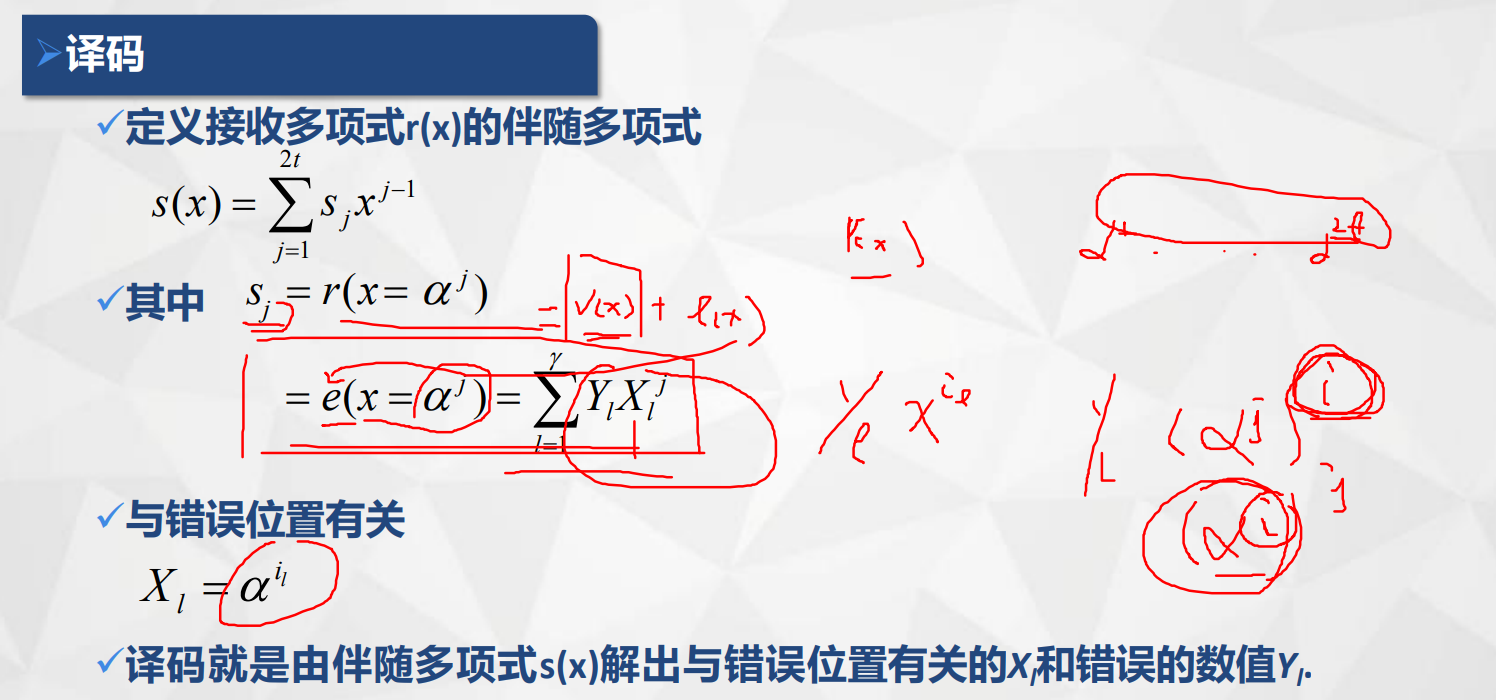
推导过程：

5.2 错误位置多项式系数的求解：

5.3 错误位置的确定

5.4 计算对应错误位置上的错误数值

5.5 得到e（x），输出结果