矩阵，简单的运行技巧

对于矩阵乘法 C =  A× B，通常的做法是将矩阵进行分块相乘，如下图所示：

 

 

 

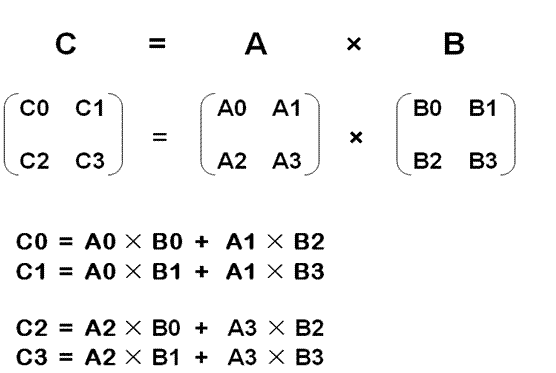
从上图可以看出这种分块相乘总共用了8次乘法，当然对于子矩阵相乘（如A0×B0），还可以继续递归使用分块相乘。对于中小矩阵来说，很适合使用这种分块乘法，但是对于大矩阵来说，递归的次数较多，如果能减少每次分块乘法的次数，那么性能将可以得到很好的提高。

Strassen矩阵乘法就是采用了一个简单的运算技巧，将上面的8次矩阵相乘变成了7次乘法，看别小看这减少的1次乘法，因为每递归1次，性能就提高了1/8，比如对于1024*1024的矩阵，第1次先分解成7次512*512的矩阵相乘，对于512*512的矩阵，又可以继续递归分解成256*256的矩阵相乘，…，一直递归下去，假设分解到64*64的矩阵大小后就不再递归，那么所花的时间将是分块矩阵乘法的(7/8) * (7/8) * (7/8) * (7/8) = 0.586倍，提高了快接近一倍。当然这是理论上的值，因为实际上strassen乘法增加了其他运算开销，实际性能会略低一点。

下面就是Strassen矩阵乘法的实现方法，

   M1 = (A0 + A3) × (B0 + B3)

   M2 = (A2 + A3) × B0

   M3 = A0 × (B1 - B3)

   M4 = A3 × (B2 - B0)

   M5 = (A0 + A1) × B3

   M6 = (A2 - A0) × (B0 + B1)

   M7 = (A1 - A3) × (B2 + B3)

   C0 = M1 + M4 - M5 + M7

   C1 = M3 + M5

   C2 = M2 + M4

   C3 = M1 - M2 + M3 + M6

在求解M1,M2,M3,M4,M5,M6,M7时需要使用7次矩阵乘法，其他都是矩阵加法和减法。

下面看看Strassen矩阵乘法的串行实现伪代码：

Serial_StrassenMultiply(A, B, C) 

{

   T1 = A0 + A3;

   T2 = B0 + B3;

   StrassenMultiply(T1, T2, M1);

   T1 = A2 + A3;

   StrassenMultiply(T1, B0, M2);

   T1 = (B1 - B3);

   StrassenMultiply (A0, T1, M3);

 

   T1 = B2 - B0;

   StrassenMultiply(A3, T1, M4);

 

   T1 = A0 + A1;

   StrassenMultiply(T1, B3, M5);       

   

   T1 = A2 – A0;

   T2 = B0 + B1;

   StrassenMultiply(T1, T2, M6);

   T1 = A1 – A3;

   T2 = B2 + B3;

   StrassenMultiply(T1, T2, M7);

   C0 = M1 + M4 - M5 + M7

   C1 = M3 + M5

   C2 = M2 + M4

   C3 = M1 - M2 + M3 + M6

}

本文转载自http://software.intel.com/zh-cn/blogs/2009/12/08/400002843/?cid=sw:prccsdn893