2014年蓝桥杯的第九题是这样描述的:
给定Fibonacci数列F[],其中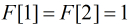
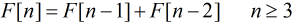
的值。其中
在讲解这道题之前,我们先来看一个简单版的。题目如下:
题目:http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1194
分析:可以看出本题就是直接求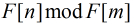
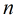
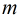
在Fibonacci数列中有很多有用的性质,比如:
实际上,这个两个公式的推导过程也比较简单。(两种证明方法:带入公式验证;数学归纳法)
所以,我们可以这样来把原表达式变形,即:
那么,我们继续对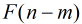
可以看出,到了这一步,我们就把所有的Fibonacci数列的下标减小了,基本可以直接计算了。
因为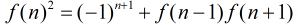
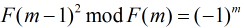
所以到了这里,本题基本就说完了,只需要预处理前1000个Fibonacci数列即可。代码如下:
import java.io.*;
import java.util.*;
import java.math.BigInteger;
public class Main {
final static int N = 1005;
static BigInteger F[] = new BigInteger[N];
static void Init(){
F[0] = BigInteger.ZERO;
F[1] = BigInteger.ONE;
for(int i=2;i<N;i++)
F[i] = F[i-1].add(F[i-2]);
}
public static void main(String[] args){
Init();
Scanner cin = new Scanner(System.in);
int T = cin.nextInt();
while(T-- != 0){
long n = cin.nextLong();
int k = cin.nextInt();
int x = (int)(n % k);
long y = n / k;
int sign = 1;
if((k & 1) == 1)
sign = -1;
BigInteger ans = F[x];
if(sign == 1){
if((y & 1L) == 1L)
ans = ans.multiply(F[k-1]);
}
else{
if((y & 1L) == 1L)
ans = ans.multiply(F[k-1]);
y >>= 1;
if((y & 1L) == 1L)
ans = ans.multiply(F[k].subtract(BigInteger.ONE));
}
System.out.println(ans.mod(F[k]));
}
}
}
完美解出上题后,我们来看2014年蓝桥杯的C++ A组的第九题,题目描述在文章开始处。
可以看出本题的难点在于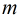
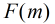
因为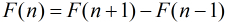
所以我们可以把原问题简单模型化为求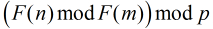
经过上面简单版题目的介绍,我们知道
又知道
那么分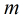
一.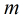
很明显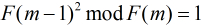
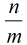
(1)如果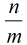
(2)如果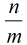
二.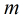
得到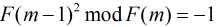
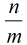
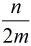
(1)如果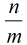
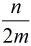
(2)如果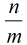
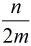
(3)如果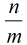
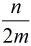
(4)如果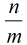
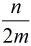
从上面的所有情况来看,难点就在于如何进一步简化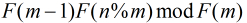
对于这个问题,我们还有另一个性质
性质:若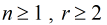
可以看出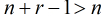
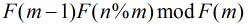
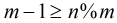
我们令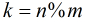
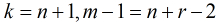
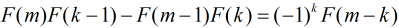
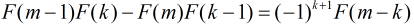
可以看出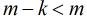
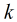
(1)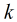
(2)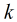
到了这里,我们就对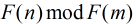
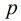
最后,来看一道类似的题目。描述如下
题目:http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1365
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N = 2;
const int MOD = 1000000007;
struct Matrix
{
LL m[N][N];
};
Matrix I = {
1, 0,
0, 1
};
Matrix A = {
1, 1,
1, 0
};
Matrix multi(Matrix A, Matrix B)
{
Matrix C;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N; j++)
{
C.m[i][j] = 0;
for(int k = 0; k < N; k++)
C.m[i][j] += A.m[i][k] * B.m[k][j];
C.m[i][j] %= MOD;
}
}
return C;
}
Matrix Power(Matrix A, LL n)
{
Matrix ans = I, P = A;
while(n)
{
if(n & 1)
{
ans = multi(ans, P);
n--;
}
n >>= 1;
P = multi(P, P);
}
return ans;
}
//计算F(n) % MOD
LL getFun(LL n)
{
Matrix ans = Power(A, n);
return ans.m[1][0];
}
//计算F(m - 1) * F(n % m) mod F(m)
LL getRes(LL n, LL m)
{
LL k = n % m;
if(k & 1)
return getFun(m - k);
return ((getFun(m) - getFun(m - k)) % MOD + MOD) % MOD;
}
LL Solve(LL n, LL m)
{
LL t1 = n / m;
if(m & 1)
{
LL t2 = t1 >> 1;
if(t1 % 2 == 0 && t2 % 2 == 0)
return getFun(n % m);
if(t1 % 2 == 0 && t2 % 2 == 1)
return ((getFun(m) - getFun(n % m)) % MOD + MOD) % MOD;
if(t1 % 2 == 1 && t2 % 2 == 0)
return getRes(n, m);
if(t1 % 2 == 1 && t2 % 2 == 1)
return ((getFun(m) - getRes(n, m)) % MOD + MOD) % MOD;
}
else
{
if(t1 & 1)
return getRes(n, m);
else
return getFun(n % m);
}
}
LL getResponse(LL n, LL m)
{
// n += 2;
LL res = Solve(n, m);
// if(res == 0)
// return getFun(m) - 1;
// return res - 1;
return res;
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
LL n, k;
scanf("%lld %lld", &n, &k);
printf("%lld\n", getResponse(n, k));
}
return 0;
}








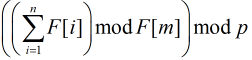

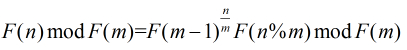
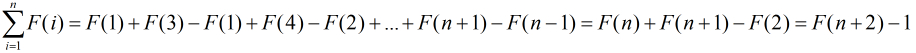
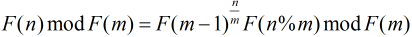
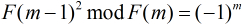
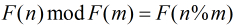
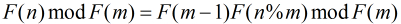
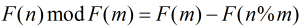
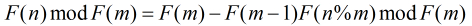
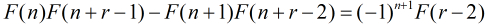
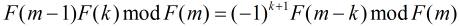
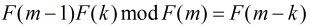
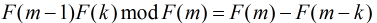














 581
581











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








